Skip to main content
SpringerLink
Log in

Rational and semi-rational solutions of a (3+1)-dimensional generalized Calogero–Bogoyavlenskii–Schiff equation

  • Original Paper
  • Published:
Nonlinear Dynamics Aims and scope Submit manuscript

Abstract

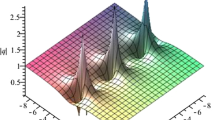
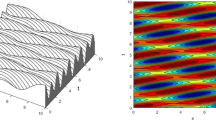
This paper mainly focuses on a (3+1)-dimensional generalized Calogero–Bogoyavlenskii–Schiff equation which provides overwhelming support for studying the dynamics of high-dimensional nonlinear wave equations. The bilinear form of the equation is obtained based on the Hirota bilinear method, and the N-soliton solutions composed of the higher-order breather, periodic line wave and the mixed forms are constructed. Then, the rational and semi-rational solutions of the equation were acquired by using complex conjugate parameter relations and the long-wave limit method, which mainly consisted of high-order solitons, lumps, breathers and their mixed forms. We analyze the effect of the coefficients of space and time variables on the interaction of solutions to bilinear equations. By classifying these coefficients, we find that these coefficients change the interaction of the solutions by affecting the velocity, position, and trajectory of the waves. In order to describe the dynamics of solutions with different parameters more directly, the time evolution plots and density plots are presented, and the appearance and movement characteristics of the solutions are analyzed.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17

Similar content being viewed by others

Data availability

Data sharing is not applicable to this article as no new data were created or analyzed in this paper.

References

  1. Bang, O., Peyrard, M.: High order breather solutions to a discrete nonlinear Klein–Gordon model. Phys. D 81, 9–22 (1995)

    MATH  Google Scholar 

  2. Panayotaros, P.: Breather solutions in the diffraction managed NLS equation. Phys. D 206, 213–231 (2005)

    MathSciNet  MATH  Google Scholar 

  3. Wang, L., Yan, Z.Y., Guo, B.L.: Numerical analysis of the Hirota equation: modulational instability, breathers, rogue waves, and interactions. Chaos 30, 013114 (2020)

    MathSciNet  MATH  Google Scholar 

  4. Xu, G., Gelash, A., Chabchoub, A., Zakharov, V., Kibler, B.: Breather wave molecules. Phys. Rev. Lett. 122, 084101 (2019)

    Google Scholar 

  5. Gilson, C.R., Nimmo, J.J.C.: Lump solutions of the BKP equation. Phys. Lett. A 147, 472–476 (1990)

    MathSciNet  Google Scholar 

  6. Ma, W.X.: Lump solutions to the Kadomtsev–Petviashvili equation. Phys. Lett. A 379, 1975–1978 (2015)

    MathSciNet  MATH  Google Scholar 

  7. Mao, J.J., Tian, S.F., Zou, L., Zhang, T.T., Yan, X.J.: Bilinear formalism, lump solution, lumpoff and instanton/rogue wave solution of a (3+1)-dimensional B-type Kadomtsev–Petviashvili equation. Nonlinear Dyn. 95, 3005–3017 (2019)

    MATH  Google Scholar 

  8. Liu, T.S., Xia, T.C.: \(N\)-soliton, breathers, lumps and interaction solutions for a time-variable coefficients integrable equation in Kadomtsev–Petviashvili hierarchy. Nonlinear Dyn. 111, 11481–11495 (2023)

    Google Scholar 

  9. Solli, D.R., Ropers, C., Koonath, P., Jalali, B.: Optical rogue waves. Nature 450, 1054–1057 (2007)

    Google Scholar 

  10. Zhang, X.E., Chen, Y.: Rogue wave and a pair of resonance stripe solitons to a reduced (3+1)-dimensional Jimbo–Miwa equation. Commun. Nonlinear Sci. 52, 24–31 (2017)

    MathSciNet  MATH  Google Scholar 

  11. Chen, L., Zhu, H.P.: Partially nonlocal bright-dark rogue waves and bright-bright rogue wave pairs of a vector nonlinear schrödinger equation. Nonlinear Dyn. 111, 7699–7711 (2023)

    Google Scholar 

  12. Yang, B., Yang, J.K.: Rogue waves in the nonlocal PT-symmetric nonlinear schrödinger equation. Lett. Math. Phys. 109, 945–973 (2019)

    MathSciNet  MATH  Google Scholar 

  13. Guo, B.L., Ling, L.M.: Rogue wave, breathers and Bright-Dark-Rogue solutions for the coupled schrödinger equations. Chinese Phys. Lett. 28, 110202 (2011)

    Google Scholar 

  14. Osman, M.S., Wazwaz, A.M.: An efficient algorithm to construct multi-soliton rational solutions of the (2+1)-dimensional KdV equation with variable coefficients. Appl. Math. Comput. 321, 282–289 (2018)

    MathSciNet  MATH  Google Scholar 

  15. Osman, M.S.: Analytical study of rational and double-soliton rational solutions governed by the KdV-Sawada-Kotera-Ramani equation with variable coefficients. Nonlinear Dyn. 89, 2283–2289 (2017)

    MathSciNet  Google Scholar 

  16. Yan, Z.Y.: Abundant new multiple soliton-like solutions and rational solutions of the (2+1)-dimensional Broer–Kaup equation. Z. Naturforsch. A 56, 816–824 (2001)

    Google Scholar 

  17. Zhang, R.F., Li, M.C., Gan, J.Y., Li, Qing, Lan, Z.Z.: Novel trial functions and rogue waves of generalized breaking soliton equation via bilinear neural network method. Chaos Soliton. Fract. textbf154, 111692 (2022)

  18. Zhang, R.F., Li, M.C., Albishari, M., Zheng, F.C., Lan, Z.Z.: Generalized lump solutions, classical lump solutions and rogue waves of the (2+1)-dimensional Caudrey-Dodd-Gibbon-Kotera-Sawada-like equation. Appl. Math. Comput. 403, 126201 (2021)

    MathSciNet  MATH  Google Scholar 

  19. Boccato, C., Brennecke, C., Cenatiempo, S., Schlein, B.: Complete Bose–Einstein condensation in the Gross–Pitaevskii regime. Commun. Math. Phys. 359, 975–1026 (2018)

    MathSciNet  MATH  Google Scholar 

  20. Cao, Y.L., Malomed, B.A., He, J.S.: Two (2+1)-dimensional integrable nonlocal nonlinear schrödinger equations: breather, rational and semi-rational solutions. Chaos Soliton Fract. 114, 99–107 (2018)

    MATH  Google Scholar 

  21. Wang, S.N., Yu, G.F.: Rational and semi-rational solutions to the Davey–Stewartson III equation. Nonlinear Dyn. 111, 7635–7655 (2023)

    Google Scholar 

  22. Liu, W., Wazwaz, A.M., Zheng, X.X.: Families of semi-rational solutions to the Kadomtsev–Petviashvili I equation. Commun. Nonlinear Sci. 67, 480–491 (2019)

    MathSciNet  MATH  Google Scholar 

  23. Liu, W., Wazwaz, A.M., Zheng, X.X.: High-order breathers, lumps, and semi-rational solutions to the (2+1)-dimensional Hirota–Satsuma–Ito equation. Phys. Scr. 94, 75203 (2019)

    Google Scholar 

  24. Yang, Y.M., Xia, T.C., Liu, T.S.: Darboux transformation and exact solution to the nonlocal Kundu–Eckhaus equation. Appl. Math. Lett. 141, 108602 (2023)

    MathSciNet  MATH  Google Scholar 

  25. Zayed, E.M.E., Al-Nowehy, A.G.: Exact solutions and optical soliton solutions for the (2+1)-dimensional hyperbolic nonlinear schrödinger equation. Optik 127, 4970–4983 (2016)

    Google Scholar 

  26. Wazwaz, A.M.: New (3+1)-dimensional painlev\(\acute{\rm {e}}\) integrable fifth-order equation with third-order temporal dispersion. Nonlinear Dyn. 106, 891–897 (2021)

    Google Scholar 

  27. Yao, J., Lesage, A.C., Bodmann, B.G., Hussain, F., Kouri, D.J.: Inverse scattering theory: inverse scattering series method for one dimensional non-compact support potential. J. Math. Phys. 55, 123512 (2014)

    MathSciNet  MATH  Google Scholar 

  28. Ablowitz, M.J., Harvey, S.: Solitons and the inverse scattering transform. Philadelphia: SIAM v.4 (1981)

  29. Constantin, A., Gerdjikov, V.S., Ivanov, R.I.: Inverse scattering transform for the Camassa-Holm equation. Inverse Probl. 22, 2197–2207 (2006)

    MathSciNet  MATH  Google Scholar 

  30. Matveev, V.B., Salle, M.A.: Darboux Transformations and Solitons. Springer-Verlag, Berlin (1991)

    MATH  Google Scholar 

  31. Li, J., Xia, T.C.: Darboux transformation to the nonlocal complex short pulse equation. Appl. Math. Lett. 126, 107809 (2022)

    MathSciNet  MATH  Google Scholar 

  32. Zhang, N., Xia, T.C., Jin, Q.Y.: \(N\)-fold darboux transformation of the discrete Ragnisco-Tu system. Adv. Differ. Equ-Ny. 2018, 1–10 (2018)

    MATH  Google Scholar 

  33. Shen, Y., Tian, B.: Bilinear auto-Bäcklund transformations and soliton solutions of a (3+1)-dimensional generalized nonlinear evolution equation for the shallow water waves. Appl. Math. Lett. 122, 107301 (2021)

    MATH  Google Scholar 

  34. Xin, X.P., Xia, Y.R., Zhang, L.H., Liu, H.Z.: Bäcklund transformations, symmetry reductions and exact solutions of (2+1)-dimensional nonlocal DS equations. Appl. Math. Lett. 132, 108157 (2022)

    MATH  Google Scholar 

  35. Batool, N., Masood, W., Siddiq, M., Alrowaily, A.W., Ismaeel, S.M.E., Melville, S.A.: Hirota bilinear method and multi-soliton interaction of electrostatic waves driven by cubic nonlinearity in pair-ion-electron plasmas. Phys. Fluids 35, 33109 (2023)

    Google Scholar 

  36. Alquran, M., Alhami, R.: Analysis of lumps, single-stripe, breather-wave, and two-wave solutions to the generalized Perturbed–KdV equation by means of Hirota’s bilinear method. Nonlinear Dyn. 109, 1985–1992 (2022)

    Google Scholar 

  37. Zhang, R.F., Li, M.C.: Bilinear residual network method for solving the exactly explicit solutions of nonlinear evolution equations. Nonlinear Dyn. 108, 521–531 (2022)

    Google Scholar 

  38. Zhang, R.F., Bilige, S.: Bilinear neural network method to obtain the exact analytical solutions of nonlinear partial differential equations and its application to P-gBKP equation. Nonlinear Dyn. 95, 3041–3048 (2019)

    MATH  Google Scholar 

  39. Liu, T.S., Xia, T.C.: Riemann–Hilbert problems and \(N\)-soliton solutions of the nonlocal reverse space-time Chen–Lee–Liu equation. Commun. Theor. Phys. 75, 35002 (2023)

    MathSciNet  Google Scholar 

  40. Malik, A., Chand, F., Kumar, H., Mishra, S.C.: Exact solutions of the Bogoyavlenskii equation using the multiple \({\rm {(G^{^{\prime }}/G)}}\)-expansion method. Comput. Math. Appl. 64, 2850–2859 (2012)

    MathSciNet  MATH  Google Scholar 

  41. Huang, L.L., Chen, Y.: Nonlocal symmetry and similarity reductions for a (2+1)-dimensional Korteweg–de Vries equation. Nonlinear Dyn. 92, 221–234 (2018)

    MATH  Google Scholar 

  42. Yan, Z.Y.: Numerical doubly periodic solution of the KdV equation with the initial condition via the decomposition method. Appl. Math. Comput. 168, 1065–1078 (2005)

    MathSciNet  MATH  Google Scholar 

  43. Hu, B.B., Xia, T.C., Zhang, N.: The unified transform method to initial-boundary value problem for a coupled cubic-quintic nonlinear schrödinger system. Complex Anal. Oper. Th. 13, 1143–1159 (2019)

    MATH  Google Scholar 

  44. Geng, X.G., Li, R.M., Xue, B.: A vector Geng-Li model: new nonlinear phenomena and breathers on periodic background waves. Phys. D 434, 133270 (2022)

    MathSciNet  MATH  Google Scholar 

  45. Liu, C.F., Wang, Z.P., Dai, Z.D., Chen, L.W.: Rogue waves in the (2+1)-dimensional nonlinear schrödinger equations. Int. J. Numer. Method H. 25, 656–664 (2015)

    MATH  Google Scholar 

  46. Ding, C.C., Gao, Y.T., Deng, G.F.: Breather and hybrid solutions for a generalized (3+1)-dimensional B-type Kadomtsev–Petviashvili equation for the water waves. Nonlinear Dyn. 97, 2023–2040 (2019)

    MATH  Google Scholar 

  47. Bogoyavlenskii, O.I.: Overturning solitons in new two dimensional integrable equations. Math. USSR-Izv. 34, 245–260 (1990)

    MathSciNet  Google Scholar 

  48. Schiff, J.: Integrability of Chern–Simons–Higgs Vortex Equations and a Reduction of the Self-Dual Yang-Mills Equations to Three Dimensions. Springer, USA (1992)

    MATH  Google Scholar 

  49. Wazwaz, A.M.: The (2+1) and (3+1)-dimensional CBS equations: multiple soliton solutions and multiple singular soliton solutions. Z. Naturforsch. A. 65, 173–181 (2010)

    Google Scholar 

  50. Zhou, Y., Zhang, X.J., Zhang, C., Jia, J.J., Ma, W.X.: New lump solutions to a (3+1)-dimensional generalized Calogero–Bogoyavlenskii–Schiff equation. Appl. Math. Lett. 141, 108598 (2023)

    MathSciNet  MATH  Google Scholar 

  51. Jadaun, V., Kumar, S.: Lie symmetry analysis and invariant solutions of (3+1)-dimensional Calogero–Bogoyavlenskii–Schiff equation. Nonlinear Dyn. 93, 349–360 (2018)

  52. Satsuma, J., Ablowitz, M.J.: Two-dimensional lumps in nonlinear dispersive systems. J. Math. Phys. 20, 1496–1503 (1979)

    MathSciNet  MATH  Google Scholar 

  53. Guo, H.D., Xia, T.C., Hu, B.B.: High-order lumps, high-order breathers and hybrid solutions for an extended (3+1)-dimensional Jimbo-Miwa equation in fluid dynamics. Nonlinear Dyn. 100, 601–614 (2020)

  54. Liu, Y.K., Li, B., An, H.L.: General high-order breathers, lumps in the (2+1)-dimensional Boussinesq equation. Nonlinear Dyn. 92, 2061–2076 (2018)

    Google Scholar 

Download references

Funding

The authors are grateful to the Editors and the Reviewers for their invaluable comments and suggestions, which have greatly improved the quality of this paper. The work is supported by the National Natural Science Foundation of China under Grant No.11975145.

Author information

Authors and Affiliations

  1. Department of Mathematics, Shanghai University and Newtouch Center for Mathematics of Shanghai University, Shanghai, 200444, China

    Yingmin Yang, Tiecheng Xia & Tongshuai Liu

Authors
  1. Yingmin Yang
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Tiecheng Xia
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Tongshuai Liu
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Tiecheng Xia.

Ethics declarations

Conflict of interest

The authors declare that they have no conflict of interest.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

The work is in part supported by the Natural Science Foundation of China under Grant No. 11975145.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Yang, Y., Xia, T. & Liu, T. Rational and semi-rational solutions of a (3+1)-dimensional generalized Calogero–Bogoyavlenskii–Schiff equation. Nonlinear Dyn 111, 16377–16394 (2023). https://doi.org/10.1007/s11071-023-08682-6

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11071-023-08682-6

Keywords

Mathematics Subject Classification

Search

Navigation