Multiple timing and spatial scaling for bifurcations

Abstract

Scaling time and spatial domains often seem natural in ODEs, but unfortunately, its useful explicit form does not always agree with intuition. After reviewing the well-known methods, multiple timing and averaging, we will show that algebraic timelike variables may play a part in bifurcations. Part of this discussion is tied in with the problem of structural stability in the analysis of matrices, and another part is determined by bifurcation theory of nonlinear systems. Secondly, the theory of resonance manifolds for higher dimensional problems involving at least 2 angles will show the presence of unexpected small spatial domains that may emerge involving long timescales and containing interesting phenomena. A number of examples from mechanics are presented to demonstrate the theory.

1 Introduction

The theme of this paper is to discuss unexpected timelike and spatial variables in differential equations. Consider ordinary differential equations (ODEs) that contain a small positive parameter $\varepsilon$:

$$\begin{aligned} {\dot{x}} = f(t, x, \varepsilon ),\,\,x \in {\mathbb {R}}^n \end{aligned}$$

(1)

depending to some order smoothly on x and t for $t_0 \le t < \infty$ and on the parameter $\varepsilon$ for $0 \le \varepsilon \le \varepsilon _0$ and $x \in D, D \subset {\mathbb {R}}^n$; the dot represents differentiation with respect to t. The smoothness implies that we can write the right-hand side as $f(t, x, \varepsilon ) = f(t, x, 0) + O(\varepsilon )$.

A well-known example is the pendulum with oscillating support as displayed in Fig. 1.

A much more complicated problem is that of the rotating flywheel on a vibrating foundation displayed in Fig. 2. This problem is discussed in Sect. 8.

There are many more physical examples of such problems, see for instance [18], also [11] and [12].

In modelling the pendulum system of Fig. 1, the Equation of motion for the angle $\theta$ with the vertical yields after linearisation near $\theta =0$:

$$\begin{aligned} \ddot{x} + (\omega ^2 + \varepsilon \cos \nu t)x = 0. \end{aligned}$$

(2)

Studying differential equations, in particular initial value problems, it seems natural to assume the presence of timelike variables $t, \varepsilon t, \varepsilon ^2 t, \ldots$ on which approximate solutions depend. In other mechanical problems, we have similar choices by scaling of spatial variables; as an example, the rotating flywheel problem is displayed in Fig. 2, it is discussed in Sect. 8. Contrasting with the approach of apriori guessing timelike and spatial variables are several other methods like averaging or renormalisation, normal form methods, where no apriori assumptions on the form of time-dependence or hidden spatial scales are made.

The multiple timing idea of assuming the presence of timelike variables was given already by Krylov and Bogoliubov in 1935 [13]; an application can be found in a paper by Kuzmak in 1959 [14]. After that, according to [15], the Kiev school of mathematics had no interest in multiple timing.

Fig. 1

The pendulum has a vertical, harmonically oscillating support P, and it is described in Sect. 5

Fig. 2

A rotating flywheel has a small eccentric mass and is mounted on a spring. It can move through resonance but it can also move into a resonance domain and be locked. The analysis of the model can be found in Sect. 8

Much later multiple timing was studied in the 60 s and 70 s in [4, 9] and for instance [18]. In these papers, there is no reference to [13]. Spatial scaling in problems that did not present itself as singular perturbations with boundary layers came later. Small domains with different qualitative behaviour can be hidden in x-space D of equations like (1).

The scientific literature is rich on papers on the approximation of solutions of ODEs like (1), we can cite only a few of them. A critical comparison of averaging and multiple timing by a number of important examples can be found in [10]; this was the first paper to show weak points of multiple timing. In [30], the relation between averaging, multiple timing and the renormalisation method was discussed following [2, 3] and [16]. In [19], the asymptotic equivalence of the averaging method and multiple timing at first order in $\varepsilon$ was established for standard variational equations like

$$\begin{aligned} {\dot{x}} = \varepsilon f(t, x) \end{aligned}$$

with $O(\varepsilon )$ error estimate on intervals of time of order $1/ \varepsilon$. See also the extensive discussions in [17] and [23].

The following concepts and description are based on [23] ch. 1.

Asymptotic equivalence of methods would imply that, considering a solution of a differential equation x(t), expressions ${\bar{x}}_1(t)$ and ${\bar{x}}_2(t)$ obtained by different methods would both represent an approximation of x(t) with error $\delta (\varepsilon )= o(1)$ as $\varepsilon \rightarrow 0$ on the same interval of time (for instance of size $1/ \varepsilon$). Asymptotic expansions are not unique; ${\bar{x}}_1(t)$ and ${\bar{x}}_2(t)$ may be different but both acceptable approximations.

Following [23], we will indicate that an approximation with error $\delta (\varepsilon )$ is valid on an interval of size $1/ \varepsilon$. A more precise statement is that the error estimate is valid for $t_0 \le \varepsilon t \le t_0 +L$ with $t_0, L$ constants independent of $\varepsilon$.

1.1 Set-up of the paper

To anticipate simple timelike variables as t and $\varepsilon t$ is not a bad idea in the cases that the set of solutions, or if you wish the dynamics of the problem is studied in a structural stable setting. We mean by this that there are no qualitative changes in the behaviour of the solutions; later we will be more precise about structural stability. However, if there is a qualitative change in the dynamics, we may find the presence of unusual or unexpected timelike variables and spatial domains.

A serious point is then that in research, we will be especially interested in structural changes like the emergence of periodic solutions, stability changes, the presence of tipping points in dynamics, etc. Anticipating the timelike variables of a problem like $\varepsilon t, \varepsilon ^2 t$, etc. conflicts with having an open mind about the possible outcome of research.

In Sects. 2 and 3, we will review multiple timing and averaging, and we explain the need and presence of algebraic timelike variables like $\varepsilon ^q t$ with q a rational number in Sect. 4. Such variables arise in stability problems after linearisation at an equilibrium and in standard bifurcations that are found in many applications. In Sects. 4 and 5, we show that structural stability problems of matrices produce already unexpected timelike variables in linear ODEs.

Analysing nonlinear perturbation problems, we have to use bifurcation theory, when discussing for instance the Van der Pol-equation the use of Hopf bifurcation is natural. Bifurcation theory is a large field, we discuss only a few prominent cases.

A different topic starts with Sect. 7. In equations like (1) describing oscillatory behaviour, there may arise local resonance manifolds in x-space that are characterised by small spatial size and unexpected timelike variables. The presence of resonance manifolds is not obvious and requires analysis. These problems are tied in with passage through resonance and capture into resonance. Interestingly, such problems are found in both conservative and dissipative problems. In Sect. 8, we consider dissipative ODEs, in Sect. 9 Hamiltonian systems. A few examples show that we have to develop fairly high order approximations to characterise the dynamics.

A short discussion of other methods and some conclusions are given in Sect. 11.

2 The multiple timescale method

Many small $\varepsilon$ parameter problems are studied using timescales like $t, \varepsilon t$, $\varepsilon ^2t$ and in general $\varepsilon ^n t$ with $n \in \mathbb {N}$. A simple but typical form of multiple timing runs as follows. Consider the equation

$$\begin{aligned} {\dot{x}} = \varepsilon f(t, x) \end{aligned}$$

(3)

with f(t, x) T-periodic in t, the initial value x(0) is given. We will look for solutions of the form

$$\begin{aligned} x(t) = x_0(t, \tau ) + \varepsilon x_1(t, \tau ) + \varepsilon ^2 \ldots \end{aligned}$$

(4)

with $\tau = \varepsilon t$, the dots represent the higher order expansion terms. As the unknown functions $x_0, x_1, \ldots$ are supposed to depend on two variables, we have to transform the differential operator; we have to first order in $\varepsilon$:

$$\begin{aligned} \frac{d}{dt} = \frac{\partial }{\partial t} + \varepsilon \frac{\partial }{\partial \tau }. \end{aligned}$$

Using this differential operator and the expansion, we find

$$\begin{aligned}{} & {} \frac{\partial x_0}{\partial t} + \varepsilon \frac{\partial x_0}{\partial \tau } + \varepsilon \frac{\partial x_1}{\partial t} + \varepsilon ^2 \ldots \\{} & {} \quad = \varepsilon f(t, x_0(t, \tau ) + \varepsilon x_1(t, \tau ) + \varepsilon ^2 \ldots ) \end{aligned}$$

Suppose we can Taylor-expand the function f to a certain order, collecting then the terms of order 1 and $\varepsilon$, we find the simple partial differential equations

$$\begin{aligned} \frac{\partial x_0}{\partial t}= & {} 0, \\ \frac{\partial x_1}{\partial t}= & {} - \frac{\partial x_0}{\partial \tau } + f(t, x_0). \end{aligned}$$

The first equation produces

$$\begin{aligned} x_0(t, \tau ) = A(\tau ), A(0) = x(0), \end{aligned}$$

with $A(\tau )$ still an unknown function; A will be determined in the next step. For $x_1$ we find by integration

$$\begin{aligned} x_1(t, \tau ) = \int _0^t \left( - \frac{\partial A(\tau )}{\partial \tau } + f(s, A(\tau )) \right) ds + B(\tau ). \end{aligned}$$

The function $B(\tau )$ is unknown and has to satisfy $B(0)=0$. If we are looking for bounded solutions of Eq. (3), or even for periodic solutions, the integral

$$\begin{aligned} \int _0^t \left( - \frac{\partial A(\tau )}{\partial \tau } + f(s, A(\tau )) \right) \textrm{d}s \end{aligned}$$

has to be bounded. This is called the secularity condition. We can achieve this by determining $A(\tau )$ such that

$$\begin{aligned} \frac{\textrm{d}A}{\textrm{d} \tau } = \frac{1}{T} \int _0^T f(s, A(\tau )) \textrm{d}s. \end{aligned}$$

(5)

Assuming that f(t, x) has a Fourier expansion, this is a natural condition as it means that the ‘constant’ term of the expansion vanishes. The determination of $A(\tau )$ implies that satisfying the secularity condition corresponds with averaging the function f(t, x). The idea of secularity conditions can be traced to the end of the 18th century, for instance in the writings of Lagrange and Laplace (see [23]).

Example 1

Consider the Van der Pol-equation

$$\begin{aligned} \ddot{x} + x = \varepsilon {\dot{x}}(1 - x^2),~~ x(0)= r, {\dot{x}}(0)=0. \end{aligned}$$

We will look for solutions of the form (4) in t and $\tau = \varepsilon t$; this leads to the well-known first-order result:

$$\begin{aligned} x_0(t, \tau ) = \frac{r e^{\frac{1}{2} \tau }}{(1+ \frac{r^2}{4}(e^{\tau } - 1))^{\frac{1}{2}}} \cos t. \end{aligned}$$

If we have initially $r=2$, the first-order approximation is periodic. It has been shown that this first-order term represents an $O(\varepsilon )$ asymptotic approximation, valid on the timescale $1/ \varepsilon$; see for instance [23] or [27]. Multiple timing and averaging (see next section) produce the same first-order approximations in this problem.

3 The origin of timelike variables t and $\varepsilon t$

Consider Eq. (1) in the expanded form

$$\begin{aligned} {\dot{x}}= f(x, t, \varepsilon )= f_0(x, t)+ \varepsilon f_1(x, t) + O(\varepsilon ^2),\end{aligned}$$

As this is supposed to be a perturbation problem, we should be able to solve the ‘unperturbed’ problem

$$\begin{aligned} {\dot{x}}_0= f_0(x_0, t), \end{aligned}$$

(6)

to obtain the ‘unperturbed’ solution $x_0(t) = \phi (t, C)$ where C is an n-dimensional constant of integration. Apply variation of constants (Lagrange) by putting

$$\begin{aligned} x = \phi (t, y). \end{aligned}$$

For y we obtain the equation:

$$\begin{aligned} {\dot{y}}= \varepsilon g(y, t) + O(\varepsilon ^2), \end{aligned}$$

(7)

a so-called variational or slowly varying system. Note that variation of constants is in general easier to apply if the unperturbed problem (6) is linear. Averaging or using the multiple timescale method produces a transformed (normal form) equation:

$$\begin{aligned} \dot{{\bar{y}}}= \varepsilon {g^0}({\bar{y}}) + O(\varepsilon ^2), \end{aligned}$$

(8)

a slowly varying equation for ${\bar{y}}$. We have transformed $x \rightarrow y \rightarrow {\bar{y}}$ without giving the details of the process and until this point, no approximation has been applied. Omitting the $O(\varepsilon ^2)$ terms to start the approximation process, and dividing the equation for ${\bar{y}}$ by $\varepsilon$, we note that the ‘natural’ first-order timelike variable for ${\bar{y}}$ is $\tau = \varepsilon t$.

Because of the transformation $x \rightarrow y$, t is the zero-order time variable for the original perturbation problem in x and so we have the variables $t, \varepsilon t$.

The only assumptions until now are smoothness of the vector functions on a suitable domain and the possibility of inversion of the variation of constants relations. We conclude that at first order, t and $\varepsilon t$ are natural variables.

3.1 Averaging techniques

To explain the emergence of unexpected timelike variables, it is necessary to discuss briefly second-order averaging and so we have to begin with first order. Suppose that the variational system (7) has a right-hand side that is T-periodic in t. We will consider the averaged vector field

$$\begin{aligned} g^0(y) = \frac{1}{T} \int _0^T g(y, s) \textrm{d}s, \end{aligned}$$

(9)

where we keep y fixed during integration. Omitting the $O(\varepsilon ^2)$ terms in system (8), we have the approximating system

$$\begin{aligned} \dot{{\bar{y}}} = \varepsilon g^0({\bar{y}}). \end{aligned}$$

(10)

We can derive the error estimate that if $y(0)= {\bar{y}}(0)$ we have $|y(t)- {\bar{y}}(t)|= O(\varepsilon )$ on the timescale $1/ \varepsilon$. For a proof see [23] or [26].

To obtain a second-order approximation is much more work, we will present the idea without all the details. Consider eq. (7) in the form:

$$\begin{aligned} {\dot{y}}= \varepsilon g(y, t) + \varepsilon ^2 h(t, y) + O(\varepsilon ^3), \end{aligned}$$

Put $h^0(y)$ for the average of h(t, y) over t, in general we use the superscript 0 for an averaged vector field. We introduce the $n \times n$ Jacobian matrix Dg(y, t) (differentiation with respect to y only) and the vector field

$$\begin{aligned} u^1(t, y) = \int _0^t (g(s, y) - g^0(y))\textrm{d}s. \end{aligned}$$

We compute the vector field

$$\begin{aligned} F^1(t, y) = Dg(y,t) u^1(t, y), \end{aligned}$$

with average $F^{10}$. Consider the equation:

$$\begin{aligned} {\dot{w}} = \varepsilon g^0(w) + \varepsilon ^2 F^{10}(w) + \varepsilon ^2 h^0(w), w(0) = y(0),\quad \end{aligned}$$

(11)

then the expression $w(t) + \varepsilon u^1(t, w)$ approximates y(t) with error $O(\varepsilon ^2)$ on the timescale $1/ \varepsilon$. For a proof and discussions see [23].

We gave explicitly these expressions to show that we made no assumptions on relevant timelike variables. An $O(\varepsilon )$ approximation produces timelike variable $\varepsilon t$; a subsequent timelike variable will be introduced by solving the variational Eq. (11). We will see examples later.

4 Algebraic timescales for bifurcations

One of the basic questions, often unsolved, of mathematical physics is to obtain a global picture of the behaviour of the dynamical system studied. If the system at hand experiences qualitative changes when the parameters of the system pass certain critical values, we call them bifurcations. This can involve many causes; it can be stability changes, emergence or destruction of solutions, transitions to tori, chaos in its different forms and other phenomena.

As in many research problems the unperturbed problem (6) is linear, we need basic results from matrix theory. In addition, when we will study a special solution like an equilibrium of Eqs. (10) or (11), we will usually linearise near this solution, for instance to determine stability. This also asks for matrix theory.

A second cause of qualitative changes is the bifurcations of a nonlinear part of the vector field when a parameter varies. Standard cases are co-dimension 1 bifurcations like for instance pitchfork and saddle-node; see Sect. 6.

A different cause of qualitative changes will be if in phase-space we find local behaviour as encountered in boundary layers that is very different from the global behaviour. The occurrence of such local changes can be quite unexpected, see Sect. 7.

Fig. 3

The gray Floquet tongues denote for which parameter values $\omega$ and $\varepsilon$ the trivial solution of the Mathieu equation is unstable. In our approximations, we have described the lower part ($\varepsilon$ small) of the tongue emerging from $\omega =1$ as in Eq. (2), the tongue shapes for large values of $\varepsilon$ and other values of $\omega$ were obtained numerically

All this knowledge will help to avoid making incorrect apriori assumptions on timelike and spatial variables.

5 Structural stability of matrices

Part of the (classical) material in this section can be found in [27], in particular appendix 15.3. Before formulating the theory, we consider as an introduction the Mathieu equation (2) in its fundamental 1 : 2-resonance with a slight detuning of the frequency $\omega$. The equation models the pendulum motion with oscillating support shown in Fig. 1. Near the vertical axis linearisation and replacing $\theta$ by x leads to the equation:

$$\begin{aligned} \ddot{x} + (1 + \varepsilon a + \varepsilon ^2 b + \varepsilon \cos 2t)x = 0, \end{aligned}$$

(12)

with $\omega ^2 = 1 + \varepsilon a + \varepsilon ^2 b$; a and b are free parameters independent of $\varepsilon$. See also Fig. 1.

We summarise the second-order approximation analysis in [27]. We apply Lagrange variation of constants $x, {\dot{x}} \mapsto y_1, y_2$ to Eq. (12):

$$\begin{aligned} x=y_1 \cos t + y_2 \sin t,\,\, {\dot{x}}= -y_1 \sin t + y_2 \cos t. \end{aligned}$$

The slowly varying equations for $y=(y_1, y_2)$ are after averaging of the form ${\dot{y}}= A(\varepsilon ) y$;

$$\begin{aligned} A(\varepsilon ) = \varepsilon \left( \begin{array}{cc} 0 &{} \frac{1}{2} (a - \frac{1}{2}) \\ - \frac{1}{2}(a + \frac{1}{2}) &{} 0 \end{array} \right) + O(\varepsilon ^2). \end{aligned}$$

The trivial solution is stable if $|a| > 1/2$, unstable if $|a| < 1/2$. For $a = \pm 1/2$, we have a first-order approximation of the curves separating stability and instability domains, see Fig. 3. The matrix $A(\varepsilon )$ is singular if $a = \pm 1/2$. The Floquet tongues are bounded by the bifurcation curves where the transition from unstable to stable solutions takes place in ($\omega ^2, \varepsilon$)-parameter space.

What happens at the tongue boundary, for instance if $\omega ^2= 1 + \varepsilon a$ with $a= 1/2\,$? In this case we have to first order:

$$\begin{aligned} A_1 = \left( \begin{array}{cc} 0 &{} 0 \\ - \frac{1}{2} &{} 0 \end{array} \right) , \end{aligned}$$

a typical degenerate matrix from bifurcation theory. Following [23] or [27] we perform second-order averaging following Sect. 3.1 to find as perturbation of $A_1$:

$$\begin{aligned} A_2 = \left( \begin{array}{cc} 0 &{} \frac{1}{64} + \frac{1}{2} b \\ \frac{7}{64} - \frac{1}{2} b &{} 0 \end{array} \right) ,\,\, {\dot{y}}= \varepsilon A_1 y + \varepsilon ^2 A_2 y \end{aligned}$$

We find for the eigenvalues of $A(\varepsilon )$ to this second order of approximation

$$\begin{aligned} \lambda ^2 = - \frac{1}{4} \left( b + \frac{1}{32}\right) \varepsilon ^3 + \frac{1}{4} \left( b + \frac{1}{32}\right) \left( \frac{7}{32} - b\right) \varepsilon ^4. \end{aligned}$$

The $O(\varepsilon ^3)$-term dominates, $b = - \frac{1}{32}$ produces a more precise location of the Floquet tongue.

Fig. 4

The disc rotates with constant frequency $\Omega$, its foundation produces at point P small vibrations of the form $\varepsilon \cos \omega _0t$

Fig. 5

In the decoupled systems ($\alpha =0$), we have the standard instability tongues where damping decreases the instability domain, see left figure. In the coupled rotating system ($\alpha >0$), the damping $\kappa$ increases the instability, see right figure

Near the boundary of the Floquet tongue we have that $\lambda ^2 = O(\varepsilon ^3)$; ii is remarkable that the timescale $\varepsilon ^{\frac{3}{2}} t$ plays a part in this problem. The timescales characterising the flow near the Floquet tongue are derived from second order of the eigenvalues:

$$\begin{aligned} t,\,\,\varepsilon t,\,\,\varepsilon ^{\frac{3}{2}} t,\,\,\varepsilon ^2 t. \end{aligned}$$

The presence of the timelike variable $\varepsilon ^{\frac{3}{2}} t$ was noted for the Mathieu equation earlier in [2], using the renormalisation method.

5.1 The rotating disc

A heavy disc is rotating on a vertical shaft. The shaft is fixed at its suspension point P, but the centre of the disc is free to make small vibrations in the horizontal directions, see Fig. 4. The point of suspension is elastically attached to the foundation z = 0. As a first approximation, we assume that the suspension point oscillates harmonically in the vertical direction. Following [20], the equations of motion are as follows:

$$\begin{aligned} {\left\{ \begin{array}{ll} \ddot{x}+ 2 \alpha {\dot{y}} + (1+4 \varepsilon \eta ^2 \cos 2 \eta t)x + \varepsilon \kappa {\dot{x}} &{} =0,\\ \ddot{y} -2 \alpha {\dot{x}} + (1+4 \varepsilon \eta ^2 \cos 2 \eta t)y + \varepsilon \kappa {\dot{y}} &{} =0, \end{array}\right. } \end{aligned}$$

(13)

with $\alpha$ dependent on the inertial moments and inverse proportional to the rotational speed $\Omega$, for the vibration of the foundation we have a harmonic function. Damping is added with positive coefficient $\kappa$.

In [20], the case $\kappa =0$, no damping, is analysed first. The frequencies in the case $\varepsilon = 0$ are as follows:

$$\begin{aligned} \omega _1 = \sqrt{1+ \alpha ^2} + \alpha , \, \omega _2 = \sqrt{1+ \alpha ^2} - \alpha . \end{aligned}$$

(14)

We have a so-called sum resonance if $\omega _1+ \omega _2= 2 \sqrt{1+ \alpha ^2} =2 \eta$. Introducing detuning as in Eq. (12), we obtain the same timelike variables characterising the dynamics. For stability boundaries for the position on the vertical axis, we find to first order in $\varepsilon$:

$$\begin{aligned} \eta = \sqrt{1+ \alpha ^2} (1 \pm \varepsilon ). \end{aligned}$$

(15)

For the standard calculations on Mathieu equations see also [26]. Mechanical rotation effects in combination with the parametric resonance produces with $\kappa =0$ an instability tongue depicted in Fig. 5. A remarkable result is found if we add small damping; if $\kappa >0$, we find by eigenvalue analysis of the matrices the stability boundaries to order $\varepsilon$:

$$\begin{aligned} \eta = \sqrt{1+ \alpha ^2} (1 \pm \varepsilon \sqrt{1+ \alpha ^2}). \end{aligned}$$

(16)

As this result is valid for arbitrary positive $\kappa$, the resulting boundaries differ essentially from the stability boundaries given by (15). The domain of instability becomes actually larger when damping is introduced. Mathematically, this phenomenon is caused by the structural instability of matrices as explained in [8]. Physically, it can be understood from the fact that damping introduces an extra coupling between the 2 degrees of freedom of the rotating disc. See also Fig. 5.

Instability caused by damping is an important phenomenon in 2 or more degrees-of-freedom systems with rotating components. For introductory surveys see [11] and [12].

5.2 Remark on weak coupling and damping

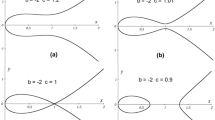
It is interesting to consider the case of a weaker coupling of the rotating system by putting $\alpha \mapsto \varepsilon \alpha$. One can also put $\kappa \mapsto \varepsilon \kappa$. With these assumptions, the stability matrix requires a second-order averaging calculation, and the resulting $4 \times 4$ matrix contains elements with terms mixed of $\varepsilon$ and $\varepsilon ^2$. To first order, we have the situation of Fig. 5 (left figure) without damping. It is not known if adding the terms $O(\varepsilon ^2)$ may produce qualitative and quantitative changes.

5.3 Results on stability of matrices

We start with Eq. (1) of the form ${\dot{x}}= f(x, t, \varepsilon )$ to find an equilibrium or special solution $\psi (t)$ and study the behaviour of this solution as the parameters are changing; we need to calculate eigenvalues, Lyapunov exponents or characteristic multipliers. As we saw in the Mathieu equation and will also see in the examples later on, bifurcation phenomena in ODEs lead by averaging and local linearisation to studying systems of the form:

$$\begin{aligned} {\dot{x}}= A(\varepsilon ) x. \end{aligned}$$

We assume that we can expand

$$\begin{aligned} A(\varepsilon )=A_0 + \varepsilon A_1 + \varepsilon ^2 A_2 + \varepsilon ^3 \ldots \end{aligned}$$

The $n \times n$-matrices $A_n$ are independent of $\varepsilon$. Usually, we have $A_0$ derived from the unperturbed problem, $A_1$ is produced by perturbation methods, and sometimes we will have some knowledge about higher order terms. An important question is then if the eigenvalues of $A_0$ and $A_0+ \varepsilon A_1$ are in a sense typical for the eigenvalues of $A(\varepsilon )$. This question is determined by the structural stability of the matrices and whether eigenvalues are single or multiple. Failure of structural stability and the presence of multiple eigenvalues is characteristic for bifurcation phenomena.

We give a definition:

A $n \times n$ matrix is called structurally stable if it is nonsingular and all eigenvalues have nonzero real part. If we have a zero eigenvalue or purely imaginary eigenvalues, we can expect bifurcations. As we shall see later on, multiple eigenvalues may affect the form of the expansions and timelike variables.

Multiple eigenvalues of the matrix $A_0$ or $A_0 + \varepsilon A_1$ may produce eigenvalues of the order $\varepsilon ^q$ with q a rational number. Consequently timelike variables like $\varepsilon ^{q}t$ play a part. We can predict the occurrence of such algebraic timescales from the actual eigenvalues. We add an example.

Example 2

Consider a system that can be obtained from linearisation near an equilibrium of a chemical reaction equation or an interacting system in population dynamics:

$$\begin{aligned} {\dot{x}}_1= & {} - \varepsilon x_1 + \varepsilon x_2 + \varepsilon ^2 x_3, \end{aligned}$$

(17)

$$\begin{aligned} {\dot{x}}_2= & {} \varepsilon ax_2 - \varepsilon a x_3, \end{aligned}$$

(18)

$$\begin{aligned} {\dot{x}}_3= & {} (\varepsilon a -\varepsilon ^2b) x_2 -\varepsilon ax_3, \end{aligned}$$

(19)

with constants $a,b >0$. The eigenvalues of the coefficient matrix are as follows:

$$\begin{aligned} - \varepsilon , \pm \varepsilon ^{3/2} \sqrt{ab} \end{aligned}$$

with timelike variables $\varepsilon t, \varepsilon ^{3/2} t.$

5.4 Classical results

Results for timelike variables from matrix expansions are essential for a sound analysis of our problems. We summarise a few 19th century results referring to [27] appendix 15.3 for references. Consider the matrix expansion with $A_0$ structurally stable:

$$\begin{aligned} A(\varepsilon )=A_0 + \varepsilon A_1 + \varepsilon ^2 A_2 + \varepsilon ^3 \ldots \end{aligned}$$

• 1. If $\lambda _0$ is single, we have

  $$\begin{aligned} \lambda (\varepsilon ) = \lambda _0 + \varepsilon \lambda _1 + \varepsilon ^2 \ldots \end{aligned}$$

• 2. According to Newton-Puisieux: If $\lambda _0$ is multiple, fractional powers of $\varepsilon$ are possible in the expansion of the eigenvalues.

Example 3

Newton-Puisieux expansion

Consider again the equation ${\dot{x}} = A(\varepsilon ) x$ with for the matrix $A(\varepsilon )$:

$$\begin{aligned} A(\varepsilon ) = \varepsilon \left( \begin{array}{cccc} 1 &{} 0 &{} 0 &{} 0 \\ 1 &{} 1 &{} 0 &{} 0 \\ 0 &{} -1 &{} 1 &{} 0 \\ 0&{} 0&{} 0&{} 1 \end{array} \right) + \varepsilon ^2 \left( \begin{array}{cccc} 0 &{} 0 &{} 1 &{} 0\\ 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 1 &{} 0 \end{array} \right) \end{aligned}$$

$A_0$ is the matrix with zero elements so we consider $A_1$. The characteristic equation of $\varepsilon A_1$ produces 4 equal eigenvalues $\varepsilon$. The matrix $\varepsilon A_1 + \varepsilon ^2 A_2$ has the characteristic equation:

$$\begin{aligned} (\varepsilon - \lambda ))((\varepsilon - \lambda )^3 - \varepsilon ^4) = 0. \end{aligned}$$

The eigenvalues are as follows:

$$\begin{aligned} \lambda _{1} {=} \varepsilon , \lambda _2 {=} \varepsilon - \varepsilon ^{4/3}, \lambda _{3, 4}= \varepsilon - \frac{1}{2}(-1 \pm i \sqrt{3})\varepsilon ^{4/3}. \end{aligned}$$

Again we find timelike variables with a fractional exponent of $\varepsilon$.

6 Co-dimension 1 bifurcations

The theory of bifurcations is a large and well-researched topic. Bifurcations, qualitative changes in the dynamics, are often found when analysing variational equations. This leads often to interesting phenomena in a nonlinear setting where certain parameter values are identified that may cause qualitative changes We consider here the simplest but often occurring case where we have one or two parameters involved. The examples we discuss are low dimensional, so-called co-dimension 1 bifurcations. Such bifurcations may arise in subsystems of ODEs after first- or second-order averaging.

A simple example is the saddle-node bifurcation described by:

$$\begin{aligned} {\dot{x}} = a - bx^2. \end{aligned}$$

(20)

If $ab <0$, there is no critical point; suppose $ab >0$, then we have the critical points $x_0 = \pm \sqrt{a/b}$. Their stability and local behaviour with time is described by the coefficient of linearisation $-2bx_0 = \mp 2 \sqrt{ab}$ near the critical points. If for instance $a= \varepsilon ^2, b = \varepsilon$, the leading timelike variable is $\varepsilon ^{3/2} t$.

Consider the system inspired by the pitchfork bifurcation:

$$\begin{aligned} {\dot{x}} = \varepsilon ^2 y - \varepsilon y^3,\, {\dot{y}} = \varepsilon x. \end{aligned}$$

(21)

Three critical points (equilibria) are $(x_0, y_0)= (0, 0), (0, \pm \sqrt{\varepsilon })$. Linearisation near the critical points $(o, y_0))$ produces:

$$\begin{aligned} {\dot{x}} = \varepsilon ^2 y - 3 \varepsilon y_0^2 y+ \ldots ,\, {\dot{y}} = \varepsilon x, \end{aligned}$$

where the dots represent the neglected nonlinear terms. We have the characteristic eigenvalue equations and timelike variables near the critical points:

(0, 0): $\lambda ^2 - \varepsilon ^3=0$, timelike variable $\varepsilon ^{3/2} t$.

$(0, \pm \sqrt{\varepsilon })$: $\lambda ^2 -2 \varepsilon ^3=0$, timelike variable $\varepsilon ^{3/2} t$.

In general, we expect in regions where bifurcations occur and for higher dimensional problems the presence of timelike variables of the form $\varepsilon ^q t$ with q a positive rational number.

As we will see, an example of the pitchfork bifurcation is found for the amplitude in the Van der Pol-equation.

Example 4

Consider the Van der Pol-equation in the following form:

$$\begin{aligned} \ddot{x} + x = \varepsilon {\dot{x}} (a -x^2). \end{aligned}$$

(22)

If parameter $a <0$, the oscillations will be damped, and there is no periodic solution. With $a>0$, we have after first-order averaging

$$\begin{aligned} {\dot{r}} = \frac{\varepsilon }{2} r (a- \frac{1}{4}r^2),\, {\dot{\phi }} =0. \end{aligned}$$

(23)

If parameter a starts at a negative value and we let it increase, it will pass through zero and for $a>0\,$ a periodic solution emerges with amplitude $2 \sqrt{a}$ by a pitchfork bifurcation. It starts with a being small, say $a= \varepsilon$. This is the situation where we have the timelike variable $\varepsilon ^{3/2} t$. We improve the reasoning by writing Eq. (22) as:

$$\begin{aligned} \ddot{x} + x = -\varepsilon {\dot{x}} x^2 + \varepsilon ^2 {\dot{x}}. \end{aligned}$$

In amplitude-phase variables $r, \phi$ the variational system to $O(\varepsilon )$ becomes:

$$\begin{aligned} {\dot{r}}= & {} - \varepsilon r^3 \sin ^2(t+ \phi ) \cos ^2(t+ \phi ),\\ {\dot{\phi }}= & {} - \varepsilon r^2 \sin (t+ \phi ) \cos ^2(t+ \phi ). \end{aligned}$$

First-order averaging produces:

$$\begin{aligned} {\dot{r}}= - \varepsilon \frac{1}{8}r^3,\, {\dot{\phi }}=0. \end{aligned}$$

Computing the quantities Df and $u^1$ in the notation of Sect. 3.1, we find an $O(\varepsilon ^2)$ contribution for the phase and the amplitude; for the amplitude we have:

$$\begin{aligned} {\dot{r}} = - \varepsilon \frac{1}{8}r^3 + \varepsilon ^2 \frac{r}{2}. \end{aligned}$$

(24)

We find that the the amplitude of the periodic solution grows as $2 \sqrt{ \varepsilon }$.

7 Resonance manifolds

To obtain variational equations can be more difficult if the unperturbed system $\varepsilon = 0$ of Eq. (1) is nonlinear. In such cases, we may obtain a formulation like:

$$\begin{aligned} {\left\{ \begin{array}{ll} {\dot{x}} = \varepsilon X(x, \phi ) + O(\varepsilon ^2),\\ {\dot{\phi }} = \Omega (x) + O(\varepsilon ), \end{array}\right. } \end{aligned}$$

(25)

with x a Euclidean n-vector, $\phi = (\phi _1, \ldots , \phi _m)$ a m-dimensional angle-vector. The order functions multiplying the right-hand sides are different, the variations of the angle $\phi$ are O(1) unless we are in a neighbourhood of the zeros of the vector field $\Omega (x)$.

In general, the Fourier expansion of $X(x, \phi )$ will contain combinations of the angles $(\phi _1, \ldots , \phi _m)$. As we will see, in systems of the form (25) we have to account for the presence of resonance manifolds.

Problems of this type arise both in dissipative and in Hamiltonian systems; see for instance [23] or [27] and references there. Also, in these problems, higher order algebraic timescales and asymptotically small domains are natural. We start with a simple example.

Example 5

Consider the system:

$$\begin{aligned} {\left\{ \begin{array}{ll} {\dot{x}} = \varepsilon (1+x \cos \phi _1 +(1-x)\\ \cos (2 \phi _1- \phi _2)), x(0)=1,\\ {\dot{\phi }}_1 = 2,\\ {\dot{\phi }}_2 = x^2, \end{array}\right. } \end{aligned}$$

(26)

Fig. 6

Solution of system (26) starting at $x(0)=1, \phi _1(0)=0, \chi (0)=1.929$; $\varepsilon =0.1$. The solution remains for some time oscillating in the resonance domain near $x=2$

Fig. 7

Solutions x(t) of system (31) starting for $\chi (0)=0$ (left, stable) and for $\chi (0)= - \pi$ (right, unstable) starting near equilibrium; $x(0)=1, \varepsilon = 0.05$. The initial conditions have error $\sqrt{\varepsilon }$

The vector field $X(x, \phi )$ is scalar in this case and contains 2 angles, $\phi _1$ and the combination angle $2 \phi _1- \phi _2$. Putting $\chi = 2 \phi _1- \phi _2$ for the combination angle we have:

$$\begin{aligned} {\dot{\chi }} = 4-x^2. \end{aligned}$$

(27)

As $\phi _1(t) = 2t+ \phi _1(0)$, this angle is timelike. The angle $\chi$ is timelike except in a neighbourhood of $x = \pm 2$. Averaging over the angles $\phi _1$ and $\chi$ outside a neighbourhood of $x = \pm 2$, we find:

$$\begin{aligned} x(t) = 1+ \varepsilon t + \varepsilon ^2 \ldots \end{aligned}$$

A neighbourhood of $x = \pm 2$ will be called a resonance domain, $x=2$ a resonance manifold. Note that the approximate solution starts in $x=1$ and will increase to $x=2$, so it enters the resonance domain near $x=2$. To determine the size of the resonance domain and the local dynamics, we rescale:

$$\begin{aligned} x= 2+ \delta (\varepsilon ) \xi , \end{aligned}$$

(28)

with $\delta (\varepsilon ) \rightarrow 0$ as $\varepsilon \rightarrow 0$ ($\delta$ is a small parameter to be determined). From system (26) we find:

$$\begin{aligned} {\left\{ \begin{array}{ll} \delta \xi = \varepsilon (1+ \cos \phi _1 - \cos \chi ) + O(\varepsilon \delta ), \\ {\dot{\chi }} = -4 \delta \xi +O( \delta ^2). \end{array}\right. } \end{aligned}$$

(29)

The 2 equations are balanced if $\delta (\varepsilon ) = \sqrt{\varepsilon }$; in the theory of singular perturbations, this is called a significant degeneration of the system, see for the theory [27]. With this assumption, the small size of the resonance domain near $x=2$ is $\sqrt{\varepsilon }$. After omitting the higher order terms and averaging over $\phi _1$, we have

$$\begin{aligned} {\dot{\xi }} = \sqrt{\varepsilon } (1 - \cos \chi ), {\dot{\chi }} = -4 \sqrt{\varepsilon } \xi , \end{aligned}$$

so that by differentiation we find the forced pendulum equation for $\chi$ in the resonance domain:

$$\begin{aligned} \ddot{\chi } + 4 \varepsilon \cos \chi = 4 \varepsilon . \end{aligned}$$

To first order the timescale of the dynamics in the resonance domain and manifold is $O( \sqrt{\varepsilon })$, the timelike variable $\sqrt{\varepsilon } t$, the error of the first approximation will also be $O( \sqrt{\varepsilon })$, see Fig. 6. Note that this resonance domain is in a sense hidden in system (26).

We will see that the size of resonance manifolds and the timescale found in this simple problem are typical for much more complicated problems. Even for dissipative systems of the form (25), the first-order approximation of the solutions in a resonance domain will always be conservative; dissipation may be shifted to second order (Fig. 7).

8 Resonance manifolds in dissipative systems

A typical example from [27], example 12.11, describes a slightly eccentric flywheel, see Fig. 2. in the Introduction. The vertical displacement x of the flywheel and its rotation angle $\phi$ are given by

$$\begin{aligned} \ddot{x} + x= & {} \varepsilon (-x^3 - {\dot{x}} + {\dot{\phi }}^2 \cos \phi ) + O(\varepsilon ^2), \\ \ddot{\phi }= & {} \varepsilon (\frac{1}{4}(2 - {\dot{\phi }}) + (1-x) \sin \phi ) + O(\varepsilon ^2). \end{aligned}$$

It turns out that there exists a resonance domain; the domain is of size $O(\varepsilon ^{\frac{1}{2}})$, the timelike variable of the dynamics is $\sqrt{\varepsilon } t$ in the resonance domain. A difference with conservative systems is the possibility of locking into resonance for various initial conditions in this mechanical problem where we have both flywheel and spring oscillating. For details, we refer to [27] and the references there.

Example 6

A simpler example is the 3-dimensional system:

$$\begin{aligned} {\left\{ \begin{array}{ll} {\dot{x}} = \varepsilon f(x)( \cos \phi _1 + \cos (2 \phi _1- \phi _2)), x(0)=1,\\ {\dot{\phi }}_1 = x^2+1, \\ {\dot{\phi }}_2 = -1. \end{array}\right. } \end{aligned}$$

(30)

The function f(x) is smooth. The equation for x contains 2 angles, $\phi _1$ and $\chi = 2 \phi _1- \phi _2$. The angle $\phi _1$ is clearly timelike for any value of x; we can average over $\phi _1$. We have for $\chi$:

$$\begin{aligned} {\dot{\chi }} = 2x^2+3, \end{aligned}$$

so $\chi$ is also timelike. Averaging over both angles we find ${\dot{x}} =0$ and the trivial dynamics $x(t) = x(0) + O(\varepsilon )$. One can check this result numerically for instance for the choices $f(x)=x$ and $f(x)=\sin x$. For $\varepsilon = 0.1$, the error stays below 0.1.

A less trivial dynamics is shown in the following example.

Example 7

   

$$\begin{aligned} {\left\{ \begin{array}{ll} {\dot{x}} = \varepsilon f(x)( \cos \phi _1 - \cos 2 \phi _2 - \sin (2 \phi _1- \phi _2)), \\ {\dot{\phi }}_1 = x^2+0.5, \\ {\dot{\phi }}_2 = 3. \end{array}\right. } \end{aligned}$$

(31)

The function f(x) is smooth, $f(1)=1$. Again the angle $\phi _1$ is clearly timelike and so is $\phi _2$, we can average over $\phi _1, \phi _2$ to find the approximate equation

$$\begin{aligned} {\dot{x}} = - \varepsilon f(x) \sin (2 \phi _1- \phi _2), \end{aligned}$$

producing $O(\varepsilon )$ approximations outside resonance domains.

Fig. 8

Solutions x(t) of system (31) starting for $\chi (0)=- \pi , x(0)=1$ near equilibrium but for $\varepsilon = 0.005$ with error $\sqrt{\varepsilon }$

We have for $\chi$:

$$\begin{aligned} {\dot{\chi }} = 2(x^2-1), \end{aligned}$$

with resonance domains in a neighbourhood of $x= \pm 1$. Near $x=1$ we scale

$$\begin{aligned} x= 1+ \delta (\varepsilon ) \xi \end{aligned}$$

to find to first order the system:

$$\begin{aligned} \delta {\dot{\xi }} = - \varepsilon f(1) \sin \chi ,\, {\dot{\chi }}= 4 \delta \xi . \end{aligned}$$

To balance the equations, we choose $\delta (\varepsilon )= \sqrt{\varepsilon }$ leading to the first-order equation for $\chi$:

$$\begin{aligned} \ddot{\chi }+ 4 \varepsilon \sin \chi = 0. \end{aligned}$$

(32)

The timelike variable in the resonance domain is again $\sqrt{\varepsilon } t$, and the approximations at this order have error $O(\sqrt{\varepsilon } )$. Critical points (equilibria) of the pendulum equation Eq. (32) are found for solutions of $\sin \chi = 0$.

If $\chi =0$, the solutions are to first order neutrally (Lyapunov) stable; for $\chi = \pi$, we have instability. As the second equilibrium is a saddle point, the instability persists to all orders of $\varepsilon$. It is interesting the repeat the computation for $\varepsilon = 0.01$, see Fig. 8.

9 Hamiltonian resonance

The following results are based on [21, 23] and [27]. Consider the two degrees-of-freedom (dof) Hamiltonian in local coordinates with Taylor-expansion:

$$\begin{aligned} {H} = {H}{}_{2} + \varepsilon {H}{}_{3} + \varepsilon ^2 {H}{}_{4} +O(\varepsilon ^3), \end{aligned}$$

(33)

with ${H}{}_{k}$ homogeneous polynomials of degree k ($=2, 3, \ldots$) in positions and momenta (p, q). ${H}{}_{2}$ takes the standard form

$$\begin{aligned} H_2 = \frac{m}{2} ( q_1^2 + p_1^2 ) + \frac{n}{2} ( q_2^2 + p_2^2 ), \end{aligned}$$

(34)

with the integers m, n positive and in most cases relative prime. The phase-flow in a neighbourhood of the origin takes place on compact manifolds parametrised by the Hamiltonian (energy) integral. Resonance domains can be found but because of the recurrence properties of the phase-flow capture into resonance is not possible. Near the origin of phase-space Hamiltonian (33) was obtained by rescaling $q= \varepsilon {\bar{q}}, p= \varepsilon {\bar{p}}$, dividing by $\varepsilon ^2$ in the Hamiltonian and leaving out the bars.

Most of the attention in the literature went to the primary resonance 1 : 2 and to the secondary resonances 1 : 1 and 1 : 3, see [23]. In these resonance cases, the dominant part of the phase-flow is characterised by the timescales $t, \varepsilon t, \varepsilon ^2t$ and the time intervals of validity of approximation $1/ \varepsilon$ and $1/ \varepsilon ^2$. This picture changes drastically for higher order resonance.

9.1 The higher order normal form

The frequency cases where $m+n \ge 5$ are called higher order resonances by definition. To study these resonances, we have to compute higher order normal forms; this involves intervals of time longer than $1 / \varepsilon$, even longer than $1/ \varepsilon ^2$. In the Hamiltonian normal form, the first resonant term, involving not only actions but also angles, arrives from $H_{m+n}$ at $O({\varepsilon }^{ m + n - 2 })$.

The first basic approach to higher order resonance was given in [21] with applications in [22]. In [25], an improvement of the estimates has been given, together with a number of applications, for instance the elastic pendulum. Introducing action-angle variables $p_i, q_i \rightarrow \tau _i, \phi _i, \,i=1, 2$, with $\tau _i = \frac{1}{2}(q_i^2+p_i^2), i= 1, 2$ and

$$\begin{aligned} p_i= \sqrt{2 \tau _i} \cos \phi _i,\, q_i= \sqrt{2 \tau _i} \sin \phi _i,\, i=1,2, \end{aligned}$$

the normal (averaged) form is obtained by near-identical transformation and will look like

$$\begin{aligned} H= & {} m \tau _1 + n \tau _2 + \varepsilon ^2 {\bar{H}}_4(\tau _1, \tau _2) \nonumber \\{} & {} + \ldots + \varepsilon ^{m+n-2}D(\tau _1^n \tau _2^m)^{\frac{1}{2}} \cos \chi , \end{aligned}$$

(35)

with resonance combination angle

$$\begin{aligned} \chi = n \phi _1 - m \phi _2 + \alpha . \end{aligned}$$

(36)

${\bar{H}}_4$ is the normal form of the terms $\varepsilon {H}{}_{3} + \varepsilon ^2 {H}{}_{4}$. The dots represent terms depending on $\tau _1, \tau _2$ only. These are the terms in so-called Birkhoff normal form. A consequence from the corresponding equations of motion is that the actions are constant until and not included terms of order $O(\varepsilon ^{m+n-2})$. The normal form for the Hamiltonian including terms $O(\varepsilon ^{m+n-3})$ is integrable with integrals

$$\begin{aligned} m \tau _1 + n \tau _2= E_0,\, \tau _1= E_1, \end{aligned}$$

with $E_0, E_1$ constants. for the combination angle we have

$$\begin{aligned} {\dot{\chi }}= \varepsilon ^2 \left( n \frac{\partial {\bar{H}}_4}{\partial \tau _1} - m \frac{\partial {\bar{H}}_4}{\partial \tau _2}\right) + \varepsilon ^3 \ldots \end{aligned}$$

(37)

To compute the term ${\bar{H}}_4$, we can use second-order averaging. The Hamiltonian and equations of motion truncated after $\varepsilon ^2$-terms produce an $O(\varepsilon )$ approximation of the solutions on the timescale $1/ \varepsilon ^2$.

To determine the term to order $O(\varepsilon ^{m+n-2})$ is in general a lot of work.

9.2 The phase-flow of higher order resonance for 2 dof

We summarise. Consider for 2 dof time-independent Hamiltonians near stable equilibrium the higher order resonances as defined by $m+n \ge 5$. When averaging we usually transform to amplitude-phase variables before averaging over t. We can use instead of the phases $\psi _1, \psi _2$ the timelike variables $\phi _1= mt + \psi _1, \phi _2= nt + \psi _2$. A resonance domain with resonance manifold M exists if we have solutions of:

$$\begin{aligned} n \frac{\partial {\bar{H}}_4}{\partial \tau _1} - m \frac{\partial {\bar{H}}_4}{\partial \tau _2} =0. \end{aligned}$$

(38)

It turns out there are two domains in phase-space where the dynamics is very different and is characterised by different timescales. We have the results:

Proposition 1

   

• The resonance domain $D_I$, which is a neighbourhood of the resonance manifold M. The resonance manifold, if it exists, arises if condition (38) is satisfied. In $D_I$, the variations of the actions (or amplitudes) and the combination angle $\chi = n \phi _1 - m \phi _2 + \alpha$ are found and are of the same nature as in dissipative systems. In terms of singular perturbations, resonance domain $D_1$ is an inner boundary layer of the Hamiltonian system. In [25], it has been shown that the size of the resonance domain is $O(\varepsilon ^{\frac{m+n-4}{2}})$, the interaction of the actions takes place on a time interval of order $O(\varepsilon ^{-\frac{m+n}{2}})$

• The remaining part of phase-space, outside the resonance domain, is $D_0$, the outer domain. In the domain $D_0$, there is, to a high approximation, no variation of the actions, and so hardly any exchange of energy between the two degrees of freedom.

It is shown in [25] that for Hamiltonians derived from a potential, we have $\alpha =0$, and so the combination angle $\chi = n \phi _1- m \phi _2$. For the elastic pendulum, after the first-order 4 : 2-resonance, the higher order 4 : 1-resonance is the most prominent one with resonance manifold of size $O(\varepsilon ^{\frac{1}{2}})$ and time interval of interaction $O(\varepsilon ^{- \frac{5}{2}})$; for a Poincaré map of the 1 : 6-resonance of the elastic pendulum see Fig. 9. It was constructed by numerical integration for fixed energy, the 2 positions $q_1, q_2$ are on the axes with the map arising from the transversal points when passing recurrently the plane $p_2=0$.

Fig. 9

The Poincaré map for the 1 : 6-resonance of the elastic pendulum ($\varepsilon = 0.75$, large for illustration purposes). In the resonance domain, the saddles are connected by heteroclinic cycles and inside the cycles are 6 centre fixed points, see [25]. Figure courtesy SIAM J.Appl.Math

10 A m : n toy problem

A well-known model for orbits in axi-symmetric galaxies is the family of Hénon-Heiles potential problems, see [7]. The applicability of this potential is much more general as symmetry of the potential, think of pendulum equations, occurs in many mechanical problems. A simplification was studied numerically in [5]. Using the notation of [5], the Hamiltonian is as follows:

$$\begin{aligned} H = \frac{1}{2} ( {\dot{x}}^2 + m^2x^2 ) + \frac{1}{2} ( {\dot{y}}^2 + n^2 y^2) - \varepsilon xy^2. \end{aligned}$$

(39)

Fig. 10

Solutions of system (40) using for initial values (43). Projections on physical x, y-space of periodic solutions in the resonance domains are algebraic curves. Shown are the projections of the $m:n= 4:1, 5:2$ and 7 : 3 resonances; $\chi (0)=0$

The equations of motion are as follows:

$$\begin{aligned} \ddot{x} + m^2 x = \varepsilon y^2,\, \ddot{y}+ n^2 y= 2 \varepsilon xy. \end{aligned}$$

(40)

So, the x-normal mode $y={\dot{y}}=0$ is an exact harmonic solution. Using amplitude-phase variables $x= r_1 \cos (mt+\phi _1), {\dot{x}}= -mr_1 \sin (mt+ \phi _1), y= r_2\cos (nt+ \phi _2), {\dot{y}}= -nr_2\sin (nt+ \phi _2)$ we find after second-order averaging:

$$\begin{aligned} {\left\{ \begin{array}{ll} {\dot{r}}_1 = O(\varepsilon ^3), {\dot{r}}_2 = O(\varepsilon ^3), \\ {\dot{\phi }}_1 = \varepsilon ^2 \frac{r_2^2}{m(m^2-4n^2)} + O(\varepsilon ^3),\\ {\dot{\phi }}_2 = \varepsilon ^2 \frac{r_1^2}{n(m^2-4n^2)} + \varepsilon ^2 \frac{(8n^2-3m^2)}{4m^2n(m^2-4n^2)}r_2^2 + O(\varepsilon ^3). \end{array}\right. } \end{aligned}$$

(41)

For the combination angle $\chi = n \phi _1- m \phi _2$, we find to $O(\varepsilon ^2)$:

$$\begin{aligned} {\dot{\chi }} = \varepsilon ^2 \frac{m}{n(m^2-4n^2)} \left( \frac{3m^2-4n^2}{4m^2}r_2^2 -r_1^2 \right) + \dots \end{aligned}$$

(42)

Putting the right-hand side of (42) zero and using the energy integral

$$\begin{aligned} \frac{1}{2}(m^2r_1^2+n^2r_2^2)= = E_0, \end{aligned}$$

we find for the location of a resonance manifold M the values:

$$\begin{aligned} r_1^2= \frac{3m^2- 4n^2}{3m^4}2E_0,\, r_2^2= \frac{8}{3m^2}E_0. \end{aligned}$$

(43)

So, for the existence of a resonance manifold, we have the requirement:

$$\begin{aligned} \frac{m}{n} > \frac{2}{3} \sqrt{3}. \end{aligned}$$

(44)

From the Hamiltonian at higher order resonance (35), we have apart from the $r_1, r_2$ values (43) the values $\chi = 0, \pi$. In physical space, this leads by elimination of the goniometric expressions to polynomial relations between x(t) and y(t).

Examples are shown in Fig. 10 for the $m:n= 4:1, 5:2$ and 7 : 3 resonances. The initial conditions were obtained from Eq. (43) with $\chi (0)=0, E_0= 0.1$.

The resonance domains have, respectively, the sizes $O(\varepsilon ^{\frac{1}{2}}), O(\varepsilon ^{\frac{3}{2}})$ and $O(\varepsilon ^{3})$. The larger $m+n$, the longer the time interval of interaction in the resonance domain. More details can be found in [22].

11 Discussion and conclusions

Considering the scientific literature, one observes that the use of asymptotic series to approximate solutions of differential equations takes all kind of different forms: averaging, multiple timing, harmonic balance, renormalisation, WKBJ, etc., see [30]. Averaging is the only method with explicit error estimates and intervals of validity for first- and higher order approximations. Multiple timing is, with the right conditions, correct at first order but has counterexamples for higher order. Harmonic balance is a method without any foundation or justification, see [24], ch. 9. The choice of a particular method seems to be often a matter of taste. In this respect, it is very important for well-founded research to have comparative and unifying studies as [19, 16, 17, 23] and [2, 3], to name a few.

Conclusions

• Initial value problems with a small parameter may involve timelike variables as $t, \varepsilon t$, in general $\varepsilon ^n t, n=1, 2, \dots$. In the interesting case of qualitative changes, tipping points and bifurcations, algebraic timelike variables may arise. This occurs already in linear problems with eigenvalues causing structural instability.

• Oscillating systems where we can identify 2 or more angles can contain resonance manifolds. We have seen such problems in dissipative and in Hamiltonian systems. The quantitative description of these resonance manifolds require again higher order algebraic timescales and asymptotically small domains

• It is essential to use approximation methods that do not anticipate the timelike variables that are relevant for the approximations. These variables present themselves naturally in the course of the analysis for normal form methods and averaging.

In engineering, there is a trend to consider exclusively numerical methods to solve problems. This is useful for a number of isolated practical problems where one looks for numbers only and not for theoretical insight. Think of the design of a building structure of given dimensions. See also the comments in [6].

For general theoretical insight, it is important to have the use of both analytical and numerical, computational methods. Note that validation of results by numerics is possible only for isolated cases, general validation of results and methods require mathematical analysis. A recent, rather simple example of this approach is [1], where Neimark-Sacker bifurcation is analysed for interaction of a self-excited and a parametrically excited oscillator. It turns out that its simple formulation is deceptive, numerical explorations show various phenomena. These results inspire the asymptotic analysis that yield values of the parameters that produce families of quasi-periodic solutions that are organised on tori surrounding periodic solutions. In its turn, the analysis suggests more numerical illustrations.

Advanced numerical methods and high speed computers are available for research problems; the following strategy can be useful:

A hybrid strategy

• 1. Start with a few numerical explorations.

• 2. Identify parameters and use asymptotic expansions to obtain more general insight.

• 3. Use numerical bifurcation programs like Auto and Matcont to extend general insight.

• 4. Summarise the information in pictures typical for the dynamics.