Skip to main content
SpringerLink
Log in

Nonlinear dynamic behavior analysis of an elastically restrained double-beam connected through a mass-spring system that is nonlinear

  • Original Paper
  • Published:
Nonlinear Dynamics Aims and scope Submit manuscript

Abstract

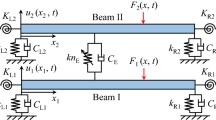
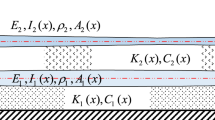
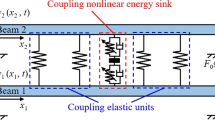
Some complex engineering structures can be modeled as multiple beams connected through coupling elements. When the coupling element is elastic, it can be simplified as a mass-spring system. The existing studies mainly concentrated on the double-beam coupled through elastic connectors, where the connector is simplified as the equivalent linear stiffness element or linear mass-spring system. Furthermore, many researches ignore rotational boundary restraints in analyzing dynamic behavior of the double-beam connected through elastic connectors, limiting their engineering generality. Considering the above limitations, this study attempts to employ the cubic nonlinear stiffness in the coupling mass-spring system and study the potential application of the mass-spring system that is nonlinear on the vibration control of the double-beam system. Using the variational method and the generalized Hamiltonian method build the corresponding system’s governing functions. Applying the Galerkin truncation method (GTM) obtains the dynamic behavior of the double-beam connected through a mass-spring system that is nonlinear. According to this study, the change of the mass-spring system that is nonlinear significantly influences the dynamic behavior of the double-beam system, where the complex dynamic behavior occurs under certain parameters of the mass-spring system that is nonlinear. Suitable parameters of the mass-spring system that is nonlinear are good at the vibration suppression at the boundary of the vibration system. Furthermore, the mass-spring system that is nonlinear can change the characteristics of the double-beam system’s kinetic energy transfer. For the vibration model established in this work, a quasi-periodic vibration state can be regarded as a sign of the occurrence of the targeted energy transfer of the double-beam connected through a mass-spring system that is nonlinear.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16

Similar content being viewed by others

Data availability

The datasets generated during and/or analyzed during the current study are available from the corresponding author upon reasonable request.

References

  1. Kang, K.H., Kim, K.J.: Modal properties of beams and plates on resilient supports with rotational and translational complex stiffness[J]. J. Sound Vib. 190(2), 207–220 (1996)

    Article  Google Scholar 

  2. Kim, H.K., Kim, M.S.: Vibration of beams with generally restrained boundary conditions using Fourier series[J]. J. Sound Vib. 245(5), 771–784 (2001)

    Article  Google Scholar 

  3. Li, W.L.: Free vibrations of beams with general boundary conditions[J]. J. Sound Vib. 237(4), 709–725 (2000)

    Article  MathSciNet  Google Scholar 

  4. Li, W.L., Zhang, X.F., Du, J.T., Liu, Z.G.: An exact series solution for the transverse vibration of rectangular plates with general elastic boundary supports[J]. J. Sound Vib. 321, 254–269 (2009)

    Article  Google Scholar 

  5. Ye, T.G., Jin, G.Y., Ye, X.M., Wang, X.R.: A series solution for the vibrations of composite laminated deep curved beams with general boundaries[J]. Compos. Struct. 127, 450–465 (2015)

    Article  Google Scholar 

  6. Wang, Q.S., Shi, D.Y., Liang, Q.: Free vibration analysis of axially loaded laminated composite beams with generally boundary conditions by using a modified Fourier-Ritz approach[J]. J. Compos. Mater. 50(15), 2111–2135 (2016)

    Article  Google Scholar 

  7. Chen, Q., Du, J.T.: A Fourier series solution for the transverse vibration of rotating beams with elastic boundary supports[J]. Appl. Acoust. 155, 1–15 (2019)

    Article  Google Scholar 

  8. Wang, Y.H., Du, J.T., Cheng, L.: Power flow and structural intensity analyses of Acoustic Black Hole beams. Mech. Syst. Signal Process. 131, 538–553 (2019)

    Article  Google Scholar 

  9. Xu, D.S., Du, J.T., Zhao, Y.H.: Flexural vibration and power flow analyses of axially loaded beams with general boundary and non-uniform elastic foundations[J]. Adv. Mech. Eng. 12(5), 1–14 (2020)

    Article  Google Scholar 

  10. Xu, D.S., Du, J.T., Tian, C.: Vibration characteristics and power flow analyses of a ship propulsion shafting system with general support and thrust loading. Shock Vib. 2020, 1–13 (2020)

    Article  Google Scholar 

  11. Özhan, B.B., Pakdemirli, M.: A general solution procedure for the forced vibrations of a system with cubic nonlinearities: three-to-one internal resonances with external excitation. J. Sound Vib. 329, 2603–2615 (2010)

    Article  Google Scholar 

  12. Ghayesh, M.H., Kazemirad, S., Darabi, M.A.: A general solution procedure for vibrations of systems with cubic nonlinearities and nonlinear/time-dependent internal boundary conditions. J. Sound Vib. 330, 5382–5400 (2011)

    Article  Google Scholar 

  13. Ghayesh, M.H., Kazemirad, S., Reid, T.: Nonlinear vibrations and stability of parametrically exited systems with cubic nonlinearities and internal boundary conditions: a general solution procedure. Appl. Math. Model. 36(7), 3299–3311 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  14. Wang, Y.R., Fang, Z.W.: Vibrations in an elastic beam with nonlinear supports at both ends. J. Appl. Mech. Tech. Phys. 56(2), 337–346 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  15. Mao, X.Y., Ding, H., Chen, L.Q.: Vibration of flexible structures under nonlinear boundary conditions. J. Appl. Mech. 84(11), 111006 (2017)

    Article  Google Scholar 

  16. Tang, B., Brennan, M.J., Manconi, E.: On the use of the phase closure principle to calculate the natural frequencies of a rod or beam with nonlinear boundaries. J. Sound Vib. 433, 461–475 (2018)

    Article  Google Scholar 

  17. Ding, H., Zhu, M.H., Chen, L.Q.: Nonlinear vibration isolation of a viscoelastic beam. Nonlinear Dyn. 92, 325–349 (2018)

    Article  Google Scholar 

  18. Ding, H., Lu, Z.Q., Chen, L.Q.: Nonlinear isolation of transverse vibration of pre-pressure beams. J. Sound Vib. 442, 738–751 (2019)

    Article  Google Scholar 

  19. Ding, H., Chen, L.Q.: Nonlinear vibration of a slightly curved beam with quasi-zero-stiffness isolators. Nonlinear Dyn. 95, 2367–2382 (2019)

    Article  MATH  Google Scholar 

  20. Zhao, Y.H., Du, J.T.: Dynamic behavior of an axially loaded beam supported by a mass-spring system that is nonlinear. Int. J. Struct. Stab. Dyn. 2021, 2150152 (2021)

    Article  Google Scholar 

  21. Georgiades, F., Vakakis, A.F.: Dynamics of a linear beam with an attached local nonlinear energy sink. Commun. Nonlinear Sci. Numer. Simul. 12, 643–651 (2007)

    Article  MATH  Google Scholar 

  22. Ahmadabadi, Z.N., Khadem, S.E.: Nonlinear vibration control of a cantilever beam by a nonlinear energy sink. Mech. Mach. Theory 50, 134–149 (2012)

    Article  Google Scholar 

  23. Ahmadabadi, Z.N., Khadem, S.E.: Nonlinear vibration control and energy harvesting of a beam using a nonlinear energy sink and a piezoelectric device. J. Sound Vib. 333, 4444–4457 (2014)

    Article  Google Scholar 

  24. Kani, M., Khadem, S.E., Pashaei, M.H., Dardel, M.: Vibration control of a nonlinear beam with a nonlinear energy sink. Nonlinear Dyn. 83, 1–22 (2015)

    Article  MathSciNet  Google Scholar 

  25. Parseh, M., Dardel, M., Ghasemi, M.H.: Investigating the robustness of nonlinear energy sink in steady state dynamics of linear beams with different boundary conditions. Commun. Nonlinear Sci. Numer. Simul. 29, 50–71 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  26. Kani, M., Khadem, S.E., Pashaei, M.H., Dardel, M.: Design and performance analysis of a nonlinear energy sink attached to a beam with different support conditions. J. Mech. Eng. Sci. 230(4), 527–542 (2015)

    Article  Google Scholar 

  27. Parseh, M., Dardel, M., Ghasemi, M.H., Pashaei, M.H.: Steady state dynamics of a non-linear beam coupled to a non-linear energy sink. Int. J. Non-Linear Mech. 79, 48–65 (2016)

    Article  Google Scholar 

  28. Chen, J.E., He, W., Zhang, W., Yao, M.H., Liu, J., Sun, M.: Vibration suppression and higher branch responses of beam with parallel nonlinear energy sinks. Nonlinear Dyn. 91, 885–904 (2018)

    Article  Google Scholar 

  29. Zhang, Y.W., Hou, S., Xu, K.F., Yang, T.Z., Chen, L.Q.: Forced vibration control of an axially moving beam with an attached nonlinear energy sink. Acta Mech. Sol. Sin. 30, 674–682 (2017)

    Article  Google Scholar 

  30. Zhang, Z., Ding, H., Zhang, Y.W., Chen, L.Q.: Vibration suppression of an elastic beam with boundary inerter-enhanced nonlinear energy sinks. Acta Mech. Sol. Sin. 37(3), 387–401 (2021)

    Article  MathSciNet  Google Scholar 

  31. Oniszczuk, Z.: Free transverse vibrations of elastically connected simply supported double-beam complex system. J. Sound Vib. 232(2), 387–403 (2000)

    Article  Google Scholar 

  32. Gurgoze, M., Erdogan, G., Inceoglu, S.: Bending vibrations of beams coupled by a double spring-mass system. J. Sound Vib. 243(2), 361–369 (2001)

    Article  Google Scholar 

  33. Pajand, M.R., Hozhabrossadati, S.M.: Free vibration analysis of a double-beam system joined by a mass-spring device. J. Vib. Control 22(13), 3004–3017 (2014)

    Article  MathSciNet  Google Scholar 

  34. Hilal, M.A.: Dynamic response of a double Euler-Bernoulli beam due to a moving constant load. J. Sound Vib. 297, 477–491 (2006)

    Article  Google Scholar 

  35. Li, J., Hua, H.X.: Spectral finite element analysis of elastically connected double-beam systems. Finite Elem. Anal. Des. 43, 1155–1168 (2007)

    Article  MathSciNet  Google Scholar 

  36. Rosa, M.A.D., Lippiello, M.: Non-classical boundary conditions and DQM for double-beams. Mech. Res. Commun. 34, 538–544 (2007)

    Article  MATH  Google Scholar 

  37. Zhang, Y.Q., Lu, Y., Wang, S.L., Liu, X.: Vibration and buckling of a double-beam system under compressive axial loading. J. Sound Vib. 318, 341–352 (2008)

    Article  Google Scholar 

  38. Stojanovic, V., Kozic, P., Paviovic, R., Janevski, G.: Effect of rotary inertia and shear on vibration and buckling of a double beam system under compressive axial loading. Arch. Appl. Mech. 81, 1993–2005 (2011)

    Article  MATH  Google Scholar 

  39. Kozic, P., Pavlovic, R., Karlicic, D.: The flexural vibration and buckling of the elastically connected parallel-beams with a Kerr-type layer in between. Mech. Res. Commun. 56, 83–89 (2014)

    Article  Google Scholar 

  40. Palmeri, A., Adhikari, S.: A Galerkin-type state-space approach for transverse vibrations of slender double-beam systems with viscoelastic inner layer. J. Sound Vib. 330, 6372–6386 (2011)

    Article  Google Scholar 

  41. Mao, Q.B.: Free vibration analysis of elastically connected multiple-beams by using the Adomian modified decomposition method. J. Sound Vib. 331, 2532–2542 (2012)

    Article  Google Scholar 

  42. Mao, Q.B.: Vibration and stability of a double-beam system interconnected by an elastic foundation under conservative and nonconservative axial forces. Int. J. Mech. Sci. 93, 1–7 (2015)

    Article  Google Scholar 

  43. Mohammadi, N., Nasirshoaibi, M.: Forced transverse vibration analysis of a Rayleigh double-beam system with a Pasternak middle layer subjected to compressive axial load. J. Vibroeng. 17(8), 4545–4559 (2015)

    Google Scholar 

  44. Pisarski, D., Szmidt, T., Bajer, C., Dyniewicz, B., Bajkowski, J.M.: Vibration control of double-beam system with multiple smart damping members. Shock Vib. 2016, 1–14 (2016)

    Article  Google Scholar 

  45. Fei, H., Danhui, D., Cheng, W., Jia, P.F.: Analysis on the dynamic characteristic of a tensioned double-beam system with a semi theoretical semi numerical method. Compos. Struct. 185(1), 584–599 (2018)

    Article  Google Scholar 

  46. O.O. Agboola, J.A. Gbadeyan, S.A. Iyase. Effects of some structural parameters on the vibration of a simply supported non-prismatic double-beam system. Proceedings of the World Congress on Engineering, 2017, IWCE, Vol I, London, UK

  47. Rahman, M.S., Lee, Y.Y.: New modified multi-level residue harmonic balance method for solving nonlinearly vibrating double-beam problem. J. Sound Vib. 406, 295–327 (2017)

    Article  Google Scholar 

  48. Lee, J., Wang, S.Y.: Vibration analysis of a partially connected double-beam system with the transfer matrix method and identification of the slap phenomenon in the system. Int. J. Appl. Mech. 9(7), 1750093 (2017)

    Article  Google Scholar 

  49. Chen, L.J., Xu, D.S., Du, J.T., Zhong, C.W.: Flexural vibration analysis of nonuniform double-beam system with general boundary and coupling conditions. Shock Vib. 2018, 1–8 (2018)

    Google Scholar 

  50. Hao, Q.J., Zhai, W.J., Chen, Z.B.: Free vibration of connected double-beam system with general boundary conditions by a modified Fourier-Ritz method. Arch. Appl. Mech. 88, 741–754 (2018)

    Article  Google Scholar 

  51. Zhao, X.Z., Asce, P.E.M.: Solution to vibrations of double-Beam systems under general boundary conditions. J. Eng. Mech. 147(10), 04021073 (2021)

    Google Scholar 

  52. Li, Y.X., Xiong, F., Xie, L.Z., Sun, L.Z.: State-space approach for transverse vibration of double-beam systems. Int. J. Mech. Sci. 189, 105974 (2021)

    Article  Google Scholar 

  53. Pajand, M.R., Sani, A.A., Hozhabrossadati, S.M.: Analyzing free vibration of a double-beam joined by a three-degree of freedom system. J. Braz. Soc. Mech. Sci. Eng. 41, 211 (2019)

    Article  Google Scholar 

  54. Guo, T.D., Kang, H.J., Wang, L.H., Zhao, Y.Y.: Nonlinear vibrations for double inclined cables–deck beam coupled system using asymptotic reductions. Int. J. Non-Linear Mech. 108, 33–45 (2019)

    Article  Google Scholar 

  55. Stojanovic, V., Petkovic, M.D., Milic, D.: Nonlinear vibrations of a coupled beam-arch bridge system. J. Sound Vib. 464(4), 115000 (2020)

    Article  Google Scholar 

Download references

Funding

This work is supported by the National Natural Science Foundation of China (Grant No. 11972125 and 12102101).

Author information

Authors and Affiliations

  1. College of Power and Energy Engineering, Harbin Engineering University, Harbin, 150001, People’s Republic of China

    Yuhao Zhao, Jingtao Du, Yilin Chen & Yang Liu

Authors
  1. Yuhao Zhao
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Jingtao Du
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Yilin Chen
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Yang Liu
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Yang Liu.

Ethics declarations

Conflict of interest

The authors declare no conflict of interest in preparing this article.

Human or animal rights

No human or animal subjects were used in this work.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Appendices

Appendix A

$$ V_{{{\text{Beam}}I}} = \int_{0}^{{L_{1} }} {\frac{1}{2}E_{1} I_{1} } \left( {\frac{{\partial^{2} u_{1} }}{{\partial x_{1}^{2} }}} \right)^{2} {\text{d}} x_{1} $$
(A1)
$$ V_{BeamII} = \int_{0}^{{L_{2} }} {\frac{1}{2}E_{2} I_{2} } \left( {\frac{{\partial^{2} u_{2} }}{{\partial x_{2}^{2} }}} \right)^{2} {\text{d}} x_{2} $$
(A2)
$$ \begin{aligned} V_{BoundaryI} = & \frac{1}{2}k_{L1} \left[ {u_{1} \left( {0,t} \right)} \right]^{2} + \frac{1}{2}k_{R1} \left[ {u_{1} \left( {L_{1} ,t} \right)} \right]^{2} \\ & + \frac{1}{2}K_{L1} \left[ {\frac{{\partial u_{1} \left( {0,t} \right)}}{{\partial x_{1} }}} \right]^{2} + \frac{1}{2}K_{R1} \left[ {\frac{{\partial u_{1} \left( {L_{1} ,t} \right)}}{{\partial x_{1} }}} \right]^{2} \\ \end{aligned} $$
(A3)
$$ \begin{aligned} V_{BoundaryII} = & \frac{1}{2}k_{{{\text{L}} 2}} \left[ {u_{2} \left( {0,t} \right)} \right]^{2} + \frac{1}{2}k_{R2} \left[ {u_{2} \left( {L_{2} ,t} \right)} \right]^{2} \\ & + \frac{1}{2}K_{L2} \left[ {\frac{{\partial u_{2} \left( {0,t} \right)}}{{\partial x_{2} }}} \right]^{2} + \frac{1}{2}K_{R2} \left[ {\frac{{\partial u_{2} \left( {L_{2} ,t} \right)}}{{\partial x_{2} }}} \right]^{2} \\ \end{aligned} $$
(A4)
$$ \begin{aligned} V_{E} = & \frac{1}{2}k_{E1} \left[ {u_{E} - u_{1} \left( {x_{E1} ,t} \right)} \right]^{2} + \frac{1}{2}k_{E2} \left[ {u_{E} - u_{2} \left( {x_{E2} ,t} \right)} \right]^{2} \\ & \frac{1}{4}kn_{E1} \left[ {u_{E} - u_{1} \left( {x_{E1} ,t} \right)} \right]^{4} + \frac{1}{4}kn_{E2} \left[ {u_{E} - u_{2} \left( {x_{E2} ,t} \right)} \right]^{4} \\ \end{aligned} $$
(A5)
$$ T_{I} = \int_{0}^{{L_{1} }} {\frac{1}{2}\rho_{1} S_{1} } \left( {\frac{{\partial u_{1} }}{\partial t}} \right)^{2} {\text{d}} t $$
(A6)
$$ T_{II} = \int_{0}^{{L_{2} }} {\frac{1}{2}\rho_{2} S_{2} } \left( {\frac{{\partial^{2} u_{2} }}{{\partial t^{2} }}} \right)^{2} {\text{d}} t $$
(A7)
$$ T_{E} = \frac{1}{2}m_{E} \left( {\frac{{{\text{d}} u_{E} }}{{{\text{d}} t}}} \right)^{2} $$
(A8)
$$ \delta W_{C1} = - \int_{0}^{{L_{1} }} {C_{B1} } \frac{{\partial u_{1} }}{\partial t}\delta u_{1} {\text{d}} x_{1} $$
(A9)
$$ \delta W_{C2} = - \int_{0}^{{L_{2} }} {C_{B2} } \frac{{\partial u_{2} }}{\partial t}\delta u_{2} {\text{d}} x_{2} $$
(A10)
$$ \delta W_{CE1} = - C_{E1} \left[ {\frac{{\partial u_{E} }}{\partial t} - \frac{{\partial u_{1} \left( {x_{E1} ,t} \right)}}{\partial t}} \right]\delta \left[ {u_{E} - u_{1} \left( {x_{E1} ,t} \right)} \right] $$
(A11)
$$ \delta W_{CE2} = - C_{E2} \left[ {\frac{{\partial u_{E} }}{\partial t} - \frac{{\partial u_{2} \left( {x_{E2} ,t} \right)}}{\partial t}} \right]\delta \left[ {u_{E} - u_{2} \left( {x_{E2} ,t} \right)} \right] $$
(A12)
$$ \delta W_{F1} = - \int_{0}^{{L_{1} }} {\delta \left( {x_{1} - L_{1} } \right)F_{1} \sin \left( {\omega t} \right)} \delta u_{1} {\text{d}} x_{1} $$
(A13)

Appendix B

$$ \begin{aligned} \int_{{t_{1} }}^{{t_{2} }} {\delta V_{{{\text{Beam}}I}} {\text{d}} t} = & \int_{{t_{1} }}^{{t_{2} }} {\int_{0}^{{L_{1} }} {E_{1} I_{1} \frac{{\partial^{4} u_{1} }}{{\partial x_{1}^{4} }}} \delta u_{1} {\text{d}} x_{1} {\text{d}} t} \\ & + \int_{{t_{1} }}^{{t_{2} }} {\left[ \begin{gathered} E_{1} I_{1} \frac{{\partial^{2} u_{1} \left( {L_{1} ,t} \right)}}{{\partial x_{1}^{2} }}\delta \left( {\frac{{\partial u_{1} }}{{\partial x_{1} }}} \right) - E_{1} I_{1} \frac{{\partial^{3} u_{1} \left( {L_{1} ,t} \right)}}{{\partial x_{1}^{3} }}\delta u_{1} \hfill \\ - E_{1} I_{1} \frac{{\partial^{2} u_{1} \left( {0,t} \right)}}{{\partial x_{1}^{2} }}\delta \left( {\frac{{\partial u_{1} }}{{\partial x_{1} }}} \right) + E_{1} I_{1} \frac{{\partial^{3} u_{1} \left( {0,t} \right)}}{{\partial x_{1}^{3} }}\delta u_{1} \hfill \\ \end{gathered} \right]} {\text{d}} t \\ \end{aligned} $$
(B1)
$$ \begin{aligned} \int_{{t_{1} }}^{{t_{2} }} {\delta V_{BeamII} {\text{d}} t} = & \int_{{t_{1} }}^{{t_{2} }} {\int_{0}^{{L_{2} }} {E_{2} I_{2} \frac{{\partial^{4} u_{2} }}{{\partial x_{2}^{4} }}} \delta u_{2} {\text{d}} x_{2} {\text{d}} t} \\ & + \int_{{t_{1} }}^{{t_{2} }} {\left[ \begin{gathered} E_{2} I_{2} \frac{{\partial^{2} u_{2} \left( {L_{2} ,t} \right)}}{{\partial x_{2}^{2} }}\delta \left( {\frac{{\partial u_{2} }}{{\partial x_{2} }}} \right) - E_{2} I_{2} \frac{{\partial^{3} u_{2} \left( {L_{2} ,t} \right)}}{{\partial x_{2}^{3} }}\delta u_{2} \hfill \\ - E_{2} I_{2} \frac{{\partial^{2} u_{2} \left( {0,t} \right)}}{{\partial x_{2}^{2} }}\delta \left( {\frac{{\partial u_{2} }}{{\partial x_{2} }}} \right) + E_{2} I_{2} \frac{{\partial^{3} u_{2} \left( {0,t} \right)}}{{\partial x_{2}^{3} }}\delta u_{2} \hfill \\ \end{gathered} \right]} {\text{d}} t \\ \end{aligned} $$
(B2)
$$ \int_{{t_{1} }}^{{t_{2} }} {\delta V_{BoundaryI} {\text{d}} t} = \int_{{t_{1} }}^{{t_{2} }} {\left[ \begin{gathered} \begin{array}{*{20}c} {} \\ \end{array} k_{L1} u_{1} \left( {0,t} \right)\delta u_{1} + K_{L1} \frac{{\partial u_{1} \left( {0,t} \right)}}{{\partial x_{1} }}\delta \left( {\frac{{\partial u_{1} }}{{\partial x_{1} }}} \right) \hfill \\ + k_{R1} u_{1} \left( {L_{1} ,t} \right)\delta u_{1} + K_{R1} \frac{{\partial u_{1} \left( {L_{1} ,t} \right)}}{{\partial x_{1} }}\delta \left( {\frac{{\partial u_{1} }}{{\partial x_{1} }}} \right) \hfill \\ \end{gathered} \right]{\text{d}} t} $$
(B3)
$$ \int_{{t_{1} }}^{{t_{2} }} {\delta V_{BoundaryII} {\text{d}} t} = \int_{{t_{1} }}^{{t_{2} }} {\left[ \begin{gathered} \begin{array}{*{20}c} {} \\ \end{array} k_{L2} u_{2} \left( {0,t} \right)\delta u_{2} + K_{L2} \frac{{\partial u_{2} \left( {0,t} \right)}}{{\partial x_{2} }}\delta \left( {\frac{{\partial u_{2} }}{{\partial x_{2} }}} \right) \hfill \\ + k_{R2} u_{2} \left( {L_{2} ,t} \right)\delta u_{2} + K_{R2} \frac{{\partial u_{2} \left( {L_{2} ,t} \right)}}{{\partial x_{2} }}\delta \left( {\frac{{\partial u_{2} }}{{\partial x_{2} }}} \right) \hfill \\ \end{gathered} \right]} {\text{d}} t $$
(B4)
$$ \int_{{t_{1} }}^{{t_{2} }} {\delta V_{E} {\text{d}} t} = \int_{{t_{1} }}^{{t_{2} }} {\left\{ \begin{gathered} \begin{array}{*{20}c} {} \\ \end{array} k_{E1} \left[ {u_{E} - u_{1} \left( {x_{E1} ,t} \right)} \right]\delta \left[ {u_{E} - u_{1} \left( {x_{E1} ,t} \right)} \right] \hfill \\ + k_{E2} \left[ {u_{E} - u_{2} \left( {x_{E2} ,t} \right)} \right]\delta \left[ {u_{E} - u_{2} \left( {x_{E2} ,t} \right)} \right] \hfill \\ + kn_{E1} \left[ {u_{E} - u_{1} \left( {x_{E1} ,t} \right)} \right]^{3} \delta \left[ {u_{E} - u_{1} \left( {x_{E1} ,t} \right)} \right] \hfill \\ + kn_{E2} \left[ {u_{E} - u_{2} \left( {x_{E2} ,t} \right)} \right]^{3} \delta \left[ {u_{E} - u_{2} \left( {x_{E2} ,t} \right)} \right] \hfill \\ \end{gathered} \right\}{\text{d}} t} $$
(B5)
$$ \int_{{t_{1} }}^{{t_{2} }} {\delta T_{I} {\text{d}} t = } - \int_{{t_{1} }}^{{t_{2} }} {\int_{0}^{{L_{1} }} {\rho_{1} S_{1} \frac{{\partial^{2} u_{1} }}{\partial t}} } \delta u_{1} {\text{d}} x_{1} {\text{d}} t $$
(B6)
$$ \int_{{t_{1} }}^{{t_{2} }} {\delta T_{II} {\text{d}} t = } - \int_{{t_{1} }}^{{t_{2} }} {\int_{0}^{{L_{2} }} {\rho_{2} S_{2} \frac{{\partial^{2} u_{2} }}{\partial t}} } \delta u_{2} {\text{d}} x_{2} {\text{d}} t $$
(B7)
$$ \int_{{t_{1} }}^{{t_{2} }} {\delta T_{E} {\text{d}} t} = - \int_{{t_{1} }}^{{t_{2} }} {m_{E} \frac{{{\text{d}}^{2} u_{\text{E}} }}{{{\text{d}} t^{2} }}\delta u_{E} } {\text{d}} t $$
(B8)
$$ \int_{{t_{1} }}^{{t_{2} }} {\delta W_{C1} {\text{d}} t} = - \int_{{t_{1} }}^{{t_{2} }} {\int_{0}^{{L_{1} }} {C_{B1} } \frac{{\partial u_{1} }}{\partial t}\delta u_{1} {\text{d}} x_{1} {\text{d}} t} $$
(B9)
$$ \int_{{t_{1} }}^{{t_{2} }} {\delta W_{C2} {\text{d}} t} = - \int_{{t_{1} }}^{{t_{2} }} {\int_{0}^{{L_{2} }} {C_{B2} } \frac{{\partial u_{2} }}{\partial t}\delta u_{2} {\text{d}} x_{2} {\text{d}} t} $$
(B10)
$$ \int_{{t_{1} }}^{{t_{2} }} {\delta W_{CE1} {\text{d}} t} = - \int_{{t_{1} }}^{{t_{2} }} {C_{E1} \left[ {\frac{{{\text{d}} u_{E} }}{{{\text{d}} t}} - \frac{{\partial u_{1} \left( {x_{E1} ,t} \right)}}{\partial t}} \right]\delta \left[ {u_{E} - u_{1} \left( {x_{E1} ,t} \right)} \right]{\text{d}} t} $$
(B11)
$$ \int_{{t_{1} }}^{{t_{2} }} {\delta W_{CE2} {\text{d}} t} = - \int_{{t_{1} }}^{{t_{2} }} {C_{E2} \left[ {\frac{{{\text{d}} u_{E} }}{{{\text{d}} t}} - \frac{{\partial u_{2} \left( {x_{E2} ,t} \right)}}{\partial t}} \right]\delta \left[ {u_{E} - u_{2} \left( {x_{E2} ,t} \right)} \right]{\text{d}} t} $$
(B12)
$$ \int_{{t_{1} }}^{{t_{2} }} {\delta W_{F1} {\text{d}} t} = - \int_{{t_{1} }}^{{t_{2} }} {\int_{0}^{{L_{1} }} {\delta \left( {x_{1} - L_{1} } \right)F_{1} \sin \left( {\omega t} \right)} \delta u_{1} {\text{d}} x_{1} {\text{d}} t} $$
(B13)

Appendix C

$$ RI_{{m_{1} 1}} = \int_{0}^{{L_{1} }} {\rho_{1} S_{1} \left[ {\sum\limits_{{{\text{i}} = 1}}^{{{\text{N}}_{1} }} {\varphi_{1i} \left( {x_{1} } \right)\frac{{{\text{d}}^{2} q_{1i} \left( t \right)}}{{{\text{d}} t^{2} }}} } \right]\psi_{{1m_{1} }} \left( {x_{1} } \right){\text{d}} x_{1} } $$
(C1)
$$ RI_{{m_{1} 2}} = \int_{0}^{{L_{1} }} {C_{{{\text{B}} 1}} \left[ {\sum\limits_{{{\text{i}} = 1}}^{{{\text{N}}_{1} }} {\varphi_{1i} \left( {x_{1} } \right)\frac{{{\text{d}} q_{1i} \left( t \right)}}{{{\text{d}} t}}} } \right]\psi_{{1m_{1} }} \left( {x_{1} } \right){\text{d}} x_{1} } $$
(C2)
$$ RI_{{m_{1} 3}} = \int_{0}^{{L_{1} }} {E_{1} I_{1} \left[ {\sum\limits_{{{\text{i}} = 1}}^{{{\text{N}}_{1} }} {\frac{{{\text{d}}^{4} \varphi_{1i} \left( x \right)}}{{{\text{d}} x_{1}^{4} }}q_{1i} \left( t \right)} } \right]\psi_{{1m_{1} }} \left( {x_{1} } \right){\text{d}} x_{1} } $$
(C3)
$$ RI_{{m_{1} 4}} = \psi_{{1m_{1} }} \left( {x_{F1} } \right)F_{1} \sin \left( {\omega t} \right) $$
(C4)
$$ RI_{{{\text{m}}_{1} {5}}} = C_{E1} \left[ {\sum\limits_{{{\text{i}} = 1}}^{{{\text{N}}_{1} }} {\varphi_{1i} \left( {x_{{{\text{E}} 1}} } \right)\frac{{{\text{d}} q_{1i} \left( t \right)}}{{{\text{d}} t}}} - u_{E} \left( t \right)} \right]\psi_{{1m_{1} }} \left( {x_{E1} } \right) $$
(C5)
$$ RI_{{{\text{m}}_{1} {6}}} = k_{E1} \left[ {\sum\limits_{{{\text{i}} = 1}}^{{{\text{N}}_{1} }} {\varphi_{1i} \left( {x_{E1} } \right)q_{1i} \left( t \right)} - u_{\text{E}} \left( t \right)} \right]\psi_{{1m_{1} }} \left( {x_{E1} } \right) $$
(C6)
$$ RI_{{{\text{m}}_{1} {7}}} = kn_{E1} \left[ {\sum\limits_{{{\text{i}} = 1}}^{{{\text{N}}_{1} }} {\varphi_{1i} \left( {x_{E1} } \right)q_{1i} \left( t \right)} - u_{\text{E}} \left( t \right)} \right]^{3} \psi_{{1m_{1} }} \left( {x_{E1} } \right) $$
(C7)
$$ RII_{{m_{2} 1}} = \int_{0}^{{L_{2} }} {\rho_{2} S_{2} \left[ {\sum\limits_{{{\text{i}} = 1}}^{{{\text{N}}_{2} }} {\varphi_{2i} \left( {x_{2} } \right)\frac{{{\text{d}}^{2} q_{2i} \left( t \right)}}{{{\text{d}} t}}} } \right]\psi_{{2m_{2} }} \left( {x_{2} } \right){\text{d}} x_{2} } $$
(C8)
$$ RII_{{m_{2} 2}} = \int_{0}^{{L_{2} }} {C_{{{\text{B}} 2}} \left[ {\sum\limits_{{{\text{i}} = 1}}^{{{\text{N}}_{2} }} {\varphi_{2i} \left( {x_{2} } \right)\frac{{{\text{d}} q_{2i} \left( t \right)}}{{{\text{d}} t}}} } \right]\psi_{{2m_{2} }} \left( {x_{2} } \right){\text{d}} x_{2} } $$
(C9)
$$ RII_{{m_{2} 3}} = \int_{0}^{{L_{2} }} {E_{2} I_{2} \left[ {\sum\limits_{{{\text{i}} = 1}}^{{{\text{N}}_{2} }} {\frac{{{\text{d}}^{4} \varphi_{2i} \left( {x_{2} } \right)}}{{{\text{d}} x_{2}^{4} }}q_{2i} \left( t \right)} } \right]\psi_{{2m_{2} }} \left( {x_{2} } \right){\text{d}} x_{2} } $$
(C10)
$$ RII_{{{\text{m}}_{2} {4}}} = C_{E2} \left[ {\sum\limits_{{{\text{i}} = 1}}^{{{\text{N}}_{2} }} {\varphi_{2i} \left( {x_{{{\text{E}} 2}} } \right)\frac{{{\text{d}} q_{2i} \left( t \right)}}{{{\text{d}} t}}} - u_{E} \left( t \right)} \right]\psi_{{2m_{2} }} \left( {x_{{{\text{E}} 2}} } \right) $$
(C11)
$$ RII_{{{\text{m}}_{2} 5}} = k_{E2} \left[ {\sum\limits_{{{\text{i}} = 1}}^{{{\text{N}}_{2} }} {\varphi_{2i} \left( {x_{E2} } \right)q_{2i} \left( t \right)} - u_{E} \left( t \right)} \right]\psi_{{2m_{2} }} \left( {x_{E2} } \right) $$
(C12)
$$ RII_{{{\text{m}}_{2} {6}}} = kn_{E2} \left[ {\sum\limits_{{{\text{i}} = 1}}^{{{\text{N}}_{2} }} {\varphi_{2i} \left( {x_{E2} } \right)q_{2i} \left( t \right)} - u_{E} \left( t \right)} \right]^{3} \psi_{{2m_{2} }} \left( {x_{E2} } \right) $$
(C13)

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Zhao, Y., Du, J., Chen, Y. et al. Nonlinear dynamic behavior analysis of an elastically restrained double-beam connected through a mass-spring system that is nonlinear. Nonlinear Dyn 111, 8947–8971 (2023). https://doi.org/10.1007/s11071-023-08351-8

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11071-023-08351-8

Keywords

Search

Navigation