Skip to main content
SpringerLink
Log in

Dynamic analysis of the variable stiffness support rotor system with elastic rings

  • Original Paper
  • Published:
Nonlinear Dynamics Aims and scope Submit manuscript

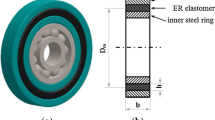
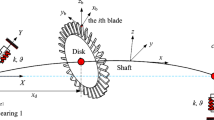
Abstract

Elastic rings are common rotor supporting structure, which have been widely used in aeroengine rotor support system. However, large inertia force and gyroscopic moment may occur during the operation of aeroengine, which may lead to contact between elastic ring and bearing pedestal, and then introduce variable stiffness into the rotor support system. In this paper, a mathematical model of variable stiffness of elastic ring is proposed and this model is subsequently verified by comparison with simulation analysis and experimental results. Based on this model, a variable stiffness model of an elastic ring-supported rotor is developed by coupling the kinetic equations of the rotor with the deformation of the combined support. Then, the spectrum cascades are used to analyze the dynamic characteristics of the rotor system. In addition, the influences of the variable stiffness of elastic ring on the critical speed of the system are also examined. Finally, some simulation results are verified by experiments on a combined test bench of an elastic ring-supported rotor.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13

Similar content being viewed by others

Data availability

Data will be made available on reasonable request.

Abbreviations

x, y :

Displacements in x and y directions

e :

Eccentricity

U i :

Displacement of inner bulges

i :

The ith inner bulge

n :

Number of rotor nodes

I :

Moment of inertia

E :

Elastic modulus

L :

Length of the ring section

b :

Width of the ring

h :

Thickness of the ring

F x, F y :

Force of each ring segment in the x and y directions

K 1 :

Linear segment of the elastic ring

K 2 :

Contact stiffness of the elastic ring

ΔR :

Radius difference between bearing pedestal and elastic ring

h min :

Minimum wall thickness of bearing pedestal

K er :

Variable stiffness of elastic ring

k b :

Stiffness of bearing

k sq :

Stiffness of squirrel cage

m i, m o :

Mass of the inner and outer race of the bearing

u s, u d :

Displacement vector of the shaft, displacement vector of the disk

Q s, Q d :

Excitation vector of the shaft, excitation vector of the disk

\( \boldsymbol{M}_{T}^{S},\boldsymbol{M}_{R}^{S}\) :

Translating inertial matrix of beam element, rotating inertial matrix of beam element

G s, \( \boldsymbol{K}_{B}^{S}\) :

Gyroscopic moment matrix of beam element, stiffness matrix of beam element

\( \boldsymbol{M}_{T}^{d}\), M d R, G d :

Translating inertial matrix of disk element, rotating inertial matrix of disk element, gyroscopic moment matrix of disk element

M r, G r :

Mass matrix of rotor substructure, gyroscopic matrix of rotor substructure

K r, C :

Stiffness matrix of rotor substructure, damping matrix of rotor substructure

F e, F b, F g :

Unbalance vector, bearing force vector, gravity vector

f n 1, f n 2 :

First and second natural frequency of the rotor system

ξ 1, ξ 2 :

First and second modal damping ratios

k B, k sq :

Contact stiffness of bearing, stiffness of squirrel cage

r 0, N b, θ j :

Bearing clearance, number of ball elements, angle location

x r, x o, y r, y o :

Translation of shaft and outer rings of the bearing along the x- and y-axes

w c :

Angular velocity of the cage

R b, r b :

Radius of outer race, radius of inner race

n sq, b sq, h sq, L sq :

Number of cage strips, section width of cage strips, section height of cage strips, length of cage strips

f er x, f er y :

Elastic ring force in the x and y directions

f sq x, f sq y :

Squirrel cage force in the x and y directions

F sq, F er, F b :

Squirrel cage force vector, elastic ring force vector, bearing force vector

Δ:

Height of the outer bulge

α :

Angle between inner and outer bulge

λ :

Flexibility

δ :

Depth of the contact

Ω:

Rotational speed

FE:

Finite element

DOF:

Degrees of freedom

ER:

Elastic rings

ERSFD:

Elastic ring squeeze film damper

References

  1. Li, L., Luo, Z., He, F.X., Zhe, D., Sun, K.: An improved partial similitude method for dynamic characteristic of rotor systems based on Levenberg–Marquardt method. Mech. Syst. Sig. Process. 165, 108405 (2022)

    Article  Google Scholar 

  2. Ma, Y.H., Zhu, H.X., Zhang, D.Y., Hong, J.: Experimental investigation on dynamic mechanical behavior of the elastic ring support with metal rubber. California (2013)

  3. Leontiev, M.K., Tereshko, A.G.: Research of characteristics of elastic rings mounted in rotor bearings of gas-turbine engines. Technical Report, Engineering & Consulting centre, Alfa Transit, Moscow Aviation Institute, Moscow (1998)

  4. Fu, C.G.: Aeroengine Manual, vol. 19. Aviation Industry Press, Beijing (2000)

    Google Scholar 

  5. Diligenskiy, D.S., Novikov, D.K.: Studying of manufacturing tolerance influence on the performance of GTE rotor elastic rings. Procedia Eng. 176, 483–497 (2017)

    Article  Google Scholar 

  6. Luo, Z., Li, L., Yang, Y., Ding, Z.: Experimental and numerical investigations on novel models for mechanical behaviors of the elastic ring in aero-engine. Proc IMechE, Part C: J. Mech. Eng. Sci. 235(22), 6257–6267 (2021)

    Article  Google Scholar 

  7. Guo, X.M., Ma, H., Zhang, X.F., Ye, Z., Fu, Q., Liu, Z.H., Han, Q.K.: Uncertain frequency responses of clamp-pipeline systems using an interval-based method. IEEE Acess. 8, 29370 (2020)

    Article  Google Scholar 

  8. Pereira, C.M., Ramalho, A.L., Ambrósio, J.A.: A critical overview of internal and external cylinder contact force models. Nonlinear Dyn. 63, 681–697 (2011)

    Article  Google Scholar 

  9. Machado, M., Moreira, P., Flores, P., Lankarani, H.M.: Compliant contact force models in multibody dynamics: Evolution of the Hertz contact theory. Mech. Mach. Theory. 53, 99–121 (2012)

    Article  Google Scholar 

  10. Persson, A.: On the Stress Distribution of Cylindrical Elastic Bodies in Contact. Chalmers University of Technology, Göteborg. (1964)

  11. Ciavarella, M., Decuzzi, P.: The state of stress induced by the plane frictionless cylindrical contact. I. The case of elastic similarity. International journal of solids and structures. 38(26), 4507–4523 (2001)

  12. Ciavarella, M., Decuzzi, P.: The state of stress induced by the plane frictionless cylindrical contact. II. The general case (elastic dissimilarity). International journal of solids and structures. 38(26), 4525–4533 (2001)

  13. Li, Y.T., Quan, Q.Q., Tang, D.W.: Modeling and experimental study of shaft hole coordinated contact. Journal of Harbin Engineering University. 37(11), 1546–1552 (2016)

    Google Scholar 

  14. Li, Y.Q., Luo, Z., Liu, J.X., Ma, H., Yang, D.S.: Dynamic modeling and stability analysis of a rotor-bearing system with bolted-disk joint. Mech. Syst. Signal Process. 158, 107778 (2021)

    Article  Google Scholar 

  15. Li, Y.Q., Luo, Z., Wang, J.W., Ma, H., Yang, D.S.: Numerical and experimental analysis of the effect of eccentric phase difference in a rotor-bearing system with bolted-disk joint[J]. Nonlinear Dyn. 105(3), 2105–2132 (2021)

    Article  Google Scholar 

  16. Sun, C., Chen, Y., Hou, L.: Steady-state response characteristics of a dual-rotor system induced by rub-impact. Nonlinear Dyn. 86(1), 91–105 (2016)

    Article  Google Scholar 

  17. Villa, C., Sinou, J.J., Thouverez, F.: Stability and vibration analysis of a complex flexible rotor bearing system. Commun. Nonlinear Sci. Numer. Simul. 13(4), 804–821 (2008)

    Article  Google Scholar 

  18. Hou, L., Chen, Y.S., Fu, Y.Q., Chen, H.Z., Lu, Z.Y., Liu, Z.S.: Application of the HB-AFT method to the primary resonance analysis of a dual-rotor system. Nonlinear Dyn. 88(4), 2531–2551 (2017)

    Article  Google Scholar 

  19. Luo, Z., Wang, J.W., Tang, R., Wang, D.Y.: Research on vibration performance of the nonlinear combined support-flexible rotor system. Nonlinear Dyn. 98(1), 113–128 (2019)

    Article  Google Scholar 

  20. Chen, G.: A new rotor-ball bearing-stator coupling dynamics model for whole aero-engine vibration. J. Vib. Acoust. 131, 061009 (2009)

    Article  Google Scholar 

  21. Zhang, W., Ding, Q.: Elastic ring deformation and pedestal contact status analysis of elastic ring squeeze film damper. J. Sound Vib. 346, 314–327 (2015)

    Article  Google Scholar 

  22. Wang, Z.L., Xu, N., Yu, X.Y., Liu, Z.S., Zhang, G.H.: The dynamic characteristic analysis of elastic ring squeeze film damper by fluid-structure interaction approach. Charlotte, NC, USA (2017)

  23. Wang, Z.L., Liu, Z.S., Zhang, G.H.: Dynamic characteristics of elastic ring squeeze film damper. Industrial Lubrication and Tribology. 71(10), 1144–1151 (2019)

    Article  Google Scholar 

  24. Chen, W.T., Chen, S.Y., Hu, Z.H., Tang, J.Y., Li, H.N.: A novel dynamic model for the spiral bevel gear drive with elastic ring squeeze film dampers. Nonlinear Dyn. 98(2), 1081–1105 (2019)

    Article  Google Scholar 

  25. Han, Z.F., Ding, Q., Zhang, W.: Dynamical analysis of an elastic ring squeeze film damper-rotor system. Mech. Mach. Theory. 131, 406–419 (2019)

    Article  Google Scholar 

  26. Han, Z.F., Ma, Z.S., Zhang, W., Han, B.B., Ding, Q.: Dynamic analysis of an elastic ring squeeze film damper supported rotor using a semi-analytic method. Eng. Appl. Comput. Fluid Mech. 14(1), 1263–1278 (2020)

    Article  Google Scholar 

  27. Chen, G.: Vibration modelling and verifications for whole aero-engine. J. Sound Vib. 349, 163–176 (2015)

    Article  Google Scholar 

  28. Li, L., Luo, Z., He, F.X., Zhao, X.Y., Liu, J.R.: A partial similitude method considering variable powers in scaling laws and applied to rotor-bearing systems. Int. J. Mech. Sci. 186, 105892 (2020)

    Article  Google Scholar 

  29. Chen, X., Ren, G.M., Gan, X.H.: Dynamic behavior of a flexible rotor system with squeeze film damper considering oil-film inertia under base motions: Nonlinear Dyn. 106, 3117–3145 (2021)

  30. Li, L., Luo, Z., He, F.X., Ding, Z., Sun, K.: A partial similitude method for vibration responses of rotor systems: Numerical and experimental verification. Int. J. Mech. Sci. 208, 106696 (2021)

    Article  Google Scholar 

  31. Yang, X.D., Zhang, W., Chen, L.Q., Yao, M.H.: Dynamical analysis of axially moving plate by finite difference method. Nonlinear Dyn. 67(2), 997–1006 (2012)

    Article  MathSciNet  Google Scholar 

  32. Liu, Y., Han, J.Y., Zhao, S.Y., Meng, Q.Y., Shi, T., Ma, H.: Study on the dynamic problems of double-disk rotor system supported by deep groove ball bearing. Shock. Vib. 2019, 1–12 (2019)

    Google Scholar 

  33. Li, B.Q., Ma, H., Yu, X., Zeng, J., Guo, X.M., Wen, B.C.: Nonlinear vibration and dynamic stability analysis of rotor-blade system with nonlinear supports. Arch. Appl. Mech. 89(7), 1375–1402 (2019)

    Article  Google Scholar 

  34. Liu, Y., Xin, X.C., Zhao, Y.L., Ming, S.S., Ma, Y.X., Han, J.Y.: Study on coupling fault dynamics of sliding bearing-rotor system. J. Comput. Nonlinear Dyn. 14(4), 041005 (2019)

    Article  Google Scholar 

  35. Chen, G., Qu, M.J.: Modeling and analysis of fit clearance between rolling bearing outer ring and housing. J. Sound Vib. 438, 419–440 (2019)

    Article  Google Scholar 

  36. Chen, G.: Study on nonlinear dynamic response of an unbalanced rotor supported on ball bearing. J. Vib. Acoust. 131(6), 061001 (2009)

    Article  Google Scholar 

  37. Zhang, W., Han, B.B., Li, X., Sun, J.Q., Ding, Q.: Multiple-objective design optimization of squirrel cage for squeeze film damper by using cell mapping method and experimental validation. Mech. Mach. Theory. 132, 66–79 (2019)

    Article  Google Scholar 

  38. Wang, D., Zhang, W.H., Wang, Z.P., Zhu, J.H.: Shape optimization of 3D curved slots and its application to the squirrel-cage elastic support design. Science China. Physics, Mechanics and Astronomy. 53(10), 1895–1900 (2010)

  39. Mao, Y.Z., Wang, L.Q., Zhang, C.W.: Study on the load distribution and dynamic characteristics of a thin-walled integrated squirrel-cage supporting roller bearing. Appl. Sci. 6(12), 415 (2016)

    Article  Google Scholar 

  40. Jin, Y.L., Lu, K., Huang, C.X., Hou, L., Chen, Y.S.: Nonlinear dynamic analysis of a complex dual rotor-bearing system based on a novel model reduction method. Appl. Math. Model. 75, 553–571 (2019)

    Article  MathSciNet  Google Scholar 

  41. Defaye, C., Nelias, D., Leblanc, A., Bon, F.: Theoretical analysis of high-speed cylindrical roller bearing with flexible rings mounted in a squeeze film damper. Tribol. Trans. 51(6), 762–770 (2008)

    Article  Google Scholar 

  42. Qin, W.Y., Zhang, J.F., Ren, X.M.: Response and bifurcation of rotor with squeeze film damper on elastic support. Chaos, Solitons Fractals 39(1), 188–195 (2009)

    Article  Google Scholar 

  43. Inayat-Hussain, J.I.: Bifurcations in the response of a flexible rotor in squeeze-film dampers with retainer springs. Chaos, Solitons Fractals 39(2), 519–532 (2009)

    Article  Google Scholar 

Download references

Funding

This work was supported by the National Natural Science Foundation of China [Grant Numbers 11872148, U1908217]; The Basic and Applied Basic Research Fund of Guangdong Province [Grant Numbers 2020B1515120015].

Author information

Authors and Affiliations

  1. School of Mechanical Engineering and Automation, Northeastern University, Shenyang, 110819, People’s Republic of China

    Kai Sun, Zhong Luo, Lei Li & Jiaxi Liu

  2. Key Laboratory of Vibration and Control of Aero-Propulsion Systems Ministry of Education of China, Northeastern University, Shenyang, 110819, People’s Republic of China

    Kai Sun, Zhong Luo, Lei Li & Jiaxi Liu

  3. Foshan Graduate School, Northeastern University, Foshan, 528312, People’s Republic of China

    Zhong Luo

  4. AECC Shenyang Engine Research Institute, Shenyang, 110015, People’s Republic of China

    Fayong Wu

Authors
  1. Kai Sun
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Zhong Luo
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Lei Li
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Jiaxi Liu
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Fayong Wu
    View author publications

    You can also search for this author in PubMed Google Scholar

Contributions

KS investigated the article, summarized the concepts and methods, wrote the original draft, and verified it with the corresponding software. ZL wrote, reviewed, and edited the article, and provided supervision and analysis. LL carried out software verification and visualization of the article, and managed the data. JL carried out software verification and visualization of the article. FW carried out software verification and visualization of the article.

Corresponding author

Correspondence to Zhong Luo.

Ethics declarations

Conflict of interest

The authors declare that they have no conflict of interest.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Sun, K., Luo, Z., Li, L. et al. Dynamic analysis of the variable stiffness support rotor system with elastic rings. Nonlinear Dyn 110, 201–217 (2022). https://doi.org/10.1007/s11071-022-07621-1

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11071-022-07621-1

Keywords

Search

Navigation