Forced sliding mode control for chaotic systems synchronization

Abstract

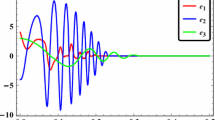
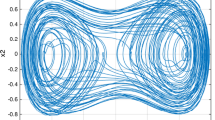
Synchronization of chaotic systems is considered to be a common engineering problem. However, the proposed laws of synchronization control do not always provide robustness toward the parametric perturbations. The purpose of this article is to show the use of synergy-cybernetic approach for the construction of robust law for Arneodo chaotic systems synchronization. As the main method of design of robust control, the method of design of control with forced sliding mode of the synergetic control theory is considered. To illustrate the effectiveness of the proposed law, in this article it is compared with the classical sliding mode control and adaptive backstepping. The distinctive features of suggested robust control law are the more good compensation of parametric perturbations (better performance indexes—the root-mean-square error (RMSE), average absolute value (AVG) of error) without designing perturbation observers, the ability to exclude the chattering effect, less energy consuming and a simpler analysis of the stability of a closed-loop system. The study of the proposed control law and the change of its parameters and the place of parametric perturbation’s application is carried out. It is possible to significantly reduce the synchronization error and RMSE, as well as AVG of error by reducing some parameters, but that leads to an increase in control signal amplitude. The place of application of parametric disturbances (slave or master system) has no effect on the RMSE and AVG of error. Offered approach will allow a new consideration for the design of robust control laws for chaotic systems, taking into account the ideas of directed self-organization and robust control. It can be used for synchronization other chaotic systems.

Appendices

Appendix A

The basic method of the SCT is the method of analytical designing aggregated regulators [28, 29]. Let us consider its stages described in [30].

Suppose the system to be controlled is described by a set of nonlinear differential equations in the form

$$\begin{aligned} \dot{x}(t) = f(x,u,t), \end{aligned}$$

(A.1)

where x is the state vector, u is the control input vector and t is time.

Let us start by defining a macro-variable as a function of the state variables:

$$\begin{aligned} \psi = \psi (x). \end{aligned}$$

(A.2)

The control will force the system to operate on the manifold $\psi =0$. The designer can select the characteristics of this macro-variable according to the control specifications (e.g., limitation of the control output, etc.). In a trivial case, the macro-variable can be a simple linear combination of the state variables. In a nontrivial case, it is complex nonlinear function.

The same process can be repeated, defining as many macro-variables as there are control channels.

The desired dynamic evolution of the macro-variable is

$$\begin{aligned} T \dot{\psi }(t) + \psi (x)=0, \quad T>0, \end{aligned}$$

(A.3)

where T is the design parameter specifying the convergence speed to the manifold specified by the macro-variable. The chain rule of differentiation (A.2) gives

$$\begin{aligned} \dot{\psi } = \frac{\text {d}\, \psi }{\text {d} \,x}\dot{x}(t) = \frac{\text {d}\, \psi }{\text {d} \,x} f(x,u,t). \end{aligned}$$

(A.4)

Combining (A.1), (A.3), and (A.4), we obtain

$$\begin{aligned} T \frac{\text {d}\, \psi }{\text {d} \,x} f(x,u,t) + \psi (x)=0. \end{aligned}$$

(A.5)

The Eq. (A.5) is finally used to synthesize the control law u : we express it from this equation.

To summarize, each manifold introduces a new constraint on the state space domain and reduces the order of the system, improving the global stability.

The procedure summarized here can be easily implemented as a computer program for automatic synthesis of the control law.

Appendix B

Let us introduce derivative for module function:

$$\begin{aligned} \dot{|x|} = \frac{\text {d}|x|}{\text {d}t}=\dot{x}(t){\text {sign}}(x). \end{aligned}$$

(B.6)

According (B.6), we find derivative of $\psi _1$ (5):

$$\begin{aligned} \dot{\psi }_1 (t)= \sum \limits _{j=1}^{n-1}\beta _{1j} {\text {sign}}(x_j)\dot{x}_j(t) + \dot{s}_1{\text {sign}}(s_1), \end{aligned}$$

(B.7)

and derivative of $s_1$ (6):

$$\begin{aligned} \dot{s}_1= \sum \limits _{j=1}^{n-1}\alpha _{1j} \dot{x}_j(t) + \dot{x}_n(t) + \sum \limits _{j=1}^{n-1}\frac{\partial u_1}{\partial x_j} \dot{x}_j(t). \end{aligned}$$

(B.8)

And now we can substitute (B.7) and (B.8) into (8) for $k=1$:

$$\begin{aligned} \begin{aligned}&T_1 \Biggl ( \sum \limits _{j=1}^{n-1}\beta _{1j} {\text {sign}}(x_j)\dot{x}_j(t) + \Bigl [ \sum \limits _{j=1}^{n-1}\alpha _{1j} \dot{x}_j(t) + \dot{x}_n(t) \\&+ \sum \limits _{j=1}^{n-1}\frac{\partial u_1}{\partial x_j} \dot{x}_j(t) \Bigr ] {\text {sign}}(s_1) \Biggr ) + \psi _1=0. \end{aligned} \end{aligned}$$

To simplify, we divide left part by $T_1$ and multiply by ${\text {sign}}(s_1)$:

$$\begin{aligned} \begin{aligned}&{\text {sign}}(s_1) \sum \limits _{j=1}^{n-1}\beta _{1j} {\text {sign}}(x_j)\dot{x}_j(t) + \sum \limits _{j=1}^{n-1}\alpha _{1j} \dot{x}_j(t) + \dot{x}_n(t) \\&+ \sum \limits _{j=1}^{n-1}\frac{\partial u_1}{\partial x_j} \dot{x}_j(t) + \frac{1}{T_1}\psi _1 {\text {sign}}(s_1) =0. \end{aligned} \end{aligned}$$

(B.9)

We substitute $\dot{x}_j(t)$ and $\dot{x}_n(t)$ from (4) in (B.9)

$$\begin{aligned} \begin{aligned}&{\text {sign}}(s_1) \sum \limits _{j=1}^{n-1}\beta _{1j} {\text {sign}}(x_j) \Bigl ( {{f}_{j}}\left( {{x}_{1}},\ldots ,{{x}_{n}} \right) +{{d}_{j+1}}{{x}_{j+1}}\Bigr ) \\&+ \sum \limits _{j=1}^{n-1}\alpha _{1j} \Bigl ( {{f}_{j}}\left( {{x}_{1}},\ldots ,{{x}_{n}} \right) +{{d}_{j+1}}{{x}_{j+1}}\Bigr ) + {{f}_{n}}\left( {{x}_{1}},\ldots ,{{x}_{n}} \right) \\&+u + \sum \limits _{j=1}^{n-1}\frac{\partial u_1}{\partial x_j} \dot{x}_j(t) + \frac{1}{T_1}\psi _1 {\text {sign}}(s_1) =0. \end{aligned} \end{aligned}$$

(B.10)

As a result, from (B.10) we can get the expression (9).