An avian influenza model with nonlinear incidence and recovery rates in deterministic and stochastic environments

Abstract

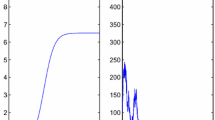
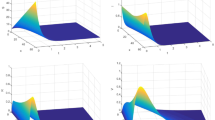
To assess the comprehensive impact of intervention strategies and available hospital resources, in this paper we first propose an avian influenza model with nonlinear incidence and recovery rates and investigate the local and global stability of the feasible equilibria. Taking into account the inherent randomness of the growth and spread of epidemics, we then extend the model into a random scenario and study the persistence, extinction and the existence of ergodic stationary distribution of the stochastic model. Finally, we numerically illustrate the obtained results. Both theoretical and numerical results show that: (i) Whether the avian influenza disappears or not depends entirely on the threshold in deterministic or random environment; (ii) Adequate hospital resources, government interventions and noise may suppress the outbreak of avian influenza virus; and (iii) Using multiple control strategies simultaneously is more effective in reducing the number of infections than using a single strategy.

Appendices

Appendix A

Proof

In fact, it follows from (4) that

(i):

If $e_1\le 0$, then there is only one sign change in the coefficients of f(x). By Descartes’ Rule of Signs [45], $f(x)=0$ has a unique positive root;

(ii):

If $e_1>0$, then

$$\begin{aligned}&f'(x)=4e_4x^3+3e_3x^2+2e_2x+e_1,\\&f(0)=e_0>0,\ f(+\infty )=-\infty . \end{aligned}$$

Clearly, there is only one sign change in the coefficients of $f'(x)$. Similarly, Descartes’ Rule of Signs [45] implies that $f'(x)=0$ has a unique positive root denoted by $x_+$. This, together with $f'(0)=e_1>0$ and $f'(+\infty )=-\infty$, yields that

$$\begin{aligned} {\left\{ \begin{array}{ll} 0<f'(x)\le e_1,\ 0\le x<x_+,\\ f'(x)\le 0,\ x\ge x_+. \end{array}\right. } \end{aligned}$$

Thus, f(x) is increasing for $0\le x<x_+$ and is decreasing for $x\ge x_+$, showing that Eq. (4) has a unique positive root. $\square$

Appendix B

Proof

Assume that $\epsilon$ meets the following conditions:

$$\begin{aligned}&-\frac{r_a}{2K_a}\frac{1}{{\epsilon }^3}+\varPhi _1\le -1, \end{aligned}$$

(B.1)

$$\begin{aligned}&-\frac{1}{2}(\mu _a+\delta _a-\frac{\sigma _2^2}{2})\frac{1}{\epsilon ^2}+\varPhi _2\le -1, \end{aligned}$$

(B.2)

$$\begin{aligned}&-\frac{1}{2}(\mu _h-\frac{\sigma _3^2}{2})\frac{1}{\epsilon ^2}+\varPhi _3\le -1, \end{aligned}$$

(B.3)

$$\begin{aligned}&-\frac{1}{2}(\mu _h+\delta _h-\frac{\sigma _4^2}{2})\frac{1}{\epsilon ^2}+\varPhi _4\le -1, \end{aligned}$$

(B.4)

$$\begin{aligned}&-\frac{1}{2}(\mu _h-\frac{\sigma _5^2}{2})\frac{1}{\epsilon ^2}+\varPhi _5\le -1, \end{aligned}$$

(B.5)

$$\begin{aligned}&0<\epsilon \le \frac{1}{M}, \end{aligned}$$

(B.6)

$$\begin{aligned}&-M(\mu _a+\delta _a+\frac{1}{2}\sigma _2^2)({\mathcal {R}}_0^S-1)\nonumber \\&\quad -\frac{\varPi _h}{\epsilon }+\varUpsilon \le -1, \end{aligned}$$

(B.7)

$$\begin{aligned}&-M(\mu _a+\delta _a+\frac{1}{2}\sigma _2^2)({\mathcal {R}}_0^S-1)\nonumber \\&\quad -\frac{\beta _h}{\epsilon (1+c\epsilon ^2)}+\varUpsilon \le -1, \end{aligned}$$

(B.8)

$$\begin{aligned}&-M(\mu _a+\delta _a+\frac{1}{2}\sigma _2^2)({\mathcal {R}}_0^S-1)\nonumber \\&\quad -\frac{\mu _0}{\epsilon }+\varUpsilon \le -1, \end{aligned}$$

(B.9)

where $\varPhi _i$ $(i=1, \ldots , 5)$, $\varUpsilon$ are defined as (B.10)-(B.15). For convenience, we then divide ${\mathbb {R}}_+^5\backslash U_{\epsilon }$ into ${\mathbb {R}}_+^5\backslash U_{\epsilon }=\bigcup _{k= 1}^{10}U_{\epsilon }^k$, where

$$\begin{aligned}&U_{\epsilon }^1=\{S_a>\frac{1}{\epsilon }\}, U_{\epsilon }^2=\{ I_a>\frac{1}{\epsilon }\}, U_{\epsilon }^3\\&\quad =\{ S_h>\frac{1}{\epsilon }\}, U_{\epsilon }^4=\{ I_h>\frac{1}{\epsilon }\},\\&U_{\epsilon }^{5}=\{ R_h>\frac{1}{\epsilon }\}, U_{\epsilon }^6=\{ 0<S_a<\epsilon \}, U_{\epsilon }^7\\&\quad =\{ 0<I_a<\epsilon \}, U_{\epsilon }^8=\{ 0<S_h<\epsilon \},\\&U_{\epsilon }^9=\{ 0<I_h<\epsilon ^3,I_a>\epsilon , S_h>\epsilon \}, U_{\epsilon }^{10}\\&\quad =\{ 0<R_h<\epsilon ^4, I_h>\epsilon ^3\}. \end{aligned}$$

We just need to prove ${\mathcal {L}}V_4\le -1$ in each $U_{\epsilon }^k,\ k=1, \cdots , 10$, which means in ${\mathbb {R}}_+^5\backslash U_{\epsilon }$.

Case 1::

If $X(t)\in U_{\epsilon }^1$, by (24) and (B.1), then

$$\begin{aligned} {\mathcal {L}}V_{4}\le&M\beta _a(b+m_2)(\frac{3}{7}S_a^{\frac{7}{3}}+\frac{4}{7}I_a^{\frac{7}{4}})+\sum \limits _{i=1}^5H_i\\ \le&-\frac{r_a}{2K_a}\frac{1}{{\epsilon }^3}+\varPhi _1\le -1, \end{aligned}$$

where

$$\begin{aligned}&\varPhi _1=\sup \limits _{X(t)\in {\mathbb {R}}_+^5}\{M\beta _a(b+m_2)(\frac{3}{7}S_a^{\frac{7}{3}} +\frac{4}{7}I_a^{\frac{7}{4}})\nonumber \\&\quad +\frac{r_a}{2K_a}S_a^3+\sum \limits _{i=1}^5H_i\}<\infty . \end{aligned}$$

(B.10)

If $X(t)\in U_{\epsilon }^2$, then it follows from (24) and (B.2) that

$$\begin{aligned} \mathcal {L}V_{4}\le -\frac{1}{2}(\mu _a+\delta _a-\frac{\sigma _2^2}{2})\frac{1}{\epsilon ^2}+\varPhi _2\le -1, \end{aligned}$$

where

$$\begin{aligned}&\varPhi _2=\sup \limits _{X(t)\in {\mathbb {R}}_+^5}\{M\beta _a(b+m_2)(\frac{3}{7}S_a^{\frac{7}{3}} +\frac{4}{7}I_a^{\frac{7}{4}})\nonumber \\&\quad +\frac{1}{2}(\mu _a+\delta _a-\frac{\sigma _2^2}{2})I_a^2+\sum \limits _{i=1}^5H_i\}<\infty . \end{aligned}$$

(B.11)

If $X(t)\in U_{\epsilon }^3$, then (24) and (B.3) imply that

$$\begin{aligned} \mathcal {L}V_{4}\le -\frac{1}{2}(\mu _h-\frac{\sigma _3^2}{2})\frac{1}{\epsilon ^2}+\varPhi _3\le -1, \end{aligned}$$

where

$$\begin{aligned}&\varPhi _3=\sup \limits _{X(t)\in {\mathbb {R}}_+^5}\{M\beta _a(b+m_2)(\frac{3}{7}S_a^{\frac{7}{3}} +\frac{4}{7}I_a^{\frac{7}{4}})\nonumber \\&\quad +\frac{1}{2}(\mu _h-\frac{\sigma _3^2}{2})S_h^2+\sum \limits _{i=1}^5H_i\}<\infty . \end{aligned}$$

(B.12)

If $X(t)\in U_{\epsilon }^4$, then it can be seen from (24) and (B.4) that

$$\begin{aligned} \mathcal {L}V_{4}\le -\frac{1}{2}(\mu _h+\delta _h-\frac{\sigma _4^2}{2})\frac{1}{\epsilon ^2}+\varPhi _4\le -1, \end{aligned}$$

where

$$\begin{aligned}&\varPhi _4=\sup \limits _{X(t)\in {\mathbb {R}}_+^5}\{M\beta _a(b+m_2)(\frac{3}{7}S_a^{\frac{7}{3}} +\frac{4}{7}I_a^{\frac{7}{4}})\nonumber \\&\quad +\frac{1}{2}(\mu _h+\delta _h-\frac{\sigma _4^2}{2})I_h^2+\sum \limits _{i=1}^5H_i\}<\infty . \end{aligned}$$

(B.13)

If $X(t)\in U_{\epsilon }^5$, by (24) and (B.5), then

$$\begin{aligned} \mathcal {L}V_{4}\le -\frac{1}{2}(\mu _h-\frac{\sigma _5^2}{2})\frac{1}{\epsilon ^2}+\varPhi _5\le -1, \end{aligned}$$

where

$$\begin{aligned}&\varPhi _5=\sup \limits _{X(t)\in {\mathbb {R}}_+^5}\{M\beta _a(b+m_2)(\frac{3}{7}S_a^{\frac{7}{3}} +\frac{4}{7}I_a^{\frac{7}{4}})\nonumber \\&\quad +\frac{1}{2}(\mu _h-\frac{\sigma _5^2}{2})R_h^2+\sum \limits _{i=1}^5H_i\}<\infty . \end{aligned}$$

(B.14)

Case 2::

If $X(t)\in U_{\epsilon }^6$, using (24), (B.6) and the definitions of M and $\phi _1$, then

$$\begin{aligned} {\mathcal {L}}V_{4}&\le -M(\mu _a+\delta _a+\frac{1}{2}\sigma _2^2)({\mathcal {R}}_0^S-1)\\&\quad -\beta _a(b+m_2)(1-M\epsilon )I_a\\&+\beta _a(b+m_2)I_a+\sum \limits _{i=1}^5H_i\\&\le -M(\mu _a+\delta _a+\frac{1}{2}\sigma _2^2)({\mathcal {R}}_0^S-1)\\&\quad -\beta _a(b+m_2)(1-M\epsilon )I_a+\phi _1\\&\le -\frac{1}{2}M(\mu _a+\delta _a+\frac{1}{2}\sigma _2^2)({\mathcal {R}}_0^S-1)\le -1. \end{aligned}$$

Similarly, if $X(t)\in U_{\epsilon }^7$, then we also have

$$\begin{aligned} {\mathcal {L}}V_{4}&\le -M(\mu _a+\delta _a+\frac{1}{2}\sigma _2^2)({\mathcal {R}}_0^S-1)\\&\quad -\beta _a(b+m_2)(1-M\epsilon )S_a+\phi _2\\&\le -\frac{1}{2}M(\mu _a+\delta _a+\frac{1}{2}\sigma _2^2)({\mathcal {R}}_0^S-1)\le -1. \end{aligned}$$

Case 3::

If $X(t)\in U_{\epsilon }^8$, using (24) and (B.7), then

$$\begin{aligned} {\mathcal {L}}V_{4} \le&-M(\mu _a+\delta _a+\frac{1}{2}\sigma _2^2)({\mathcal {R}}_0^S-1)\\&\quad -\frac{\varPi _h}{\epsilon }+\varUpsilon \le -1, \end{aligned}$$

where

$$\begin{aligned} \varUpsilon= & {} \sup \limits _{X(t)\in {\mathbb {R}}_+^5}\{M\beta _a(b+m_2)S_aI_a\nonumber \\&+\sum \limits _{i=1}^5H_i\}<\infty . \end{aligned}$$

(B.15)

If $X(t)\in U_{\epsilon }^9$, applying (24) and (B.8), then

$$\begin{aligned}&{\mathcal {L}}V_{4}\le -M(\mu _a+\delta _a+\frac{1}{2}\sigma _2^2)({\mathcal {R}}_0^S-1)\\&\quad -\frac{\beta _h}{\epsilon (1+c\epsilon ^2)}+\varUpsilon \le -1. \end{aligned}$$

If $X(t)\in U_{\epsilon }^{10}$, by (24) and (B.9), then

$$\begin{aligned} \mathcal {L}V_{4}&\le -M(\mu _a+\delta _a+\frac{1}{2}\sigma _2^2)({\mathcal {R}}_0^S-1)\\&\quad -\frac{\mu _0}{\epsilon }+\varUpsilon \le -1. \end{aligned}$$

In short, we have ${\mathcal {L}}V_4\le -1$ on ${\mathbb {R}}_+^5\backslash U_{\epsilon }$. $\square$