Skip to main content
SpringerLink
Log in

Learning high-order geometric flow based on the level set method

  • Original Paper
  • Published:
Nonlinear Dynamics Aims and scope Submit manuscript

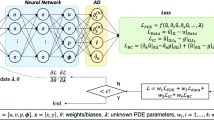
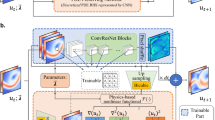
Abstract

Recently, the development of deep learning has accomplished unbelievable success in many fields, especially in scientific computational fields. And almost all computational problems and physical phenomena can be described by partial differential equations. In this work, we proposed two potential high-order geometric flows. Motivation by the physical-information neural networks and the traditional level set method (LSM), we have integrated deep neural networks and LSM to make the proposed method more robust and efficient. Also, to test the sensitivity of the system to different input data, we set up three sets of initial conditions to test the model. Furthermore, numerical experiments on different input data are implemented to demonstrate the effectiveness and superiority of the proposed models compared to the state-of-the-art approach.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5

Similar content being viewed by others

References

  1. Bachmann, G., Bécigneul, G., Ganea, O.-E.: Constant curvature graph convolutional networks. In: International Conference on Machine Learning (2020)

  2. Long, Z., Lu, Y., Ma, X., Dong, B.: PDE-net: learning PDEs from data. In: International Conference on Machine Learning, pp. 3208–3216, PMLR (2018)

  3. Sanchez-Gonzalez, A., Godwin, J., Pfaff, T., Ying, R., Leskovec, J., Battaglia, P.: Learning to simulate complex physics with graph networks. In: International Conference on Machine Learning, pp. 8459–8468, PMLR (2020)

  4. Xue, T., Beatson, A., Adriaenssens, S., Adams, R.: Amortized finite element analysis for fast PDE-constrained optimization. In: International Conference on Machine Learning, pp. 10638–10647. PMLR (2020)

  5. Li, C., Yang, Y., Liang, H., Wu, B.: Robust PCL discovery of data-driven mean-field game systems and control problems. In: IEEE Transactions on Circuits and Systems I-Regular Papers, pp. 1–14 (2021)

  6. Li, C., Yang, Y., Liang, H., Wu, B.: Transfer learning for establishment of recognition of COVID-19 on CT imaging using small-sized training datasets. Knowl. Based Syst. 218, 106849–106849 (2021)

    Article  Google Scholar 

  7. Bretin, E., Masnou, S., Sengers, A., Terii, G.: Approximation of surface diffusion flow: a second order variational Cahn–Hilliard model with degenerate mobilities. arXiv:2007.03793 (2020)

  8. Dang, W., ke Gao, Z., Hou, L., Lv, D., Qiu, S., Chen, G.: A novel deep learning framework for industrial multiphase flow characterization. In: IEEE Transactions on Industrial Informatics, vol. 15, pp. 5954–5962 (2019)

  9. Gao, Z., Dang, W., Mu, C., Yang, Y., Li, S., Grebogi, C.: A novel multiplex network-based sensor information fusion model and its application to industrial multiphase flow system. IEEE Trans. Industr. Inf. 14, 3982–3988 (2018)

    Article  Google Scholar 

  10. Liang, L., Jin, L., Xu, Y.: PDE learning of filtering and propagation for task-aware facial intrinsic image analysis. IEEE Trans. Cybern. 55, 1–14 (2020)

    Google Scholar 

  11. Chen, D., Zhu, J., Zhang, X., Shu, M., Cohen, L.D.: Geodesic paths for image segmentation with implicit region-based homogeneity enhancement. IEEE Trans. Image Process. 30, 5138–5153 (2021)

    Article  MathSciNet  Google Scholar 

  12. Chen, J., Amini, A.A.: Quantifying 3-D vascular structures in MRA Images Using Hybrid PDE and geometric deformable models. IEEE Trans. Med. Imaging 23(10), 1251–1262 (2004)

    Article  Google Scholar 

  13. Salinas, H.M., Fernández, D.C.: Comparison of PDE-based nonlinear diffusion approaches for image enhancement and denoising in optical coherence tomography. IEEE Trans. Med. Imaging 26(6), 761–771 (2007)

    Article  Google Scholar 

  14. Karasev, P., Kolesov, I., Fritscher, K., Vela, P., Mitchell, P., Tannenbaum, A.: Interactive medical image segmentation using PDE control of active contours. IEEE Trans. Med. Imaging 32(11), 2127–2139 (2013)

    Article  Google Scholar 

  15. Biroon, R.A., Biron, Z.A., Pisu, P.: False data injection attack in a platoon of CACC: real-time detection and isolation with a PDE approach. IEEE Trans. Intell. Transp. Syst. 22, 1–12 (2021)

    Google Scholar 

  16. Deutscher, J.: Robust cooperative output regulation for a network of parabolic PDE systems. IEEE Trans. Autom. Control 66, 1 (2021)

    Google Scholar 

  17. Song, X., Zhang, Q., Zhang, Y., Song, S.: Fuzzy event-triggered control for pde systems with pointwise measurements based on relaxed Lyapunov-Krasovskii functionals. IEEE Trans. Fuzzy Syst. 29, 1 (2021)

    Google Scholar 

  18. Zhao, D., Jiang, B., Yang, H.: Backstepping-based decentralized fault-tolerant control of hypersonic vehicles in PDE-ODE form. IEEE Trans. Autom. Control 66, 1–1 (2021)

    Google Scholar 

  19. Oliveira, T.R., Feiling, J., Koga, S., Krstić, M.: Multivariable extremum seeking for PDE dynamic systems. IEEE Trans. Autom. Control 65(11), 4949–4956 (2020)

    Article  MathSciNet  MATH  Google Scholar 

  20. Osher, S., Sethian, J.A.: Fronts propagating with curvature-dependent speed: algorithms based on Hamilton–Jacobi formulations. J. Comput. Phys. 79(1), 12–49 (1988)

    Article  MathSciNet  MATH  Google Scholar 

  21. Raissi, M., Karniadakis, G.E.: Hidden physics models: machine learning of nonlinear partial differential equations. J. Comput. Phys. 357, 125–141 (2018)

    Article  MathSciNet  MATH  Google Scholar 

  22. Raissi, M., Perdikaris, P., Karniadakis, G.E.: Physics-informed neural networks: a deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations. J. Comput. Phys. 378, 686–707 (2019)

    Article  MathSciNet  MATH  Google Scholar 

  23. Guoliang, X., Qin, Z.: Construction of geometric partial differential equations in computational geometry. Math. Numer. Sin. Chin. Ed. 28(4), 337 (2006)

    MathSciNet  Google Scholar 

  24. Lustig, E., Yair, O., Talmon, R., Segev, M.: Identifying topological phase transitions in experiments using manifold learning. Phys. Rev. Lett. 125(12), 127401 (2020)

    Article  Google Scholar 

  25. Eo, T., Shin, H., Jun, Y., Kim, T., Hwang, D.: Accelerating Cartesian MRI by domain-transform manifold learning in phase-encoding direction. Med. Image Anal. 63, 101689 (2020)

    Article  Google Scholar 

  26. Ma, Z., Zhan, Z., Feng, Z., Guo, J.: Manifold learning based on straight-like geodesics and local coordinates. IEEE Trans. Neural Netw. Learn. Syst. 31, 4965–4970 (2020)

    Google Scholar 

  27. Pournemat, A., Adibi, P., Chanussot, J.: Semisupervised charting for spectral multimodal manifold learning and alignment. Pattern Recogn. 111, 107645 (2021)

    Article  Google Scholar 

  28. Mehrdad, S., Kahaei, M.H.: Deep learning approach for matrix completion using manifold learning. Signal Process. 188, 108231 (2021)

    Article  Google Scholar 

  29. Rodrigues, C.M., Soriano-Vargas, A., Lavi, B., Rocha, A., Dias, Z.: Manifold learning for real-world event understanding. IEEE Trans. Inf. Forensics Secur. 16, 2957–2972 (2021)

    Article  Google Scholar 

  30. Chen, X., Chen, R., Wu, Q., Nie, F., Yang, M., Mao, R.: Semisupervised feature selection via structured manifold learning. IEEE Trans. Cybern. 51, 1–11 (2021)

    Google Scholar 

  31. Yan, S., Tai, X., Liu, J., Huang, H.: Convexity shape prior for level set-based image segmentation method. IEEE Trans. Image Process. 29, 7141–7152 (2020)

    Article  MathSciNet  Google Scholar 

  32. Falcone, M., Paolucci, G., Tozza, S.: A high-order scheme for image segmentation via a modified level-set method. SIAM J. Imag. Sci. 13, 497–534 (2020)

    Article  MathSciNet  MATH  Google Scholar 

  33. Liu, D., Gu, D., Smyl, D., Deng, J., Du, J.: B-spline level set method for shape reconstruction in electrical impedance tomography. IEEE Trans. Med. Imaging 39, 1917–1929 (2020)

    Article  Google Scholar 

  34. Howard, A.A., Tartakovsky, A.: A conservative level set method for N-phase flows with a free-energy-based surface tension model. J. Comput. Phys. 426, 109955 (2021)

    Article  MathSciNet  Google Scholar 

  35. Larios-Cárdenas, L.Á., Gibou, F.: A deep learning approach for the computation of curvature in the level-set method. J. Comput. Phys. 43, A1754–A1779 (2021)

    MathSciNet  MATH  Google Scholar 

  36. He, W., Song, H., Yao, Y., Jia, X., Long, Y.: A novel level set method for inhomogeneous SAR image segmentation. IEEE Geosci. Remote Sens. Lett. 18, 1044–1048 (2021)

    Article  Google Scholar 

  37. Huang, J., Wang, H., Yang, H.: Int-deep: a deep learning initialized iterative method for nonlinear problems. J. Comput. Phys. 419, 109675 (2020)

    Article  MathSciNet  Google Scholar 

  38. Belbute-Peres, F. d. A., Economon, T., Kolter, Z.: Combining differentiable PDE solvers and graph neural networks for fluid flow prediction. In: International Conference on Machine Learning, pp. 2402–2411. PMLR (2020)

  39. So, C.C., Li, T.O., Wu, C., Yung, S.P.: Differential spectral normalization (DSN) for PDE discovery. Proc. AAAI Conf. Artif. Intell. 35, 9675–9684 (2021)

    Google Scholar 

  40. Bar, L., Sochen, N.: Strong solutions for PDE-based tomography by unsupervised learning. SIAM J. Imag. Sci. 14, 128–155 (2021)

    Article  MathSciNet  MATH  Google Scholar 

  41. Lu, L., Jin, P., Pang, G., Zhang, Z., Karniadakis, G.E.: Learning nonlinear operators via DeepONet based on the universal approximation theorem of operators. Nat Mach Intell 3(3), 218–229 (2021)

    Article  Google Scholar 

  42. Thanasutives, P., Fukui, K.-i., Numao, M.: Adversarial multi-task learning enhanced physics-informed neural networks for solving partial differential equations. arXiv:2104.14320 (2021)

  43. Chen, D., Jacob, L., Mairal, J.: Convolutional kernel networks for graph-structured data. In: International Conference on Machine Learning, pp. 1576–1586. PMLR (2020)

  44. Chowdhury, A.R., Rekatsinas, T., Jha, S.: Data-dependent differentially private parameter learning for directed graphical models. In: International Conference on Machine Learning, pp. 1939–1951. PMLR (2020)

  45. Sundaramoorthi, G., Yezzi, A.: Variational PDEs for acceleration on manifolds and application to diffeomorphisms. In: The Conference on Neural Information Processing Systems (2018)

  46. Zhu, W., Qiu, Q., Huang, J., Calderbank, R., Sapiro, G., Daubechies, I.: LDMNet: low dimensional manifold regularized neural networks. In: Proceedings of the IEEE conference on computer vision and pattern recognition, pp. 2743–2751 (2018)

  47. Bai, L., Shao, Y., Chen, W., Wang, Z., Deng, N.: Multiple flat projections for cross-manifold clustering. IEEE Trans Cybern 51, 1–15 (2021)

    Article  Google Scholar 

  48. Tan, C., Chen, S., Ji, G., Geng, X.: Multilabel distribution learning based on multioutput regression and manifold learning. IEEE Trans. Cybern 50, 1–15 (2020)

    Google Scholar 

  49. Sethian, J.A.: Level Set Methods and Fast Marching Methods: Evolving Interfaces in Computational Geometry, Fluid Mechanics, Computer Vision, and Materials Science, vol. 3. Cambridge University Press, Cambridge (1999)

    MATH  Google Scholar 

  50. Fedkiw, S.O.R., Osher, S.: Level set methods and dynamic implicit surfaces. Surfaces 44, 77 (2002)

    MATH  Google Scholar 

  51. Lin, Q., Ma, R., Yang, T.: Level-set methods for finite-sum constrained convex optimization. In: International conference on machine learning, pp. 3112–3121. PMLR (2018)

  52. Li, C., Huang, R., Ding, Z., Gatenby, C., Metaxas, D.N., Gore, J.: A level set method for image segmentation in the presence of intensity inhomogeneities with application to MRI. IEEE Trans. Image Process. 20, 2007–2016 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  53. Brox, T., Weickert, J.: Level set segmentation with multiple regions. IEEE Trans. Image Process. 15, 3213–3218 (2006)

    Article  Google Scholar 

  54. Li, C., Xu, C., Gui, C., Fox, M.: Distance regularized level set evolution and its application to image segmentation. IEEE Trans. Image Process. 19, 3243–3254 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  55. Zhang, K., Zhang, L., Lam, K., Zhang, D.: A level set approach to image segmentation with intensity inhomogeneity. IEEE Trans. Cybern. 46, 546–557 (2016)

    Article  Google Scholar 

  56. Zuzio, D., Orazzo, A., Estivalezes, J., Lagrange, I.: A new efficient momentum preserving level-set/VOF method for high density and momentum ratio incompressible two-phase flows. J. Comput. Phys. 410, 109342 (2020)

    Article  MathSciNet  MATH  Google Scholar 

  57. Zhang, J., Yue, P.: A level-set method for moving contact lines with contact angle hysteresis. J. Comput. Phys. 418, 109636 (2020)

    Article  MathSciNet  Google Scholar 

  58. Dugast, F., Favennec, Y., Josset, C.: Reactive fluid flow topology optimization with the multi-relaxation time lattice boltzmann method and a level-set function. J. Comput. Phys. 409, 109252 (2020)

    Article  MathSciNet  MATH  Google Scholar 

  59. Theillard, M.: A volume-preserving reference map method for the level set representation. J. Comput. Phys. 442, 110478 (2021)

    Article  MathSciNet  Google Scholar 

  60. Xue, T., Sun, W., Adriaenssens, S., Wei, Y., Liu, C.: A new finite element level set reinitialization method based on the shifted boundary method. J. Comput. Phys. 438, 110360 (2021)

    Article  MathSciNet  Google Scholar 

  61. Zhang, F., Liu, T., Liu, M.: A high-order maximum-principle-satisfying discontinuous Galerkin method for the level set problem. J. Sci. Comput. 87, 45 (2021)

    Article  MathSciNet  MATH  Google Scholar 

  62. Sirignano, J.A., Spiliopoulos, K.: DGM: a deep learning algorithm for solving partial differential equations. J. Comput. Phys. 375, 1339–1364 (2018)

    Article  MathSciNet  MATH  Google Scholar 

  63. Chen, T.Q., Rubanova, Y., Bettencourt, J., Duvenaud, D.: Neural ordinary differential equations. In: The Conference on Neural Information Processing Systems (2018)

  64. Han, J., Jentzen, A.E.W.: Solving high-dimensional partial differential equations using deep learning. Proc. Natl. Acad. Sci. 115, 8505–8510 (2018)

    Article  MathSciNet  MATH  Google Scholar 

  65. Lu, L., Meng, X., Mao, Z., Karniadakis, G.E.: DeepXDE: a deep learning library for solving differential equations. SIAM Rev. 63(1), 208–228 (2021)

    Article  MathSciNet  MATH  Google Scholar 

  66. Cai, S., Wang, Z., Lu, L., Zaki, T.A., Karniadakis, G.E.: DeepM&Mnet: inferring the electroconvection multiphysics fields based on operator approximation by neural networks. J. Comput. Phys. 23, 110296 (2021)

    Article  MathSciNet  Google Scholar 

  67. Zhao, L., Li, Z., Wang, Z., Caswell, B., Ouyang, J., Karniadakis, G.E.: Active-and transfer-learning applied to microscale-macroscale coupling to simulate viscoelastic flows. J. Comput. Phys. 427, 110069 (2021)

    Article  MathSciNet  Google Scholar 

  68. Yang, L., Meng, X., Karniadakis, G.E.: B-PINNs: Bayesian physics-informed neural networks for forward and inverse PDE problems with noisy data. J. Comput. Phys. 425, 109913 (2021)

    Article  MathSciNet  Google Scholar 

  69. Aubert, G., Kornprobst, P.: Mathematical Problems in Image Processing: Partial Differential Equations and the Calculus of Variations, vol. 147. Springer, Berlin (2006)

    MATH  Google Scholar 

  70. Guo, S., Yan, Z., Zhang, K., Zuo, W., Zhang, L.: Toward convolutional blind denoising of real photographs . In: Proceedings of the IEEE/CVF conference on computer vision and pattern recognition, pp. 1712–1722 (2019)

  71. Zhang, Y., Tian, Y., Kong, Y., Zhong, B., Fu, Y.R.: Residual dense network for image super-resolution. In: 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, pp. 2472–2481 (2018)

  72. Yue, Z., Yong, H., Zhao, Q., Zhang, L.M., Meng, D.: Variational denoising network: toward blind noise modeling and removal. In: NeurIPS (2019)

  73. Zhang, K., Zuo, W., Chen, Y., Meng, D., Zhang, L.: Beyond a Gaussian denoiser: residual learning of deep CNN for image denoising. IEEE Trans. Image Process. 26(7), 3142–3155 (2017)

    Article  MathSciNet  MATH  Google Scholar 

  74. Bourlard, H., Wellekens, C.J.: Links between Markov models and multilayer perceptrons. IEEE Trans. Pattern Anal. Mach. Intell. 12(12), 1167–1178 (1990)

    Article  Google Scholar 

  75. Hore, A., Ziou, D.: Image quality metrics: PSNR vs. SSIM. In: 2010 20th International Conference on Pattern Recognition, pp. 2366–2369. IEEE (2010)

  76. Paszke, A., Gross, S., Massa, F., Lerer, A., Bradbury, J., Chanan, G., Killeen, T., Lin, Z., Gimelshein, N., Antiga, L., et al.: Pytorch: an imperative style, high-performance deep learning library. Adv. Neural. Inf. Process. Syst. 32, 8026–8037 (2019)

    Google Scholar 

  77. Zeiler, M.D.: Adadelta: an adaptive learning rate method. arXiv:1212.5701 (2012)

  78. Duchi, J., Hazan, E., Singer, Y.: Adaptive subgradient methods for online learning and stochastic optimization. J. Mach. Learn. Res. 12, 7 (2011)

    MathSciNet  MATH  Google Scholar 

  79. Kingma, D.P., Ba, J.: Adam: a method for stochastic optimization. arXiv:1412.6980 (2014)

  80. Graves, A.: Generating sequences with recurrent neural networks. arXiv:1308.0850 (2013)

Download references

Acknowledgements

Thank you for your valuable comments from any anonymous reviewers.

Funding

This Project is funded by China Postdoctoral Science Foundation (No. 2021M690837) and Shenzhen Higher Education Institutions Stable Support Plan (Nos. GXWD20201230155 427003-20200729105427008).

Author information

Authors and Affiliations

  1. School of Science, Harbin Institute of Technology, Shenzhen, 518055, China

    Chun Li, Yunyun Yang & Hui Liang

  2. School of Mathematics, Harbin Institute of Technology, Harbin, 150001, China

    Boying Wu

Authors
  1. Chun Li
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Yunyun Yang
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Hui Liang
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Boying Wu
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Yunyun Yang.

Ethics declarations

Conflict of interest

The authors declare that there is no conflict of interest regarding the publication of this paper.

Data Availability

All materials (data and code) are available from GitHub (https://github.com/lichun0503/learning-Geometric-Flow).

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Li, C., Yang, Y., Liang, H. et al. Learning high-order geometric flow based on the level set method. Nonlinear Dyn 107, 2429–2445 (2022). https://doi.org/10.1007/s11071-021-07043-5

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11071-021-07043-5

Keywords

Search

Navigation