Abstract
In this paper, we introduce a generalization of Lyapunov’s direct method for dynamical systems with fractional damping. Hereto, we embed such systems within the fundamental theory of functional differential equations with infinite delay and use the associated stability concept and known theorems regarding Lyapunov functionals including a generalized invariance principle. The formulation of Lyapunov functionals in the case of fractional damping is derived from a mechanical interpretation of the fractional derivative in infinite state representation. The method is applied on a single degree-of-freedom oscillator first, and the developed Lyapunov functionals are subsequently generalized for the finite-dimensional case. This opens the way to a stability analysis of nonlinear (controlled) systems with fractional damping. An important result of the paper is the solution of a tracking control problem with fractional and nonlinear damping. For this problem, the classical concepts of convergence and incremental stability are generalized to systems with fractional-order derivatives of state variables. The application of the related method is illustrated on a fractionally damped two degree-of-freedom oscillator with regularized Coulomb friction and non-collocated control.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Avoid common mistakes on your manuscript.
1 Introduction
Many problems in industrial applications originate from (dynamic) instability phenomena, e.g., stick-slip vibrations, flutter, shimmy of vehicles and feedback instabilities in control systems. Methods to rigorously prove stability of linear and nonlinear systems are quintessential for the mitigation of instability-induced vibration through improved design, vibration observers or feedback control. The Lyapunov stability framework, which encompasses the direct method of Lyapunov, forms a central element in the research fields Nonlinear Dynamics and Control Theory [17]. The Lyapunov approach is classically formulated for ordinary differential equations (ODEs). It is the aim of this paper to provide a generalization of the direct method of Lyapunov for ODEs that contain additional fractional derivatives of system states.
The term fractional refers to the mathematical theory of fractional calculus dealing with derivatives and integrals of arbitrary (non-integer) order, see, e.g., [6, 29, 33] for an introduction. The theory has proven to be applicable on a wide range of phenomena in various disciplines of science and engineering, see [12, 39] for an overview. Particularly in mechanics, it is used to model viscoelastic material behavior, which is characterized by long-term creep and relaxation processes. Herein, the introduction of a springpot element plays an essential role. It represents a force law reacting linearly on a fractional derivative of its elongation, behaving in-between a classical spring and a dashpot for a fractional order between zero and one. The use of springpot elements leads to good approximations in models with few parameters and much better extrapolation properties on large time and frequency scales in comparison with classical rheological models [2, 38].
The introduction of springpots in (controlled) nonlinear mechanical systems asks for an extension of the Lyapunov stability framework. A major complication arises through the non-local character of fractional derivatives, i.e., the force in a springpot element depends on the total history of the elongation. A system with springpot elements has therefore an infinite memory and has to be described by an infinite number of states which asks for the use of Lyapunov functionals instead of Lyapunov functions in Lyapunov’s direct method. Therefore, a finite-dimensional mechanical system with additional springpots has to be considered as a functional differential equation (FDE), for which a related Lyapunov theory exists [3, 4, 9, 19, 21].
A source of inspiration for the construction of Lyapunov functionals for mechanical systems is the total mechanical energy. For the case of a springpot, an interpretation as an infinite arrangement of springs and dashpots, see [13, 30, 37], leads to a potential energy term which was also derived in [11, 42, 43] for an electrical system. It leads to an energy Lyapunov functional with expressions based on the infinite state representation (also known as diffusive representation) of fractional integrators, which were introduced by Montseny [28], Matignon [26] and have been elaborated by Trigeassou et al. [42,43,44,45,46].
Beyond the results mentioned so far, a lot of work has been done on stability of fractional differential equations including Matignon’s spectral condition for linear systems [25], linear matrix inequalities [34] or fractional-order control [27]. Furthermore, some results regarding Lyapunov functions and special stability concepts exist [7, 20, 23]. However, they cannot be used for ODE systems containing springpots, as a (generally) irrational differentiation order leads to an incommensurate fractional system. Therefore, the energy Lyapunov functionals in infinite state representation combined with the theory of FDEs appear to be a promising approach to tackle the described problem and recently in [15], we used this idea to prove stability of a fractionally damped single degree-of-freedom oscillator with additional viscous (anti-)damping using several Lyapunov functionals.
In this paper, it is the aim to extend the method described in [15] in three different ways. First, we consider fractional derivatives with an infinite lower bound of integration, which leads (in contrast to [15]) to an interpretation of fractionally damped systems as autonomous FDEs with infinite delay and allows for the use of a generalized invariance principle which we develop in this paper. Furthermore, the approach for a single degree-of-freedom oscillator is generalized for finite-dimensional mechanical systems with fractional damping. Finally, the results are directly applied to solve a tracking control problem. The paper is organized as follows. We introduce the necessary content on fractional calculus (Sect. 2) and summarize the theory on FDEs and the related method of Lyapunov functionals (Sect. 3). Therein, the generalized invariance principle (Theorem 5) is proven. Furthermore, we adapt the results in [15] regarding Lyapunov functionals for a single degree-of-freedom oscillator in the autonomous case (Sects. 4.1–4.4) and deduce the generalization for finite-dimensional linear fractionally damped mechanical systems (Sect. 4.5). In a second step, the results are applied on a controlled fractionally damped dynamical system with Lur’e-type nonlinearity (Sect. 5). Particularly, we aim at tracking of a desired solution using feedback and feedforward control. The related stability criteria are based on generalizations of the classical concepts of convergent dynamics [31, 32] and incremental stability [1] and use an incremental Lyapunov functional inspired from the classical case and the functionals used in Sect. 4. Finally, we study the example of a two degree-of-freedom mechanical archetype system with regularized Coulomb friction and non-collocated control and prove tracking of a desired solution (Sect. 5.3).
2 Fractional calculus and springpots
2.1 Fractional derivatives and the infinite state representation
We consider the fractional Caputo derivative [5, 6] of order \(\alpha \in (0,1)\) of a continuously differentiable real-valued function q(t) as
with the Gamma function
The differential operator in (1) considers the entire history \((-\infty ,0]\) of the function q, and we think of \(t=0\) as initial time to start integration of a differential equation containing fractional derivatives, i.e., the complete history of q is an initial datum. The meaning and application of the fractional Caputo derivative are explained in the standard references [6, 33].
Remark 1
There is a broad discussion within the scientific community about the “correct” initial conditions for differential equations containing fractional derivatives. We choose an infinite lower bound for the integral in (1), as this leads to an autonomous FDE in Sect. 3. This choice is compatible to the notions in [24, 35, 41, 47].
Another description of (1) is the infinite state representation
with the infinite states \(z(\eta ,t)\) (denoted \(z_C(\eta ,t)\) in [46]), where
as introduced in [26, 28, 46]. To see the correspondence between (1) and (3), we use (4) and (2) to obtain
where we substituted \(u=\omega t\) and used the property
We obtain (3) by inserting (5) in (1), using Fubini’s theorem and the solution of the initial value problem in (3), namely
such that
The infinite state representation translates the fractional derivative to integer order at the cost of a continuum of state variables. Correspondingly, the history of the function q is transferred to initial conditions of the infinite states
Furthermore, we utilize a second kind of infinite states \(Z(\eta ,t)\) (denoted \(z_{RL} (\eta ,t)\) in [46] as it is associated with the fractional Riemann–Liouville derivative) characterized by
which will prove to be useful for the formulation of Lyapunov functionals later. The solution of (9) is given by
and it is related to the infinite states \(z(\eta ,t)\) in (3) by
whenever q is bounded.
2.2 Mechanical representation and potential energy of springpots
In mechanics, we consider fractional derivatives to model hereditary material behavior. In particular, a so-called springpot (Fig. 1), see [18], is considered as an abstract mechanical element which fulfills a force law of the form
where the elongation q of the springpot element changes according to (11) depending on the force \(\lambda \) acting on it, where \(c>0\) and \(\alpha \in (0,1)\) are constant. For a springpot, a unit step force input
with the Heaviside step function \(\Theta \) leads to a time-dependent elongation output of the form
Elongation output (13) for a unit step force input \(-\lambda (t)=\Theta (t)\), \(c=1\) and various values of \(\alpha \in [0,1]\)
which shows a behavior “in-between” a spring (\(\alpha =0\)) and a dashpot (\(\alpha =1\)), see Fig. 2. A mechanical interpretation of springpots as an infinite arrangement of springs and dashpots is given in [13, 15, 30, 37] and a related potential energy E, which is useful for the direct method of Lyapunov, can be formulated as
with \(z(\eta ,t)\) as in (3), see [13, 15]. In [11, 40], the energy storage of a fractional element in an electrical circuit was derived, which through the mechanical-electrical analogy, is equivalent to the potential energy (14).
3 Stability of functional differential equations with infinite delay
A reparametrization of (1) using \(s=\tau -t\) leads to the expression
where \(\dot{q}_t(s)=\dot{q}(t+s)\). In that sense, \(\dot{q}_t\) is for each \(t\ge 0\) a function on \((-\infty ,0]\) and the above integral is a functional acting on \(\dot{q}_t\). Furthermore, we consider an autonomous mechanical system with fractional damping described by the equations of motion
with generalized coordinates \(\mathbf {q} \in \mathbb {R}^f\), \(f:=\frac{n}{2}{\in }\mathbb {N}\), a non-singular mass matrix \(\mathbf {M}(\mathbf {q})\) and the vector \(\mathbf {h}\left( \mathbf {q},^C\!\mathrm {D}^\alpha \mathbf {q},\dot{\mathbf {q}}\right) \) including gyroscopic, potential and non-potential forces as well as forces of springpots. A detailed explanation, how springpots (as generalized force laws) can be introduced in the equations of motion, is given in Sect. 4.5. Premultiplying (16) with \((\mathbf {M}(\mathbf {q}))^{-1}\) and using the same notation as in (15), we obtain
where \(\tilde{\mathbf {h}}\) is a functional, that particularly includes the third argument of \(\mathbf {h}\) as \(\dot{\mathbf {q}}(t)=\dot{\mathbf {q}}_t(0)\). The equations of motion can be written in first-order form
with generalized velocities \(\mathbf {v}\in \mathbb {R}^f\). In view of (18) and using the state space notation \(\mathbf {x}=\begin{bmatrix}\mathbf {q}^\mathrm {T}&\mathbf {v}^\mathrm {T}\end{bmatrix}^\mathrm {T}\), we consider an autonomous mechanical system with fractional damping as a so-called (autonomous retarded) functional differential equation (FDE) with infinite delay [3, 4, 9, 19] of the form
with zero initial time, where \(\mathbf {x}_t(s)=\mathbf {x}(t+s)\) for \(s\in (-\infty ,0]\). Herein, the right-hand side is a continuous map
mapping bounded sets into bounded sets, defined on an open subset \(Q_H\subset X\) of the Banach space \({X:=BU((-\infty ,0];\mathbb {R}^n)}\) of bounded uniformly continuous functions mapping \((-\infty ,0]\) to \(\mathbb {R}^n\). We consider the Euclidean norm \(\Vert \cdot \Vert _2\) on \(\mathbb {R}^n\) and the supremum norm \(\Vert \cdot \Vert _\infty \) on X, where
Furthermore, assume that \(Q_H\) is bounded and
A solution of (19) with initial function \(\varvec{\varphi }\in X\) is a function \(\mathbf {x}=\mathbf {x}(\varvec{\varphi })\) defined and continuous on \((-\infty ,T)\) for some \(T>0\) such that \(\mathbf {x}_t(\varvec{\varphi })\in Q_H\) for \(t\in [0,T)\), \(\mathbf {x}_0(\varvec{\varphi })=\varvec{\varphi }\) and \(\mathbf {x}(\varvec{\varphi })(t)\) satisfies (19) for \(t\in [0,T)\). The above choice of the state space X guarantees local existence and uniqueness of solutions if \(\mathbf {f}\) satisfies a local Lipschitz condition [10, 36]. Additionally, we obtain the following important assertion for the case when a solution exists for all \(t\ge 0\).
Proposition 2
Every orbit \(\lbrace \mathbf {x}_t|t\ge 0\rbrace \) in the space\(X=BU((-\infty ,0];\mathbb {R}^n)\) generated by a solution \(\mathbf {x}\) of (19) with \(\mathbf {x}(t)\) bounded on \([0,\infty )\) belongs to a compact subset of X.
The proof of Proposition 2 under more general conditions can be found in [8, 10]. The crucial property of the state space is thereby that the mapping \(t\mapsto \mathbf {x}_t\) is continuous on [0, T) for \(\mathbf {x}=\mathbf {x}(\varvec{\varphi })\) continuous on [0, T) and \(\varvec{\varphi }\in X\). This property is, for example, not fulfilled in the space \(CB((-\infty ,0],\mathbb {R}^n)\) of bounded continuous functions, see [36] and [16, Remark 2.3].We will use the above property in the proof of our main theorem regarding Lyapunov functionals below. First, we introduce stability of FDEs and define invariant sets similar as in [3, 4, 9, 19].
Definition 3
(Stability) Let \(\mathbf {f}(\mathbf {0})=\mathbf {0}\). The trivial solution \(\mathbf {x}(\varvec{\varphi })(t)=\mathbf {0}\) of (19) with initial function \(\varvec{\varphi }\) is called
-
(a)
stable, if for all \(\epsilon \in (0,H]\) there exists a \(\delta =\delta (\epsilon )>0\) such that \(\Vert \mathbf {x}(\varvec{\varphi })(t)\Vert _2<\epsilon \) for \(t\ge 0\) if \(\Vert \varvec{\varphi }\Vert _\infty <\delta \).
-
(b)
locally asymptotically stable, if it is stable and there exists a \(\delta >0\) such that \(\lim \limits _{t\rightarrow \infty }\Vert \mathbf {x}(\varvec{\varphi })(t)\Vert _2=0\) if \(\Vert \varvec{\varphi }\Vert _\infty <\delta \).
-
(c)
globally asymptotically stable, if the condition in (b) holds for all \(\delta \in (0,H]\).
Definition 4
(Limit sets, Invariance)
-
(a)
An element \(\varvec{\psi }\in X\) belongs to the \({\omega }\)-limit set \(\Omega (\varvec{\varphi })\) of \(\varvec{\varphi }\) if \(\mathbf {x}(\varvec{\varphi })\) is defined on \(\mathbb {R}\) and there exists a non-negative sequence \(\lbrace t_j\rbrace _{j\in \mathbb {N}}\), \(t_j \rightarrow \infty \) as \(j\rightarrow \infty \) such that \(\Vert \mathbf {x}_{t_j}(\varvec{\varphi })-\varvec{\psi }\Vert _\infty \rightarrow 0\) as \(j\rightarrow \infty \).
-
(b)
A set \(Q\subset X\) is called invariant if \(\mathbf {x}_t(\varvec{\varphi })\in Q\) for any \({\varvec{\varphi }\in Q}\) and \(t\in [0,\infty )\).
We will now come to the invariance principle for FDEs adapted from [9], which will be instrumental in solving the stability problems for fractionally damped systems in Sects. 4 and 5.
Theorem 5
(Invariance principle) Let \(\mathbf {f}:Q_H\rightarrow \mathbb {R}^n\) be such that \(\mathbf {f}(\mathbf {0})=\mathbf {0}\) and denote \(u:[0,\infty )\rightarrow \mathbb {R}\) some scalar, continuous, non-decreasing function such that \(u(0)=0\), \(u(r)>0\) for \(r>0\) and \(u(r)\rightarrow \infty \) for \(r\rightarrow \infty \). Let there exist a continuous functional \(V:Q_H\rightarrow \mathbb {R}\) with \(V(\mathbf {0})=0\) such that
and let \(\lbrace \mathbf {0}\rbrace \) be the largest invariant set in \(\lbrace \varvec{\varphi }|\dot{V}(\varvec{\varphi })=0\rbrace \). Then, the trivial solution of (19) is globally asymptotically stable.
Herein, \(\dot{V}(\mathbf {x}_t)\) denotes \(\frac{\mathrm {d}}{\mathrm {d}t}(V\circ \mathbf {x})=\frac{\partial V}{\partial \mathbf {x}}\cdot \mathbf {f}(\mathbf {x}_t)\). For the proof of this theorem, we need some properties of the \(\omega \)-limit set of the initial function \(\varvec{\varphi }\) as in the finite-dimensional case.
Proposition 6
Let \(\mathbf {x}(\varvec{\varphi })\) be a solution of (19) with initial function \(\varvec{\varphi }\) and assume \(\{\mathbf {x}_t(\varvec{\varphi })|t\ge 0\}\) belongs to a compact set in \(Q_H\), then \(\Omega (\varvec{\varphi })\) is non-empty, compact, invariant and
The proof of Proposition 6 is similar to the corresponding one in the finite-dimensional case [17, C3] and given in [10, Theorem 3.2]. Herein, Proposition 2 is used.
Proof
(of Theorem 5) For stability, assume any \(\epsilon \in (0,H]\) and choose \(\delta >0\) such that
for \(\Vert \varvec{\varphi }\Vert _\infty <\delta \). Using (23) and (24), we obtain
and the monotonicity of u implies \(\Vert \mathbf {x}(t)\Vert _2\le \epsilon \) for \(t\ge 0\).To prove asymptotic stability, consider the open level sets \(\Omega _c=\{\varvec{\varphi }|V(\varvec{\varphi })<c\}\). For \(\varvec{\varphi }\in \Omega _c\), we have through (23) \(u(\Vert \varvec{\varphi }(0)\Vert _2)< c\) and as \(u(r)\rightarrow \infty \) for \(r\rightarrow \infty \), we can choose \(c>0\) such that \(\Vert \varvec{\varphi }(0)\Vert _2 \le H\). As \(\dot{V}\le 0\) on \(\Omega _c\), \(\mathbf {x}_t(\varvec{\varphi })\in \Omega _c\) for \(t\ge 0\) and hence \(\Vert \mathbf {x}(\varvec{\varphi })(t)\Vert _2\le H\) for \(t\ge 0\) which implies \(\Vert \mathbf {x}_t(\varvec{\varphi })\Vert _\infty {\le }H\). By Proposition 2, \(\{\mathbf {x}_t(\varvec{\varphi })|t\ge 0\}\) belongs to a compact subset of X such that \(V(\mathbf {x}_t(\varvec{\varphi }))\), being non-increasing, is bounded from below and therefore has a limit \(\lim _{t\rightarrow \infty }V(\mathbf {x}_t(\varvec{\varphi }))=a\). By Proposition 6, \(\{\mathbf {x}_t(\varvec{\varphi })|t\ge 0\}\) has a non-empty, compact, invariant \(\omega \)-limit set \(\Omega (\varvec{\varphi })\) which belongs to the aforementioned compact set. This implies for \({\varvec{\psi }\in \Omega (\varvec{\varphi })}\) that \(V(\varvec{\psi })=\lim _{j\rightarrow \infty }V(\mathbf {x}_{t_j}(\varvec{\varphi }))=a\), as V is continuous. Hence, \(V\equiv a\) on \(\Omega (\varvec{\varphi })\) and as \(\Omega (\varvec{\varphi })\) is invariant, we obtain \(\dot{V}=0\) in \(\Omega (\varvec{\varphi })\) and \(\Omega (\varvec{\varphi })\subset \{\mathbf {0}\}\). Again, by Proposition 6, every solution approaches its \(\omega \)-limit set for \(t\rightarrow \infty \). Hence, \(\mathbf {x}_t\) approaches \(\{\mathbf {0}\}\) for \(t\rightarrow \infty \). \(\square \)
Corollary 7
Assume the conditions on \( \mathbf {f}\) and V including (23), (24) as in Theorem 5 and additionally
for some scalar, continuous, non-decreasing function\(\tilde{u}:[0,\infty )\rightarrow \mathbb {R}\) such that \(\tilde{u}(0)=0\), \(\tilde{u}(r)>0\) for \(r>0\). Then, the trivial solution of (19) is globally asymptotically stable.
Proof
The proof starts as in Theorem 5 and condition (27) leads directly to the fact that \(\lbrace \mathbf {0}\rbrace \) is the largest invariant set in \(\lbrace \varvec{\varphi }|\dot{V}(\varvec{\varphi })=0\rbrace \). \(\square \)
4 Application on a damped harmonic oscillator
4.1 Preliminaries
In this section, we want to apply the above stability theorems on a single degree-of-freedom, fractionally damped oscillator (Fig. 3) that fulfills the equations of motion
with mass m, elongation q, damping coefficient d, spring coefficient k, springpot coefficient c and differentiation order \(\alpha \in (0,1)\) and a given continuously differentiable initial function \(\varphi \) such that \(\varphi ,\dot{\varphi }\in BU((-\infty ,0];\mathbb {R})\) and
In view of (15) and (18), we obtain an FDE
with
Using the infinite states in (3) or, equivalently, inserting (5) and
in the last term of (30), we can reformulate the FDE (30) equivalently as
As all the Lyapunov functionals used for the following stability proofs are formulated with the help of the infinite states z and Z from (3) and (9), we prefer the formulation (33) but keep in mind that we can interpret (28) as FDE (30).
In the following, we want to prove asymptotic stability of the trivial equilibrium of (30) for several cases using Theorem 5 and Corollary 7. Hence, to be sure that the right-hand side of (33) is bounded for bounded inputs, we estimate the improper integral by splitting the interval of integration for \(\omega \) in two parts which yields
and
We consider the cases \(d=0\) (no viscous damping), \({d>0}\) (damping) and \(d<0\) (anti-damping) and propose different functionals for the stability and attractivity proofs.
4.2 No viscous damping
First, we consider (28) for the case \(d=0\) and use the total mechanical energy
as a Lyapunov functional as in [13, 15], which contains the potential energy (14) of the springpot. The notation of the arguments in (34) is adapted from Sect. 3. We prove asymptotic stability of the trivial solution with the help of Theorem 5. It is obvious that inequality (23) holds for \(V_1\). Furthermore, as
inequality (24) is fulfilled, such that the trivial solution is stable. Moreover, examine the largest invariant set in \({\lbrace \dot{V}_1=0\rbrace }\). From (35), we conclude
and substitution in the z-dynamics of (3) results in
which together with (28) implies that \(\lbrace \mathbf {0}\rbrace \) is the largest invariant set in \(\lbrace \dot{V}_1=0\rbrace \). Finally, all conditions of Theorem 5 are fulfilled and the trivial solution is globally asymptotically stable. Note that \(\dot{V}_1\) in (35) can be interpreted as internal power losses of the springpot, see [13, 30, 37] or for an analogue electrical system [11, 40].
4.3 Viscous damping
Using the energy functional \(V_1\) in the case \(d>0\) again leads to a non-positive rate of \(V_1\)
which proves asymptotic stability of the equilibrium using the same arguments as for the case without viscous damping. Alternatively, we propose an augmented candidate Lyapunov functional which contains the potential energy term (14) to prove asymptotic stability with the help of Corollary 7. Therefore, the functional includes an additional term using the infinite states from (9). It has the form
We check the assumptions in Theorem 5 and Corollary 7. For (23) we can estimate
such that (23) is fulfilled. Moreover, we compute the rate of \(V_2\) along solution curves
which proves (27) and using Corollary 7 leads to global asymptotic stability of the trivial equilibrium. The particular structure of the functional \(V_2\) in (39) is revisited for a stability proof in Sect. 5.
4.4 Viscous anti-damping
For the case \(d<0\), whose physical interpretation is explained and motivated in [15, Sect. 4.5.3], we expect the equilibrium of (28) to remain stable only for certain values of d. The detailed requirements on the parameters in (28) to ensure stability have been derived in [15] using the Laplace transform method and a special Lyapunov functional. The result is formulated in the following assertion.
Proposition 8
Let \(m,k,c>0,\ \alpha \in (0,1)\) and let \({r=r_*>0}\) be the solution of
Let \(d\in \mathbb {R}\) be such that the inequality
holds. Then, the trivial solution of (28) is globally asymptotically stable.
From the above statement, it follows that a springpot can stabilize an oscillator up to a critical negative viscous damping with coefficient
We conclude that we may regard (43) as the equivalent viscous damping capability of a springpot. The dependency of \(d_\mathrm {crit}\) on \(\alpha \in (0,1)\) may change drastically for different parameter sets, and it is quite interesting that the magnitude of \(d_\mathrm {crit}\) can become greater than c for certain values of \(\alpha \), i.e., a springpot can induce a higher rate of dissipation than a dashpot with the same coefficient [15]. For the proof of Proposition 8 with the help of the direct method of Lyapunov, the energy functional is not usable any more, as anti-damping can lead to an increasing energy in some time intervals, see [43]. Therefore, we introduce another Lyapunov functional, which will be motivated by a reformulation of the fractional derivative. Moreover, we will need the following auxiliary propositions.
Proposition 9
Proof
Due to the relation for the Laplace transform of \(\mathrm {e}^{-\omega t}\)
we obtain (44) using the formula
and Fubini’s Theorem as
Proposition 10
For \(\alpha \in (0,1)\) and \(r>0\), the identities
hold.
Proof
Substitute \(\eta =\omega ^2\) and \(\mathrm {d}\eta =2\omega \,\mathrm {d}\omega \) in the integral and obtain
Using the sine-double-angle formula and (44), we directly obtain (45). The proof of (46) is analogous. \(\square \)
Remark 11
Similar assertions as in Proposition 10 are proven in [43].
In the following, let \(r_*\) be the solution of (41). We reformulate the fractional derivative using equations (3), (9) and Proposition 10 as
Therein, we detect new improper integrals of the infinite states with a new integration kernel which we call
This leads to a reformulation of the equation of motion (28) as
which contains modified stiffness and damping parameters
Obviously, the modified stiffness parameter \(\tilde{k}\) is positive, while the modified damping parameter \(\tilde{d}\) becomes non-positive for \(d\le d_\mathrm {crit}\). A coordinate transformation to modified positions
and modified velocities
transforms (49) to a reformulated system
in first-order form. Note that the first equation in (53) holds because \(mr_*^2=\tilde{k}\), as \(r_*\) is the solution of (41). We are now ready to give the Lyapunov proof of asymptotic stability.
Proof
(of Proposition 8) Again, we show that all conditions in Theorem 5 are fulfilled. Consider the candidate Lyapunov functional
and prove inequality (23) for \(V_3\) w.r.t. the functions \(q_t\) and \(v_t\). Hereto, consider the split of the integral term in (54)
and use the mean value theorem for the first term and the inequality \(\omega \ge 1\) in the second term to find a constant \({\tilde{C}\in (0,1]}\), such that
Moreover, we use Hölder’s inequality and Proposition 10 to obtain
and
By splitting the third term in (54) in two equal parts, estimating the first with (56) and the second with (57), we may estimate (54) as
Finally, applying the general relation
for \(a,b,\gamma \in {\mathbb {R}},\ \gamma >0\) on the first two and the last two terms of (58) using (51) and (52), we obtain inequality (23) for \(V_3\). Furthermore, we compute the rate of \(V_3\) as
Inserting the dynamics from (53), we obtain
Again, Hölder’s inequality and Proposition 10 lead to
and we finally obtain
where due to (41)
Hence, we obtain (24) for \(d>d_\mathrm {crit}\) and, using the same arguments as in Sect. 4.2, we conclude that \(\lbrace \mathbf {0}\rbrace \) is the largest invariant set in \(\lbrace \dot{V}_3=0\rbrace \) such that all conditions of Theorem 5 are fulfilled. This leads to the proof of global asymptotic stability of the trivial equilibrium. \(\square \)
Finally, we have found a Lyapunov functional \(V_3\), such that \(\dot{V}_3\le 0\), which has the form of an energy functional w.r.t. the new coordinates \(\tilde{q}_t\) and \(\tilde{v}_t\) and, using Theorem 5, we conclude global asymptotic stability. In [15], we used a non-autonomous version of Corollary 7 for the stability proof by introducing the more elaborate Lyapunov functional
which fulfills (27) for \(d>d_\mathrm {crit}\), see [15] for the details. However, the invariance principle renders the use of \(V_4\) redundant for the proof. In summary, the Lyapunov proofs in this section lead to the following conclusions.
Remark 12
-
(a)
The energy of a springpot (14) and the infinite states \(z(\eta ,\cdot )\) in (3) and \(Z(\eta ,\cdot )\) in (9), \(\eta >0\) are valuable expressions for the formulation of Lyapunov functionals for fractionally damped systems.
-
(b)
The conditions for asymptotic stability in Proposition 8 are equivalent to the necessary and sufficient conditions obtained by the eigenvalue analysis in [15]. Furthermore, it is possible to obtain the same conditions using the energy balance principle as it was done in [42, 43] for an electrical system. As such, the choice of the functional \(V_3\) is optimal to estimate the critical negative damping parameter. Moreover, the direct method of Lyapunov has advantages over an eigenvalue analysis or the energy balance principle, as it can lead to global stability results in the nonlinear case, avoids the cumbersome computation of eigenvalues and may even give results in the non-hyperbolic case where an eigenvalue analysis fails.
-
(c)
As already mentioned in Remark 1, the initialization in (1) leads to an autonomous FDE and thereby allows for the use of an invariance principle (Theorem 5) to prove asymptotic stability. This leads to an easier reasoning than in [15], where a finite-history approach for the fractional derivative resulted in non-autonomous FDEs.
-
(d)
The reformulation in (47) leads to a novel representation of the fractional derivative with two advantages (besides the Lyapunov stability proof). First, the reformulation extracts the stiffness and viscous damping behavior of a springpot through the parameters \(\tilde{k}\) and \(\tilde{d}\) in (50) leading to an improved mechanical interpretation of fractional damping. Second, the improper integrals of the infinite states contain a new kernel \(\mathrm {K}\) as in (48), which, in contrast to (4), is integrable and asymptotically decays to zero. These properties lead to advantages for a quadrature of the integrals and are the basis for a novel numerical scheme to solve ordinary differential equations containing fractional derivatives that we proposed in [14].
4.5 Generalization for linear finite-dimensional mechanical systems
We want to extend the proposed Lyapunov approach for the one-dimensional case to a general linear mechanical system
with generalized coordinates \(\mathbf {q}\in \mathbb {R}^f\), mass matrix \(\mathbf {M}\), damping matrix \(\mathbf {D}\), gyroscopic matrix \(\mathbf {G}\), stiffness matrix \(\mathbf {K}\), springpot coefficient c and differentiation order \(\alpha \), where \(\mathbf {M}\), \(\mathbf {D}\) and \(\mathbf {K}\) are constant symmetric positive definite matrices and \(\mathbf {G}=-\mathbf {G}^\mathrm {T}\) is a constant skew-symmetric matrix in \(\mathbb {R}^{f\times f}\). Furthermore, consider a generalized force \(\mathbf {W}\lambda \) with constant generalized force direction \(\mathbf {W}\in \mathbb {R}^{f\times 1}\) and a force law \(\lambda \) of a springpot with elongation g that fulfills the linear geometric relation
To prove stability of the trivial equilibrium, we proceed as in Sects. 4.2 and 4.3 using infinite states (3) and the energy Lyapunov functional
that fulfills (23) as \(\mathbf {K}\), \(\mathbf {M}\) are positive definite and (24) as
As \(\mathbf {D}\) is positive definite and \(c>0\), again \(\lbrace \mathbf {0}\rbrace \) is the largest invariant set in \(\lbrace \dot{V}_5=0\rbrace \) and asymptotic stability of the trivial equilibrium can be concluded using Theorem 5 as before.
Hereafter, we generalize the case of anti-damping from Sect. 4.4. Therefore, let \(\mathbf {M}\) and \(\mathbf {K}\) be symmetric and positive definite as before, whereas \(\mathbf {G}=\mathbf {0}\) and \(\mathbf {D}\) is symmetric but has one (possibly) non-positive eigenvalue
with normalized eigenvector \(\mathbf {W}\), \(\mathbf {W}^\mathrm {T}\mathbf {W}=1\), where \(r_*\) solves the generalized eigenvalue problem
such that \(\mathbf {W}\) is an eigendirection of \(\mathbf {K}\) (with eigenvalue k) and \(\mathbf {M}\) (with eigenvalue m) as well, i.e., \(r_*\) is the solution of (41) as in the one-dimensional case. Using the representation (47) of the fractional derivative and the infinite states (3), we can reformulate (63) as
with new stiffness and damping matrices
which both are symmetric and positive definite. Again, a coordinate transformation
results, using (68) in the modified equations of motion
From the assumptions above, we directly obtain
which leads to the Lyapunov functional
Similar as for \(V_3\), we can show (23) for \(V_6\) as \(\tilde{\mathbf {K}}\), \(\mathbf {M}\) are positive definite and estimate its time derivative inserting the dynamics (72) and using (60), (68) as
such that (24) is satisfied and \(\lbrace \mathbf {0}\rbrace \) is the largest invariant set in \(\lbrace \dot{V}_6=0\rbrace \). Using Theorem 5, we conclude asymptotic stability as usual. A further generalization for several springpot elements is straightforward.
5 Tracking control
5.1 Preliminaries
In the following section, we apply the Lyapunov approach derived for fractionally damped mechanical systems on a more general tracking control problem with fractional and nonlinear damping. The basic ideas for the construction of Lyapunov functionals are similar to those presented so far.
5.2 Statement of the problem
5.2.1 Classical formulation of a Lur’e system
The following paragraph summarizes well-known results regarding the stability of Lur’e systems, see, e.g., [17] for a more in-depth exposition. Moreover, it is meant as an introduction to certain controlled dynamical systems and the notion of convergence [32], before we generalize these concepts for the fractionally damped case in subsequent sections. A Lur’e system, in the classical sense, is the connection of a linear system and an output dependent nonlinearity of the form
where \(\mathbf {x}\in \mathbb {R}^n\) is the system state, \(w\in \mathbb {R}\) the (single) input and \(y\in \mathbb {R}\) the (single) output of the system. Furthermore, the system matrices \(\mathbf {A}\), \(\mathbf {B}\), \(\mathbf {C}\), \(\mathbf {D}\) are considered to be constant and the pair \((\mathbf {A},\mathbf {B})\) is controllable, \((\mathbf {A},\mathbf {C})\) is observable. The nonlinearity \(\phi =\phi (y)\) is a continuous function of the output y with \(\phi (0)=0\). The uniform asymptotic stability of the origin of (76) (in the absence of the input w) for a certain class of nonlinearities \(\phi \) is called absolute stability, named after Lur’e who originally formulated the problem [17]. A related task is the formulation of conditions on (76) such that for a class of inputs w(t) asymptotic stability of all solutions is guaranteed [48]. This leads to the more general notion of convergent systems as defined in [32].
Definition 13
(Convergence) A nonlinear system
is called (uniformly) convergent for a class of piecewise continuous and bounded inputs \(\mathcal {N}\), if there exists a solution \(\bar{\mathbf {x}}_w(t)\) that is defined and bounded for all \(t\in \mathbb {R}\) and globally (uniformly) asymptotically stable for every input \(w\in \mathcal {N}\).
Hence, for a (uniformly) convergent system, the solution \(\bar{\mathbf {x}}_w(t)\) is the unique steady-state solution. For a uniformly convergent system, it is known that a constant input w(t) leads to a constant steady-state solution and a periodic input w(t) with period time T results in a periodic steady-sate solution with the same period T [32]. A specific task using known results on convergence is to solve the tracking problem for (76), i.e., to design a control law w(t) such that a desired solution \(\mathbf {x}_\mathrm {d}(t)\) is globally asymptotically stable for a certain class of nonlinearities \(\phi \). In this paper, we consider monotonically non-decreasing functions \(\phi \) such that
For this case, it can be shown that the tracking problem can be solved using a combination of linear tracking error-feedback and feedforward control in the form
where \(\mathbf {K}\in \mathbb {R}^{1\times n}\) is the feedback gain matrix and \(w_\mathrm {ff}\) the feedforward control. Together with (76), we obtain the closed-loop dynamics
where
The feedforward \(w_\mathrm {ff}(t)\) in (78) is chosen such that \(\mathbf {x}_\mathrm {d}(t)\) is a solution of (79) and the control gain \(\mathbf {K}\) is designed such that all solutions of (79) approach \(\mathbf {x}_\mathrm {d}(t)\), i.e., (79) is a convergent system. To give sufficient conditions for convergence of (79), we consider the incremental Lyapunov function of two solutions \(\mathbf {x}_1\) and \(\mathbf {x}_2\) as
where \(\mathbf {P}\) is symmetric and positive definite. Straightforward application of the direct method of Lyapunov [17, Theorem 4.1] leads to the following absolute stability result of Yakubovich [48] (see also [31] for a historic review).
Theorem 14
Consider the system (79) with (77), (80), where \(w_\mathrm {ff}\) is chosen such that \(\mathbf {x}_\mathrm {d}\) is a bounded continuous solution of (79). If there exists a symmetric, positive definite matrix \(\mathbf {P}\) and a feedback gain \(\mathbf {K}\) such that the relations
hold, then all solutions of (79) asymptotically approach \(\mathbf {x}_\mathrm {d}(t)\).
Proof
The Lyapunov function (81) is a positive definite function of the error between two solutions, and it fulfills
where we inserted (83) in the last line. Using the monotonicity condition (77) and (82), we conclude that \(-\dot{V}_7\) is positive definite, and hence, according to a classical Lyapunov theorem [17, Theorem 4.1], the tracking error dynamics is globally asymptotically stable, and particularly, the bounded solution \(\mathbf {x}_\mathrm {d}\) is asymptotically approached by all solutions of (79). \(\square \)
5.2.2 Case of fractional damping
We try to generalize the above results for a class of fractionally damped nonlinear systems of the form
where again \(\mathbf {x}\in \mathbb {R}^n\) is the system state, \(w\in \mathbb {R}\) the (single) input, \(y\in \mathbb {R}\) and \(g\in \mathbb {R}\) the outputs of the linear system and \(\mathbf {A}\), \(\mathbf {B}\), \(\mathbf {C}\), \(\mathbf {D}\), \(\mathbf {E}_0\), \(\mathbf {E}_1\), \(\mathbf {F}\) are constant matrices that fulfill
Furthermore, \(^C\!\mathrm {D}^\alpha g\) is the fractional derivative of the elongation g of a springpot and \(\phi =\phi (y)\) is a nonlinear function of the output y that fulfills (77). Again, we consider the problem of tracking a desired solution \(\mathbf {x}_\mathrm {d}(t)\) of (85) using a control law of the form (78), which leads to the closed-loop dynamics
with \(\mathbf {A}_\mathrm {cl}\) as in (80). As before, the feedforward \(w_\mathrm {ff}(t)\) in (78) is chosen such that \(\mathbf {x}_\mathrm {d}(t)\) is a solution of (87) and the control gain \(\mathbf {K}\) is designed to render (87) convergent. Sufficient conditions for that will be given with the help of a Lyapunov functional inspired from (81) and adapted to the fractional derivative terms in (87). Hereto, we consider the infinite states
of a springpot as in (3), such that
and the second kind of infinite states
as in (9). This leads together with (87) to the reformulated system
To give sufficient conditions for convergence of (91), we consider the incremental Lyapunov functional of two solutions \(\mathbf {x}_1\) and \(\mathbf {x}_2\) as
where \(\mathbf {P}\) is symmetric, positive definite and \(\delta _0\ge 0\), \(\delta _1>0\). The time derivative of \(V_8\) along solutions of (91) results in
From the terms in (93), we can extract conditions for convergence of (91), which are formulated in the following theorem.
Theorem 15
Consider the system (91) with (77), (80), where \(w_\mathrm {ff}(t)\) is chosen such that \(\mathbf {x}_\mathrm {d}(t)\) is a bounded continuous solution of (91). If there exists a symmetric, positive definite matrix \(\mathbf {P}\), coefficients \(\delta _0\ge 0\), \(\delta _1>0\) and a feedback gain \(\mathbf {K}\) such that the relations
hold, then all solutions of (91) asymptotically approach \(\mathbf {x}_\mathrm {d}(t)\).
The condition (94) is weaker than the classical Lyapunov inequality (82) in Theorem 14. Hence, for the theorem to hold we need the generalized invariance principle in Theorem 5 to prove asymptotic stability.
Proof
(of Theorem 15) Initially, we have to guarantee that the right-hand side of (91) is bounded for bounded inputs. The proof is similar as for the single degree-of-freedom oscillator in Sect. 4. The Lyapunov functional given in (92) is formulated in two solutions \(\mathbf {x}_1\) and \(\mathbf {x}_2\) of (91). Fixing one of these solutions, we can prove asymptotic stability of the error dynamics between the fixed and any other solution using Theorem 5. From the definition of the Lyapunov functional \(V_8\) in (92), it is clear that (23) is satisfied. Furthermore, using (77), (94), (95) and (96) in (93), we obtain (24) as
Subsequently, we examine the largest invariant set in \({\lbrace \dot{V}_8=0\rbrace }\). From the last term in (98), we conclude
and substitution of (99) in the z-dynamics of (91) leads to
Moreover, using (100) in the \(\mathbf {x}\)-dynamics of (91) results in
where the nonlinear terms vanish as the second term in (98) has to vanish on \(\lbrace \dot{V}_8=0\rbrace \). Considering the first term in (98) and using condition (97), we obtain that \(\lbrace \mathbf {x}_1=\mathbf {x}_2\rbrace \) is the largest invariant set in \(\lbrace \dot{V}_8=0\rbrace \). From Theorem 5, we conclude that all solutions of (91) converge to each other. As \(\mathbf {x}_\mathrm {d}\) is a bounded solution of (91), all solutions asymptotically approach \(\mathbf {x}_\mathrm {d}\). \(\square \)
5.3 Tracking control of a motor–load archetype system
We consider a typical motor–load configuration where the nonlinear damping \(\lambda \) and the actuation w are non-collocated (Fig. 4), inspired from the example in [22, Sect. 8.4.2]. Herein, the translational motion of two interconnected masses, representing motor and load, is considered, being mechanically equivalent to its rotational counterpart. The aim in this tracking problem is to track the (translational resp. rotational) velocity of the load and not its position. Following [22], we consider two masses \(m_1\) and \(m_2\) with coordinates \(q_1\) and \(q_2\) which are linked by a spring (stiffness k). The first mass is actuated by a control force w and on the second mass acts a nonlinear damping force \(-\lambda =\phi (\dot{q}_2)\) that fulfills (77). We generalize the results in [22] by replacing the dashpot between the two masses by a springpot (coefficient \(c>0\), differentiation order \(\alpha \in (0,1)\)). Using the law of linear momentum, we obtain a system of the form (85), where
and \(\mathbf {x}=\begin{bmatrix}q_2-q_1&\dot{q}_1&\dot{q}_2 \end{bmatrix}^\mathrm {T}\). Note that this state vector does not contain the absolute positions \(q_1\) and \(q_2\) as we aim at velocity tracking.
Initially, we want to track a stationary solution with desired velocity \(v_\mathrm {d}\) (for both masses). Therefore, we introduce a control law (78) and reformulate our system as in (91). Related to the desired solution of constant velocity is an equilibrium of (87)
when we use a feedforward control
When choosing
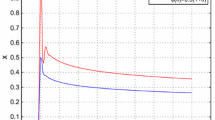
Tracking of \(\dot{q}_{2,d}\) from (112) with feedforward (left) or feedback and feedforward control (right)
together with the feedback gain
all conditions in Theorem 15 are fulfilled. In particular,
We implement the control law given above to simulate the solutions of the closed loop system (91) with (102), parameters
desired velocity \(v_\mathrm {d}=1\,\mathrm {\frac{m}{s}}\) and a nonlinearity
that models regularized Coulomb friction for the second mass. We use the numerical scheme proposed in [14] and show tracking in Fig. 5 for the initial conditions
We observe that even without feedback control, tracking is achieved (although much slower), as the nonlinearity contributes to the attractivity of \(\mathbf {x}_\mathrm {d}\).
In a second step, we want to illustrate that the feedback gain (106) can be used to stabilize any bounded time-varying desired solution \(\mathbf {x}_\mathrm {d}\). However, for a non-constant desired solution the determination of the associated feedforward \(w_\mathrm {ff}\) becomes cumbersome and generally has to be computed numerically. Here, we provide an example with solution in closed form. We consider the nonlinear damping
and a desired oscillating velocity of the second mass
Using the harmonic balance method, we obtain the associated desired trajectory \(\mathbf {x}_\mathrm {d}=\begin{bmatrix} x_{\mathrm {d},1}&x_{\mathrm {d},2}&x_{\mathrm {d},3}\end{bmatrix}^\mathrm {T}\) with
and the feedforward
with coefficients
Using parameters as in (108) together with
and initial conditions (110), we obtain tracking (with and without feedback) as shown in Fig. 6. The addition of feedback greatly ameliorates the tracking speed.
6 Conclusion
This article provides an introduction to the direct method of Lyapunov for nonlinear dynamical systems with fractional damping and, at the same time, extends the existing results. The ingredients for the novel outcome are the Lyapunov theory of functional differential equations and a class of (energy-like) Lyapunov functionals formulated with the help of the infinite state representation of fractional derivatives. The method is applied on the fundamental mechanical problem of a harmonic oscillator and generalized for a finite-dimensional linear mechanical and a nonlinear controlled dynamical system.
A particular application of the theory and original result of this paper is the solution of a tracking control problem for an archetype fractionally damped mechanical system with regularized Coulomb friction using feedforward and feedback control. Thereby, the design of the feedback gain can be deduced directly from the chosen Lyapunov functional of the stability proof. The determination of the feedforward can be a challenging task though, depending on the desired trajectory. A possible generalization could be the introduction of maximal monotone set-valued Coulomb friction laws as in [22]. Therefore, a generalized Lyapunov theory for FDE control systems with set-valued inputs is required, which seems to be an ambitious project itself.
Another interesting question is, whether the method is still applicable for certain non-monotone friction laws with partly negative slope (Stribeck effect) in the general finite-dimensional case. An indication that this may be possible is given at the end of [15].
References
Angeli, D.: A Lyapunov approach to incremental stability properties. IEEE Trans. Autom. Control 47(3), 410–421 (2002)
Bagley, R.L., Torvik, P.J.: Fractional calculus in the transient analysis of viscoelastically damped structures. AIAA J. 23(6), 918–925 (1985)
Burton, T.A.: Stability and Periodic Solutions of Ordinary and Functional Differential Equations. Mathematics in Science and Engineering, vol. 178. Academic Press, Orlando (1985)
Burton, T.A.: Volterra Integral and Differential Equations. Mathematics in Science and Engineering, vol. 202. Elsevier, Amsterdam (2005)
Caputo, M.: Linear models of dissipation whose \(Q\) is almost frequency independent - II. Geophys. J. Int. 13(5), 529–539 (1967)
Diethelm, K.: The Analysis of Fractional Differential Equations: An Application-Oriented Exposition Using Differential Operators of Caputo Type. Lecture Notes in Mathematics, vol. 2004. Springer, Berlin (2010)
Duarte-Mermoud, M.A., Aguila-Camacho, N., Gallegos, J.A., Castro-Linares, R.: Using general quadratic Lyapunov functions to prove Lyapunov uniform stability for fractional order systems. Commun. Nonlinear Sci. Numer. Simul. 22, 650–659 (2015)
Hale, J.K.: Dynamical systems and stability. J. Math. Anal. Appl. 26, 39–59 (1969)
Hale, J.K.: Theory of FunctionalDifferential Equations. Applied Mathematical Sciences, vol. 3, 2nd edn. Springer, New York (1977)
Hale, J.K., Kato, J.: Phase space for retarded equations with infinite delay. Funkcialaj Ekvacioj 21, 11–41 (1978)
Hartley, T.T., Trigeassou, J.C., Lorenzo, C.F., Maamri, N.: Energy storage and loss in fractional-order systems. J. Comput. Nonlinear Dyn. 10(6), 061006 (2015)
Hilfer, R. (ed.): Applications of Fractional Calculus in Physics. World Scientific, Singapore (2000)
Hinze, M., Schmidt, A., Leine, R.I.: Mechanical representation and stability of dynamical systems containing fractional springpot elements. In: Proceedings of the IDETC Quebec, Canada (2018)
Hinze, M., Schmidt, A., Leine, R.I.: Numerical solution of fractional-order ordinary differential equations using the reformulated infinite state representation. Fract. Calc. Appl. Anal. 22(5), 1321–1350 (2019)
Hinze, M., Schmidt, A., Leine, R. I.: Lyapunov stability of a fractionally damped oscillator with linear (anti-)damping, Int. J. Nonlinear Sci. Numer. Simul. (2020). https://doi.org/10.1515/ijnsns-2018-0381
Kappel, F., Schappacher, W.: Some considerations to the fundamental theory of infinite delay equations. J. Differ. Equ. 37, 141–183 (1980)
Khalil, H.K.: Nonlinear Systems, 3rd edn. Prentice Hall, Upper Saddle River (2002)
Koeller, R.C.: Applications of fractional calculus to the theory of viscoelasticity. J. Appl. Mech. 51(2), 299–307 (1984)
Kolmanovskii, V.B., Nosov, V.R.: Stability of Functional Differential Equations. Mathematics in Science and Engineering, vol. 180. Academic Press, London (1986)
Lakshmikantham, V., Leela, S., Devi, J.V.: Theory of Fractional Dynamic Systems. Cambridge Scientific Publications, Cambridge (2009)
LaSalle, J.P., Artstein, Z.: The Stability of Dynamical Systems. Regional Conference Series in Applied Mathematics, vol. 25. Society for Industrial and Applied Mathematics, Philadelphia (1976)
Leine, R.I., van de Wouw, N.: Stability and Convergence of Mechanical Systems with Unilateral Constraints. Lecture Notes in Applied and Computational Mechanics, vol. 36. Springer, Berlin (2008)
Li, Y., Chen, Y.Q., Podlubny, I.: Stability of fractional-order nonlinear dynamic systems: Lyapunov direct method and generalized Mittag-Leffler stability. Comput. Math. Appl. 59(5), 1810–1821 (2010)
Lorenzo, C.F., Hartley, T.T.: Initialization of fractional-order operators and fractional differential equations. J. Comput. Nonlinear Dyn. 3(2), 021101 (2008)
Matignon, D.: Stability results for fractional differential equations with applications to control processing. In: Computational Engineering in Systems Applications Multiconference, IMACS, IEEE-SMC, Lille, France, pp. 963–968 (1996)
Matignon, D.: Stability properties for generalized fractional differential systems. ESAIM Proc. 5, 145–158 (1998)
Monje, C.A., Chen, Y., Vinagre, B.M., Xue, D., Feliu-Batlle, V.: Fractional-Order Systems and Controls: Fundamentals and Applications. Springer, Berlin (2010)
Montseny, G.: Diffusive representation of pseudo-differential time-operators. Proc. ESSAIM 5, 159–175 (1998)
Oldham, K., Spanier, J.: The Fractional Calculus: Theory and Applications of Differentiation and Integration to Arbitrary Order. Elsevier, New York (1974)
Papoulia, K.D., Panoskaltsis, V.P., Kurup, N.V., Korovajchuk, I.: Rheological representation of fractional order viscoelastic material models. Rheol. Acta 49(4), 381–400 (2010)
Pavlov, A., Pogromsky, A., van de Wouw, N., Nijmeijer, H.: Convergent dynamics, a tribute to Boris Pavlovich Demidovich. Syst. Control Lett. 52, 257–261 (2004)
Pavlov, A., van de Wouw, N., Nijmeijer, H.: Uniform Output Regulation of Nonlinear Systems: A Convergent Dynamics Approach. Systems and Control: Foundations & Applications. Birkhäuser, Boston (2006)
Podlubny, I.: Fractional Differential Equations: An Introduction to Fractional Derivatives, Fractional Differential Equations, to Methods of their Solution and Some of their Applications. Mathematics in Science and Engineering, vol. 198. Academic Press, San Diego (1999)
Sabatier, J., Moze, M., Farges, C.: LMI stability conditions for fractional order systems. Comput. Math. Appl. 59(5), 1594–1609 (2010)
Samko, S.G., Kilbas, A.A., Marichev, O.I.: Fractional Integrals and Derivatives: Theory and Applications. Gordon and Breach, Yverdon (1993)
Sawano, K.: Some considerations on the fundamental theorems of functional differential equations with infinite delay. Funkcialaj Ekvacioj 25, 97–104 (1982)
Schiessel, H., Blumen, A.: Hierarchical analogues to fractional relaxation equations. J. Phys. A Math. General 26(19), 5057–5069 (1993)
Schmidt, A., Gaul, L.: Finite element formulation of viscoelastic constitutive equations using fractional time derivatives. Nonlinear Dyn. 29(1), 37–55 (2002)
Sun, H., Zhang, Y., Baleanu, D., Chen, W., Chen, Y.: A new collection of real world applications of fractional calculus in science and engineering. Commun. Nonlinear Sci. Numer. Simul. 64, 213–231 (2018)
Trigeassou, J.C., Maamri, N.: Analysis, Modeling and Stability of Fractional Order Differential Systems 2: The Infinite State Approach. Wiley, New York (2020)
Trigeassou, J.C., Maamri, N., Oustaloup, A.: Initialization of Riemann–Liouville and Caputo fractional derivatives. In: ASME 2011 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, pp. 219–226 (2011)
Trigeassou, J.C., Maamri, N., Oustaloup, A.: Lyapunov stability of commensurate fractional order systems: a physical interpretation. J. Comput. Nonlinear Dyn. 11(5), 051007 (2016)
Trigeassou, J.C., Maamri, N., Oustaloup, A.: Lyapunov stability of noncommensurate fractional order systems: an energy balance approach. J. Comput. Nonlinear Dyn. 11(4), 041007 (2016)
Trigeassou, J.C., Maamri, N., Sabatier, J., Oustaloup, A.: A Lyapunov approach to the stability of fractional differential equations. Signal Process. 91(3), 437–445 (2011)
Trigeassou, J.C., Maamri, N., Sabatier, J., Oustaloup, A.: State variables and transients of fractional order differential systems. Comput. Math. Appl. 64(10), 3117–3140 (2012)
Trigeassou, J.C., Maamri, N., Sabatier, J., Oustaloup, A.: Transients of fractional-order integrator and derivatives. Signal Image Video Process. 6(3), 359–372 (2012)
Weyl, H.: Bemerkungen zum Begriff des Differentialquotienten gebrochener Ordnung. Vierteljschr. Naturforsch. Gesellsch. Zurich 62, 296–302 (1917)
Yakubovich, V.A.: The matrix-inequality method in the theory of the stability of nonlinear control systems I. The absolute stability of forced vibrations. Autom. Rem. Control 25(7), 905–917 (1964)
Acknowledgements
This work is supported by the Federal Ministry of Education and Research of Germany (BMBF) under Grant Number 01IS17096B.
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Hinze, M., Schmidt, A. & Leine, R.I. The direct method of Lyapunov for nonlinear dynamical systems with fractional damping. Nonlinear Dyn 102, 2017–2037 (2020). https://doi.org/10.1007/s11071-020-05962-3
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11071-020-05962-3
Keywords
- Fractional damping
- Springpot
- Lyapunov functional
- Functional differential equation
- Invariance principle
- Tracking control