Abstract
This paper is concerned with nonlinear modeling and analysis of the COVID-19 pandemic currently ravaging the planet. There are two objectives: to arrive at an appropriate model that captures the collected data faithfully and to use that as a basis to explore the nonlinear behavior. We use a nonlinear susceptible, exposed, infectious and removed transmission model with added behavioral and government policy dynamics. We develop a genetic algorithm technique to identify key model parameters employing COVID-19 data from South Korea. Stability, bifurcations and dynamic behavior are analyzed. Parametric analysis reveals conditions for sustained epidemic equilibria to occur. This work points to the value of nonlinear dynamic analysis in pandemic modeling and demonstrates the dramatic influence of social and government behavior on disease dynamics.
Similar content being viewed by others
1 Introduction
Coronavirus disease 2019 (COVID-19) is an infectious disease caused by Severe Acute Respiratory Syndrome CoronaVirus 2 (SARS-CoV-2) that was first identified in China in early December 2019. It has since become a global pandemic devastating the health, economy and lives of billions of people all over the world and has brought into sharp focus the need for accurate modeling of infectious diseases. The global government policies are in fact largely being driven by statistical analyses loosely based on nonlinear mathematical models that underlie epidemiology. As we write this paper, there is also a rising controversy about the predictive power of these models. The crux of the matter is that there is a trade-off between economic disruptions and deaths. If the model predictions are incorrect in terms of overprediction, we may be creating mass unemployment and hurting billions of lives by causing economic deprivation. On the other hand, if the model predictions are wrong through underprediction, then too many unnecessary deaths would occur. This quandary that most political leaders are finding themselves in points to the need for high accuracy in the models.
Mathematical modeling in epidemiology has a long history dating back to early models by Bernoulli in the eighteenth century [1, 2], although most current research uses models built on those developed in the 1930s by Kermack and McKendrick [3,4,5]. These are called compartment models and constitute a set of nonlinear ordinary differential equations, where the state variables represent the population numbers in various stages of the infectious disease progression, which are described below [6].
-
Susceptible individuals (S). There is no detectable level of pathogens, and the individual’s immune system has not developed a specific response to the disease-causing pathogen.
-
Exposed individuals (E). The individual has come into contact with an infected person and is infected, but exhibits no obvious symptoms and has low levels of the pathogen that is not high enough to sustain a transmission to other hosts.
-
Infected individuals (I). The number of pathogens has increased to a point that it is now possible to transmit to other susceptible individuals.
-
Removed individuals (R). The individual’s immune system has possibly won the battle and reduced the number of parasites significantly, and he/she is no longer infectious. Or, the individual has been isolated from the population, or, alas, he/she has succumbed to the disease and died. In all of these cases, the individual is said to be removed.
Note that it is common practice to model the number of individuals in each of the above categories as fractions of the nominal population. We should also observe that other potential variables could be included to account for quarantines, vaccination, etc. The key factors that govern the dynamics are the growth rate of the pathogen and the level of interaction between the pathogen and the host’s immune response.
As in all modeling, we will have to make a compromise between predictive accuracy and complexity. In addition, since we are using real data, the task of estimating accurate parameters becomes intractable, if not impossible, with a very complex model. Considering all these factors, we will consider a SEIR model (describing susceptible, exposed, infected and removed individuals) as described further in the sequel. We will modify the SEIR model with two important features: the effect of government action and that of public reaction. These two behavioral actions represent social dynamical variables and are especially relevant to the accuracy of predictions as we will show. Of all the nonlinear phenomena we may expect to find, it is important to note that endemic equilibrium points are probably most critical to identify; that is to say, we are interested in knowing under what conditions the disease will persist, and not vanish.
Particularly with growing interest in the impact of the COVID-19 virus, there has been an explosion of research papers in modeling and prediction. It is hence not possible to refer to all—or even a large percentage—of them. What follows is hence a snapshot focusing somewhat on the subject of the current paper.
As mentioned earlier, the epidemiological models have a rich history after Kermack’s original work. There are several excellent and modern text books [6,7,8,9] that describe the fundamental mathematics of epidemiology and discuss the relevance to real historical data of infectious diseases, and we refer the reader to them for a clearer understanding of the model assumptions, derivations and implications. Hethcote’s paper [10] is an especially instructive review and [11] is another that skews toward policy decisions.
In terms of nonlinear dynamics, early work by [12, 13] analyzed the effect of seasonal fluctuations as well as contact rate periodicity in what essentially becomes a forced response problem resulting in harmonic and subharmonic resonances. Several authors have analyzed the occurrence of periodic solutions through Hopf bifurcations in an SEIR model due to the presence of time delays and nonlinear incidence rates [14,15,16,17]. Schwartz and Smith [18] discovered infinite subharmonic bifurcations in a similar seasonally forced model, while [19] analyzed bifurcations in the context of limited hospital resources. Buonomo et al. [20] is a contemporary review summarizing the literature in seasonal dynamics. Chaotic motion has also been documented in [21, 22]. Finally, Martcheva [8] provides a clear exposition of nonlinear dynamic phenomena in her monograph.
We should note that the key parameters that can be quite powerful in estimating—and controlling—the spread of epidemics are the so-called reproduction number (\(R_0\)) and incubation period. In particular, it can be shown even with the simplest models that the disease will persist if \(R_0>1\) and will die out if this number is less than 1. Many of the control techniques that the governments use are focused on achieving this goal by reducing the transmission rate that eventually controls \(R_0\). From the point of view of mathematical analysis, this creates an interesting situation of a time-varying parameter that is usually discontinuous as government polices are often implemented like step functions. It should be noted that the incubation period is characteristic of the virus and is less under our control. It has been estimated to be 6–7 days [23, 24].
As mentioned earlier, COVID-19 has spawned a rich collection of publications, and we do not deem it necessary to document them here. Nevertheless, it is interesting to note the rapid revelations that have come out of these admittedly short-term studies, many of them focusing on data from Wuhan, China, where the virus apparently originated. WHO [25] reports that the earliest infections were identified there around the first of December and the infections declined by the end of February with strong government action as well as public reaction. The crude fatality rate was estimated to be a shockingly high 3.8%, although the real number is in all likelihood much lower since the number of infected individuals is heavily undercounted due to logistical limitations in testing, and given that a significant segment of the population is probably infected but asymptomatic.
In quick studies, several researchers [26,27,28] have estimated the essential epidemiological parameters using early data from Wuhan, China; in particular, they found \(R_0\) to be in the range of 2–3. Liu et al. [29] estimated the reproduction number to be 2.7, which is larger than the earlier SARS epidemic, which would make it more dangerous than SARS. Kucharski et al. [30] estimated that the travel restrictions that the Chinese government imposed brought down \(R_0\) from 2.35 to 1.05, effectively bringing the infections in Wuhan under control. Even more impressive was the effect of aggressive restrictions on the Diamond Princess cruise ship, which was estimated to reduce \(R_0\) from a devastating 14.8 to a more manageable 1.8 [31]. Several papers have been published attempting to estimate the growth in other areas of China and the world. Wu et al. [32] estimated \(R_0\) to be 2.7, and predicted similar transmission rates for other cities in China, and [33], published in mid-March assuming a reproduction number of 2.4, suggested mitigation strategies for various countries, principally US and UK. This last report was quite influential and led to these two governments to start implementing policies with the objective of “flattening the curve” of cumulative infections.
The focus of our study is twofold.
-
We select a dataset for COVID-19 that is reasonably complete and accurate and develop a mathematical model that is best able to represent the data.
-
Given the above fitted model as a starting point, we wish to explore the fundamental nonlinear dynamics of the system and perform a parametric analysis to explore the effect of social dynamics.
The reason we use the actual data (in this case, South Korea’s) is to keep us grounded in reality and to anchor our parametric studies around this particular situation. In addition, we expect that a parametric analysis will show the tremendous implication of various actions on the progression of the disease. In general, our analysis is intended to be relevant to the current situation. Given that, as of the writing of this paper, the COVID-19 situation is still evolving with considerable uncertainty about the future, we wish to use this paper to validate the importance of mathematical modeling in general, and nonlinear dynamic analysis in particular, to enhance our insights.
Building on the above objectives, the rest of the paper is organized as follows. First, we describe the modified SEIR mathematical model we employ in this study. Next, we describe the data collection and properties. Then, we describe a numerical algorithm we employed and coaxed to get the best parametric fits. The next section carries out the nonlinear dynamic analysis and describes the interesting results we have achieved. Finally, we discuss the implications of the model and the results and end with a conclusion.
2 Notes on mathematical models
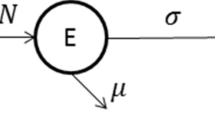
We adopt the susceptible–exposed–infectious–removed (SEIR) framework with a total population size of N. In this model, S, E and I represent the susceptible, exposed and infectious populations and R represents the removed population. For completeness, it is best to start with a standard SEIR model as illustrated in Fig. 1 [6, 8]:
where \('\) denotes derivative with respect to time.
In this model, \(\beta \) is the transmission rate, \(\mu \) is the death (and emigration) rate, \(\sigma \), the incubation rate, is the reciprocal of the latent period (assumed to be the same as the incubation period in this model) and \(\gamma \) is the removal rate, and hence the reciprocal of the recovery period (if removal is due to recovery). Note that E represents those who are exposed but not yet infectious. We make two modifications to the standard model as described below.
The first modification concerns the specific nature of COVID-19 and concerns the fact that infected people can be contagious before they show symptoms during the incubation period. Hence, it is possible that susceptible individuals would have had contact with individuals in both the exposed and infected categories. Here, we will model the two paths from S to E using two values of \(\beta \), say \(\beta _1\) and \(\beta _2\). Emulating [34, 35], we will assume that \(\beta _2 = \beta _1 /2\) or that the probability of contacts with asymptotic infected individuals is half of the probability of contacts with exposed individuals. The modified model now becomes:
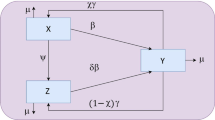
The second modification, illustrated in Fig. 2, concerns the influence of two important sociological (and arguably, political) parameters: social behavior and government policy. Here, we consider the transmission rates to be variable and change with these parameters [36, 37]. Then, the modified model becomes
where we have defined an infection function \(\varUpsilon \) as follows.
Here, \(\alpha \) represents the strength of the government action and \(\kappa \) is the strength of public response. Note that D is a new state variable representing social behavioral dynamics. d represents the strength of public perception of risk, \(1/\lambda \) is the mean period of public response and the model reflects the fact that public reaction would increase when more people get infected and would naturally diminish over time.
3 Parameter identification
3.1 Data
We use the data from South Korea as our dataset for model fitting for several reasons. Compared to USA, where the testing kits are in significant shortage, and China, in particular Wuhan, where the infected cases went up abruptly in a short period and hence massive testing might not have been available, the South Korean government was prepared with appropriate emergency measures since January 20, when it changed its infectious disease alert (in the national crisis management system) category from Level 1 (blue) to Level 2 (yellow) [38]. Such measures provided massive testing capability in South Korea to enable one of the most accurate datasets available.
We examined various databases of South Korea and finally selected COVID-19 Data Repository by the Center for Systems Science and Engineering (CSSE) at Johns Hopkins University [39] due to its complete record and accessible interface. In particular, the database provides time-series data containing daily updates on the new infected cases, death cases and recovered cases, all in a comma-separated values (CSV) file format that is ready to be read and manipulated using standard software tools such as MATLAB.
3.2 Genetic algorithm
Inspired by Charles Darwin’s theory of natural evolution, Holland introduced and popularized general-purpose search algorithms that use principles of natural population genetics to evolve solutions to problems, called genetic algorithms (GA) [40]. The basic idea in GAs is that evolution will choose the fittest species over time. Through emulation of the natural evolution of biological organisms, GA produces a population of individuals (potential solutions in each iteration) to search the solution space of the problem and evolve them through generations to approach the optimal solution. In each generation, the fitness of individuals is evaluated using an objective function and the fittest ones have higher probability to participate in the offspring production process of the next generation. Three main types of operators are employed in GA to guide it toward a solution:
-
Selection to choose between the solutions;
-
Mutation to create and keep genetic diversity; and
-
Crossover to combine the existing solutions into new ones.
Finally, when the stopping criterion is met, the best individual is presented by GA as the solution to the optimization problem.
In this part of the study, the objective is to identify the parameters of the model in such a way that the simulated data match the real data as much as possible and then use the tuned model to analyze and forecast the spread of COVID-19 in the future. The simulated data are obtained by numerically solving the model in Eq. (2) using an integration algorithm (we used sixth-order Runge–Kutta algorithm). To accomplish the first part, namely parameter identification, we use GA to find the parameter values which minimize the cost function between the model prediction and real data. We devise the cost function based on a weighted sum of the mean square error for both infected and removed data. Furthermore, as the main purpose of the model is to predict the future, and as the error at the end of the training time span is reflected significantly on the future time evolution, a penalty factor was included in the cost function for the end points.
The cost function f is hence defined as follows:
where R, I, r, m, s and e stand for removed cases, infected cases, real data, model-predicted data, start date and end date, respectively. Also, \(W_I\) and \(1-W_I\) are, respectively, the infected and removed patient weights, and \(\alpha _\mathrm{p}\) is the penalty factor for the end points. For this part of the study, the model described in Sect. 2 was used with the assumption that \(\mu \) and \(\varLambda \) are zero. The target parameters are \(\beta _1\), \(\beta _2\) and \(\gamma \), while \(\sigma \) was assumed to be 0.14, equivalent to incubation period of 7 days for COVID-19 [41]. We will consider the population to be constant; in other words, we assume that N does not change. This means that the natural mortality (including emigration/immigration) rate (\(\mu \)) and the birth rate (\(\varLambda \)) are zero. This assumption is reasonable over the short time period of analysis.
As explained earlier in this study, factors like government actions can significantly affect the trend and pattern of disease spread and accordingly, the SEIR model parameters. So, in this study, we solved the parameter identification problem for two separate time spans, i.e., controlled and uncontrolled [42].
Totally, the recorded data of 108 days were employed in this study (Jan 22, 2020 to May 8, 2020). The uncontrolled data were taken for first 40 days (Jan 22, 2020 to March 1, 2020) and controlled data for the next 68 days (March 2, 2020 to May 8, 2020). Out of 68 days of controlled time span, first 40 days were used for model tuning and the next 28 days for evaluating the performance of the model in forecasting the unseen data. The total population of South Korea was taken to be 51,269,185 from standard sources.
3.3 Results
The process of optimum selection of the optimization variables was accomplished with a population size of 200 with a crossover probability of 0.8 for 300 generations. For uncontrolled and controlled time spans, the values of \(\alpha _\mathrm{p}\) and \(W_I\) were 10 and 0.5, respectively. \(W_I=0.5\) means that the model-predicted removed and infection rates have the same weights in the cost function and so the optimization algorithm tries to make both of them close to the real data, simultaneously and equally. Also, \(\alpha _\mathrm{p}=10\) means that the square error of model infection and removed rates at each end point has ten times more effect on the cost function than the mean square error of all 40 days and this enforces the model to be close to the real data at the end points. The initial number of infected and removed cases for the SEIR model in both periods was considered as the real data, i.e., \(I_0=1\) and \(R_0=0\) for uncontrolled and \(I_0=3736\) and \(R_0=47\) for controlled time span. Also, due to lack of \(E_0\) (initial number of exposed individuals) in the available dataset, it was assumed to be two times \(I_0\). The trend of optimal tuning of the model parameters for the controlled time spans is shown in Fig. 3. The convergence of the best fitness value range, including best, mean and worst values, to an optimum condition over 300 generations is demonstrated in the logarithmic form in this figure.
The GA parameter identification results are presented in Table 1. As can be seen in this table, the values of model parameters changed significantly with transition from uncontrolled to controlled time span owing to strong actions which were imposed to control the disease transmission in South Korea. The effect of this change in the parameter values is clearly seen in the comparison between the trend of individual numbers in the uncontrolled (Fig. 4) and controlled (Fig. 5) time spans. The sharp drop in the number of active infected individuals and reduction in the growing slope of accumulative removed cases show that the actions that have been taken in this country to control the COVID-19 spread have been quite successful.
Comparison of model and real data for the first 80 days indicates that parameter identification for both uncontrolled and controlled conditions has been performed, appropriately, and there is good agreement between them. Also, it is observed that the model was able to forecast the unseen data of days 81–108 quite well. Nevertheless, there is still a difference between real and model-predicted data. Some possible reasons include perhaps overly simplistic modeling of sociological behavior and government actions and inaccuracy in the assumed model parameters like \(\sigma , E_0, \varLambda \) and \(\mu \). It should also be noted that the number of infected individuals is a measure of the amount of testing that was done, which has not been comprehensive, and hence the numbers can be inaccurate. For all these reasons, the fluctuations seen in the real data are not predicted precisely by the model, but it is clear that the general trends of variation in both infection and removed rates are quite similar.
4 Nonlinear analysis
This section focuses on the disease extinction or persistence, which is determined by the stability of the disease-free equilibrium and the existence of endemic equilibrium. Prevention and control of COVID-19 epidemics require a better understanding of its mode of dissemination as well as the impacts of control strategies. The analysis considers a naïve scenario where there is no governmental action, which is unlikely but will provide a baseline to appreciate the effects of the action. In the second and third scenarios, we consider the effects of individual reaction and the governmental action.
4.1 System without controlling action
In this scenario, the infection function is given by
which captures the possibilities of new infection by both infected and exposed individuals. The corresponding model is shown in Eq. (2).
Proposition 1
The disease-free equilibrium \(E^0=(\varLambda /\mu ,0,0,0)\) of model Eq. (2) is asymptotically stable if \(R_0<1\). The endemic equilibrium \(E^1=(S_0,E_0,I_0,R_0)\) is asymptotically stable if \(R_0>1\) and is defined as:
and
Proof
In order to compute the expression of the equilibrium points, we set the time derivative to zero (steady state) and solve the corresponding algebraic equation.
It is obvious that \(E^0(\varLambda /\mu ,0,0,0)\) is a trivial solution of Eq. (9). \(E^0\) is called the disease-free equilibrium since it is obtained for \(I=E=0\) and the corresponding infected function \(\varUpsilon \) is zero. For \(I\ne 0\), the model in Eq. (2) has a nonzero solution \(E^1\) given by Eq. (7).
The stability of the equilibrium points \(E^0\) and \(E^1\) is obtained from the Routh–Hurwitz criterion for stability, which states that the equilibrium state is stable if the roots of the characteristic polynomial in \(\zeta \) are all negative. The Jacobian matrix of the system is obtained as
with
The characteristic polynomial for the DFE is the following (\(E_0=I_0=0\) and \(S_0=\varLambda /\mu \))
with
The system is stable if the roots of the characteristic equation Eq. (11) are all negative; this is satisfied if \(R_0<1\), which is equivalent to
For the endemic equilibrium, the steady-state system in Eq. (9) can be solved to obtain Eq. (7). The coefficients of the characteristic polynomial are given as
The system is stable if the roots of the characteristic polynomial are all negative, that is, if \(R_0>1\), which is equivalent to
Figure 6a shows an illustration of a DFE situation where \(R_0=0.7\) and \(\beta _2=0.0517, \beta _1=0.0024, \sigma =0.14\) and \(\gamma =0.0026\). Using the transmission rate coefficients obtained from Sect. 3 (\(\beta _2=0.0628, \beta _1=0.407\)), we get the endemic equilibrium of Fig. 6b. The effects of the transmission rates \(\beta _1\) and \(\beta _2\) are illustrated in Fig. 7. The figure considers the situation of fewer contacts with infected individuals (\(\beta _1<\beta _2\), most/some infected individual are in quarantine assuming the same probability of contamination once in close contact) and compares it to the situation where we have higher probability of contamination with infected individuals, or \(\beta _1>\beta _2\)). Beyond \(R_0=1\), the proportion of infected individuals naturally increases and is higher when \(\beta _2>\beta _1\). This can be interpreted to mean that exposed people will have a greater impact on the persistence of the disease. The results of Fig. 7 confirm the observations of the number of newly confirmed cases due to close contact with exposed and infected individuals in Wuhan, China [35].
4.2 Effects of governmental action
In the context of COVID-19, governmental actions are mainly focused on regulating social life to reduce the likelihood of contact between individuals. This naturally impacts the transmission rates. The effects of governmental actions are summarized in the infection function, which would need to be substituted into Eq. (3); however, note that we do not consider the effect of public reaction here; hence, we drop D from the equation.
Proposition 2
In this case, an endemic equilibrium (\(R_0>1\)) is persistent if
Proof
Under the effect of governmental action, repeating the analysis in the previous paragraph will not change the DFE, endemic equilibrium and the stability conditions if \(\beta _i\) is replaced by \((1-\alpha )\beta _i\), (\(i=1,2\)). However, the reproduction number becomes
The endemic equilibrium is stable if \(R_{00}>1\), which leads to the critical value of the governmental control
Effects of the governmental control on the endemic equilibrium for the values of Fig. 6. a Effects of \(\alpha \) on the reproduction number for \(\beta _1=4\beta _2\). b Effects of \(\alpha \) on the proportion of infected individuals for \(R_0>1\) computed from the equation
Figure 8 gives two different views of how the government action could contribute to controlling the spread of the disease. As might be expected, stronger governmental action (higher values of \(\alpha \)) has more impact on the disease (Fig. 8a). But, what is more interesting is that the results predict the existence of a threshold value \(\alpha _c\) expressed as a function of the transmission rate that would lead to complete control of the disease. This threshold value is higher for lager values of \(\beta _2\). In practice of course, there would be a natural limit to the governmental action. For this reason, additional controls would be needed. The literature that documents past infectious diseases similar to the COVID-19 has shown how an increase in the number of deaths and the severity of critical cases can be leveraged to impact the perception and seriousness of the population.
4.3 System with additional control
We now take into consideration the combined effects of the government action and the public perception of risk regarding the number of severe and critical cases. The variable D is added to the model to represent the public perception of risk. It increases when people die and will decay naturally, meaning that perception of risk diminishes over time in the absence of the COVID-19. The intensity of this perception is carried through the intensity of the population response \(\kappa \) and proportion of severe cases d. The infection function is now
which would be substituted into the model given by Eq. (3).
Proposition 3
The system in Eq. (3) under control has a higher threshold for the onset of endemic equilibrium. This onset value is \(R_0=1\) for \(\kappa =0\) and \(R_0>1+\kappa _{\mathrm {effect}}\) for large values of \(\kappa \), where
Proposition 4
There is an endemic state for which the intensity of the public perception has no effect. That endemic state is defined by:
Proof
The steady-state conditions lead to
where the subscript c stands for control.
The transcendental equation would not lead to an explicit expression of \(I_{c0}\). Thus, guided by the literature, we limit the analysis to some specific cases:
For \( \kappa ~~\rightarrow ~~\infty \)
if \(R_0-1>\frac{\beta _1\sigma }{\beta _2(\gamma +\mu )}\)
For other values of \(\kappa \), it can be shown that a single \(0<I_{c0}^*\) exists if
This can be proven graphically as shown in “Appendix.”
Figure 9 shows how the intensity of the population response could impact the spread of the disease. In fact, under this control, the number of infections is considerably reduced as shown in the figures. In Fig. 9a, there is a jump in the number of infected for small \(R_0\). This jump is significant for smaller value of \(\kappa \) and is likely a manifestation of the nonlinearity in \(\kappa \) in the expression of the infection function. Recalling that the endemic equilibrium used here was obtained for \(\kappa \rightarrow \infty \), the results of Fig. 9a are only valid for larger values of \(\kappa \). This nonlinearity is not visible in the presence of \(\alpha \) as shown in Fig. 9b.
Figure 10 shows an illustration of the system response for a naïve scenario where there is no governmental action (Fig. 10a), the effects of governmental action alone (Fig. 10b), individual reaction alone (Fig. 10c) and combined action (Fig. 10d). Simulation and analytical derivation show that carefully setting the parameters (in the specified range of vales) could effectively stop the spread of the disease under combined actions.
5 Summary of findings
We summarize below the key findings of our analysis.
-
The reproduction number, traditionally computed for SEIR model in terms of \(\sigma ,\varLambda ,\mu \) and \(\gamma \), has been expanded to include \(\beta _1, \beta _2\), and the social and policy parameters, \(\alpha \) and \(\kappa \). This expanded definition embeds social dynamics neatly into the epidemiological model and significantly expands insight into their interactions.
-
The parameter values for transmissibility (\(\beta _1, \beta _2\)) and hence the reproduction number (\(R_0\)) went through significant reduction with the South Korean government response roughly 40 days after the first incidence.
-
Exposed people (as opposed to infected individuals) have a greater impact on the persistence of the disease.
-
The stronger the government action, the more the impact on disease transmission.
-
There is a minimum threshold value for government action (\(\alpha _c\)) for complete control of the disease. Our model predicts that numerous small, tentative steps would not be as effective as bolder and significant steps.
-
The intensity of the public response (\(\kappa \)) has significant impact on the reduction in number of infections.
-
The model predicts that for some values of the disease dynamics, the public perception \(\kappa \) will have no effects. In this case, only the governmental action could stop the spread of the disease.
-
The analysis predicts that a suitable combination of government response (\(\alpha \)) and public reaction (\(\kappa \)) would effectively stop pandemics such as COVID-19.
6 Conclusion
In this paper, we adapted and developed an SEIR model for the COVID-19 pandemic including different transmission rates for contacts with infected and exposed and integrated parameters and variables to model government action and social reaction. First, we used data from South Korea to perform a parametric analysis using the genetic algorithm and achieved a very good fit. This provides sound validation for our model. The resulting numerical analysis shows that the South Korean government action 40 days after the infection was first diagnosed had a significant influence on the spreading of the disease.
Next, we used more nuanced models for nonlinear dynamic analysis. Equilibrium and stability analysis was performed revealing several areas of the parameter space where a stable endemic equilibrium can exist leading to persistent infections. We considered three situations: (a) without control, (b) with government action and (c) with combined effect of government action and public reaction. Results show that it is possible to stop the spread of the disease (or to extinguish the endemic equilibrium) by proper choice of parameters that govern social and government behavior.
In this paper, by seamlessly integrating two important sociological (and arguably, political) parameters, i.e., public perception and government policy, we are able to show the fact that these factors can significantly affect the transmission rate and spread pattern of disease evolution. The conclusions would support an argument that stronger government actions and policies such as quarantine, wearing masks, social distancing and improving public perception might be essential in combating the COVID-19 spread. Indeed, this is demonstrated in South Korea, which has arguably achieved tremendous success in combating COVID-19 unlike many other countries. Similar perspectives should be considered for further government policy regarding progressively reopening the economy and campuses. A potential future direction is to integrate more aspects including seasonal effects, which would likely lead to periodic responses.
Finally, as we write this paper, we note that the pandemic situation is still evolving with considerable uncertainty about the future. We believe that this paper demonstrates the importance of nonlinear dynamic analysis to enhance our understanding of the natural world in which we the humans live and has profound implications for the way we handle it in the future.
References
Bernoulli, D.: Essai d’une nouvelle analyse de la mortalite causee par la petite verole. Mem. Math. Phys. Acad. R. Sci. (1766)
Dietz, K., Heesterbeek, J.: Daniel Bernoulli’s epidemiological model revisited. Math. Biosci. 180(1), 1–21 (2002)
Kermack, W.O., McKendrick, A.G., Walker, G.T.: A contribution to the mathematical theory of epidemics. Proc. R. Soc. Lond. 115(772), 700–721 (1927)
Kermack, W.O., McKendrick, A.G.: Contributions to the mathematical theory of epidemics—II. The problem of endemicity. Bull. Math. Biol. 53, 57–87 (1932)
Kermack, W.O., McKendrick, A.G.: Contributions to the mathematical theory of epidemics—III. Further studies of the problem of endemicity. Bull. Math. Biol. 53, 89–118 (1933)
Keeling, M.J., Rohani, P.: Modeling Infectious Diseases in Humans and Animals. Princeton University Press, Princeton (2008)
Brauer, F.: Mathematical Models in Epidemiology. Springer, Berlin (2019)
Martcheva, M.: An Introduction to Mathematical Epidemiology, 1st edn. Springer, Berlin (2015)
Vynnycky, E., White, R.G.: An Introduction to Infectious Disease Modelling. Oxford University Press, Oxford (2010)
Hethcote, H.W.: The mathematics of infectious diseases. SIAM Rev. 42(4), 599–653 (2000)
Heesterbeek, H., Anderson, R.M., Andreasen, V., Bansal, S., De Angelis, D., Dye, C., Eames, K.T.D., Edmunds, W.J., Frost, S.D.W., Funk, S., Hollingsworth, T.D., House, T., Isham, V., Klepac, P., Lessler, J., Lloyd-Smith, J.O., Metcalf, C.J.E., Mollison, D., Pellis, L., Pulliam, J.R.C., Roberts, M.G., Viboud, C.: Modeling infectious disease dynamics in the complex landscape of global health. Science (New York, N.Y.) 347, aaa4339 (2015)
Grossman, Z., Gumowski, I., Dietz, K.: The incidence of infectious diseases under the influence of seasonal fluctuations–analytical approach. In: Lakshmikantham, V. (ed.) Nonlinear Systems and Applications, pp. 525–546. Academic Press, London (1977)
Grossman, Z.: Oscillatory phenomena in a model of infectious diseases. Theor. Popul. Biol. 18(2), 204–243 (1980)
Hethcote, H.W., Stech, H.W., Van Den Driessche, P.: Nonlinear oscillations in epidemic models. SIAM J. Appl. Math. 40(1), 1–9 (1981)
Hethcote, H.W., van den Driessche, P.: Some epidemiological models with nonlinear incidence. J. Math. Biol. 29(3), 271–287 (1991)
Bauch, C.T., Earn, D.J.D.: Transients and attractors in epidemics. Proc. Biol. Sci. 270, 1573–1578 (2003)
Abta, A., Laarabi, H., Talibi Alaoui, H.: The Hopf bifurcation analysis and optimal control of a delayed SIR epidemic model. Int. J. Anal. 2014, 940819 (2014)
Schwartz, I.B., Smith, H.L.: Infinite subharmonic bifurcation in an SEIR epidemic model. J. Math. Biol. 18(3), 233–253 (1983)
Yan, C., Jia, J.: Hopf bifurcation of a delayed epidemic model with information variable and limited medical resources. Abstr. Appl. Anal. 2014, 109372 (2014)
Buonomo, B., Chitnis, N., D’Onofrio, A.: Seasonality in epidemic models: a literature review. Ricerche Mat. 67(1), 7–25 (2018)
Olsen, L.F., Truty, G.L., Schaffer, W.M.: Oscillations and chaos in epidemics: a nonlinear dynamic study of six childhood diseases in copenhagen. Denmark. Theor. Popul. Biol. 33, 344–70 (1988)
Earn, D.J., Rohani, P., Grenfell, B.T.: Persistence, chaos and synchrony in ecology and epidemiology. Proc. Biol. Sci. 265, 7–10 (1998)
Tang, B., Wang, X., Li, Q., Bragazzi, N.L., Tang, S., Xiao, Y., Wu, J.: Estimation of the transmission risk of the 2019-nCOV and its implication for public health interventions. J. Clin. Med. 9, 462 (2020)
Backer, J.A., Klinkenberg, D., Wallinga, J.: Incubation period of 2019 novel coronavirus (2019-nCOV) infections among travellers from Wuhan, China, 20–28 January 2020. Eurosurveillance 25, 2000062 (2020)
Mission, T.W.-C.J.: Report of the WHO-China joint mission on coronavirus disease 2019 (COVID-19). World Health Organization, Technical Report (2020)
Read, J.M., Bridgen, J.R., Cummings, D.A., Ho, A., Jewell, C.P.: Novel coronavirus 2019-nCOV: early estimation of epidemiological parameters and epidemic predictions. medRxiv [Online]. Available: https://www.medrxiv.org/content/early/2020/01/28/2020.01.23.20018549 (2020)
Liu, T., Hu, J., Xiao, J., He, G., Kang, M., Rong, Z., Lin, L., Zhong, H., Huang, Q., Deng, A., Zeng, W., Tan, X., Zeng, S., Zhu, Z., Li, J., Gong, D., Wan, D., Chen, S., Guo, L., Li, Y., Sun, L., Liang, W., Song, T., He, J., Ma, W.: Time-varying transmission dynamics of novel coronavirus pneumonia in China. bioRxiv [Online]. Available: https://www.biorxiv.org/content/early/2020/02/13/2020.01.25.919787 (2020)
Li, Q., Guan, X., Wu, P., Wang, X., Zhou, L., Tong, Y., Ren, R., Leung, K.S., Lau, E.H., Wong, J.Y., Xing, X., Xiang, N., Wu, Y., Li, C., Chen, Q., Li, D., Liu, T., Zhao, J., Liu, M., Tu, W., Chen, C., Jin, L., Yang, R., Wang, Q., Zhou, S., Wang, R., Liu, H., Luo, Y., Liu, Y., Shao, G., Li, H., Tao, Z., Yang, Y., Deng, Z., Liu, B., Ma, Z., Zhang, Y., Shi, G., Lam, T.T., Wu, J.T., Gao, G.F., Cowling, B.J., Yang, B., Leung, G.M., Feng, Z.: Early transmission dynamics in Wuhan, China, of novel coronavirus-infected pneumonia. N. Engl. J. Med. 382(13), 1199–1207 (2020)
Liu, Y., Gayle, A.A., Wilder-Smith, A., Rocklöv, J.: The reproductive number of COVID-19 is higher compared to SARS coronavirus. J. Travel. Med. (2020). https://doi.org/10.1093/jtm/taaa021
Kucharski, A.J., Russell, T.W., Diamond, C., Liu, Y., Edmunds, J., Funk, S., Eggo, R.M.: Early dynamics of transmission and control of COVID-19: a mathematical modelling study. Lancet Infect. Dis. 20(5), 553–558 (2020)
Rocklöv, J., Sjödin, H., Wilder-Smith, A.: COVID-19 outbreak on the Diamond Princess cruise ship: estimating the epidemic potential and effectiveness of public health countermeasures. J. Travel. Med. (2020). https://doi.org/10.1093/jtm/taaa030
Wu, J.T., Leung, K., Leung, G.M.: Nowcasting and forecasting the potential domestic and international spread of the 2019-nCOV outbreak originating in Wuhan, China: a modelling study. The Lancet 395(10225), 689–697 (2020)
Ferguson, N.M., Laydon, D., Nedjati-Gilani, G., Imai, N., Ainslie, K., Baguelin, M., Bhatia, S., Boonyasiri, A., Cucunubá, Z., Cuomo-Dannenburg, G., Dighe, A., Dorigatti, I., Fu, H., Gaythorpe, K., Green, W., Hamlet, A., Hinsley, W., Okell, L.C., van Elsland, S., Thompson, H., Verity, R., Volz, E., Wang, H., Wang, Y., Walker, P.G., Winskill, P., Whittaker, C., Donnelly, C.A., Riley, S., Ghani, A.C.: Impact of non-pharmaceutical interventions (NPIs) to reduce COVID-19 mortality and healthcare demand. Imperial College London, Technical Report (2020)
Gong, J., Sun, Z.L., Li, X.W.: Simulation and analysis of control of severe acute respiratory syndrome. J. Remote Sens. 7, 260–265 (2003)
Hou, C., Chen, J., Zhou, Y., Hua, L., Yuan, J., He, S., Guo, Y., Zhang, S., Jia, Q., Zhao, C., Zhang, J., Xu, G., Jia, E.: The effectiveness of quarantine of Wuhan city against the corona virus disease 2019 (COVID-19): a well-mixed SEIR model analysis. J. Med. Virol. 92, 841–848 (2020)
Lin, Q., Zhao, S., Gao, D., Lou, Y., Yang, S., Musa, S.S., Wang, M.H., Cai, Y., Wang, W., Yang, L., He, D.: A conceptual model for the coronavirus disease 2019 (COVID-19) outbreak in Wuhan, China with individual reaction and governmental action. Int. J. Infect. Dis. 93, 211–216 (2020)
He, D., Dushoff, J., Day, T., Ma, J., Earn, D.J.D.: Inferring the causes of the three waves of the 1918 influenza pandemic in England and Wales. Proc. Biol. Sci. 280, 20131345 (2013)
A timeline of South Korea’s response to COVID-19. [Online]. Available: https://www.csis.org/analysis/timeline-south-koreas-response-covid-19
XXXX
Holland, J.H.: Adaptation in Natural and Artificial Systems. The MIT Press, London (1975)
Tang, Z., Li, X., Li, H.: Prediction of new coronavirus infection based on a modified SEIR model. medRxiv (2020)
De Castro, C.A.: SIR model for COVID-19 calibrated with existing data and projected for Colombia. arXiv preprint arXiv:2003.11230 (2020)
Acknowledgements
CN and FN gratefully acknowledge the financial support from US Office of Naval Research (Grant No. N00014-19-1-2070) for basic research on adaptive modeling of nonlinear dynamic systems. In particular, we appreciate the continuous encouragement from Capt. Lynn Petersen and are humbled by his recognition of the value of our research.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix
Appendix
The existence of a unique endemic value of \(I_{c0}^*\) for
can be shown graphically for all values of \(\kappa \) by plotting the following graphs
with \(X\equiv I_{c0}^*, m=\frac{d\gamma }{\lambda }\) and \(N=\frac{\beta _1\sigma }{\beta _2(\gamma +\mu )}\) The intersection point of Z(X) and Y(X) in the interval [0, 1] will exist if
Figure 11 shows the plot of Z(X) (in black line) and Y(X) for several values of \(\kappa \) from \(\kappa =0\) (no perception) to realistic values of \(\kappa \)x [36]. In all cases, the intersection of Z(X) and Y(X) is singular; thus, there exists a unique \(I_{c0}^*\) solution of Eq. (28).
Rights and permissions
About this article
Cite this article
Kwuimy, C.A.K., Nazari, F., Jiao, X. et al. Nonlinear dynamic analysis of an epidemiological model for COVID-19 including public behavior and government action. Nonlinear Dyn 101, 1545–1559 (2020). https://doi.org/10.1007/s11071-020-05815-z
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11071-020-05815-z