Skip to main content
SpringerLink
Log in

Large deflections of a structurally damped panel in a subsonic flow

  • Original paper
  • Published:
Nonlinear Dynamics Aims and scope Submit manuscript

Abstract

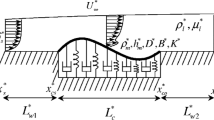
The large deflections of panels in subsonic flow are considered, specifically a fully clamped von Karman plate accounting for both rotational inertia in plate filaments and (mild) structural damping. The panel is taken to be embedded in the boundary of the positive half-space in \(\mathbb R^3\) containing a linear, subsonic potential flow. Solutions are constructed via a semigroup approach despite the lack of natural dissipativity associated with the generator of the linear dynamics. The flow–plate dynamics are then reduced—via an explicit Neumann-to-Dirichlet (downwash-to-pressure) solver for the flow—to a memory-type dynamical system for the plate. For the non-conservative plate dynamics, a global attractor is explicitly constructed via Lyapunov and recent quasi-stability methods. Finally, it is shown that, via the compactness of the attractor and finiteness of the dissipation integral, all trajectories converge strongly to the set of stationary states.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

Notes

  1. If \(\varOmega \) is a rectangle, no results below are affected.

  2. The perturbation \(\mu >0\) is introduced to dispense with the zero eigenvalue; later that this will be taken as a bounded perturbation on Y and removed to obtain the problem as originally stated.

  3. Without loss of generality, take \(t_0=0\).

  4. Barbalat’s Lemma : Suppose \(f(t) \in C^1(a, \infty )\) and \(\displaystyle \lim _{t\rightarrow \infty } f(t) =\alpha < \infty .\) If \(f'(t)\) is uniformly continuous, then \(\displaystyle \lim _{t\rightarrow \infty } f'(t) = 0.\) In our case, we take \(f(t)=\int _0^{t}\Big |(M_{\alpha }u_t,w)\Big |^2\mathrm{d}\tau \).

References

  1. Babin, A., Vishik, M.: Attractors of Evolution Equations. North-Holland, Amsterdam (1992)

    MATH  Google Scholar 

  2. Balakrishnan, A.V.: Aeroelasticity—Continuum Theory. Springer, Berlin (2012)

    Book  Google Scholar 

  3. Bolotin, V.V.: Nonconservative Problems of Elastic Stability. Pergamon Press, Oxford (1963)

    MATH  Google Scholar 

  4. Boutet de Monvel, L., Chueshov, I.: Non-linear oscillations of a plate in a flow of gas. C. R. Acad. Sci. Paris Ser. I 322, 1001–1006 (1996)

    MathSciNet  MATH  Google Scholar 

  5. Boutet de Monvel, L., Chueshov, I.: Oscillation of von Karman’s plate in a potential flow of gas Izvestiya RAN. Ser. Mat. 63, 219–244 (1999)

    MATH  Google Scholar 

  6. Boutet de Monvel, L., Chueshov, I., Rezounenko, A.: Long-time behaviour of strong solutions of retarded nonlinear PDEs. Commun. PDEs 22, 1453–1474 (1997)

    Article  Google Scholar 

  7. Chueshov, I.: Dynamics of Quasi-Stable Dissipative Systems. Springer, Berlin (2015)

    Book  Google Scholar 

  8. Chueshov, I.: On a certain system of equations with delay, occurring in aeroelasticity. Teor. Funktsii Funktsional. Anal. i Prilozhen, 54, 123–130 (1990) (in Russian); translation in J. Soviet Math., 58, 385–390 (1992)

  9. Chueshov, I.: Dynamics of von Karman plate in a potential flow of gas: rigorous results and unsolved problems. In: Proceedings of the 16th IMACS World Congress, Lausanne, Switzerland, pp. 1–6 (2000)

  10. Chueshov, I., Dowell, E., Lasiecka, I., Webster, J.T.: Nonlinear elastic plate in a flow of gas: recent results and conjectures. Appl. Math. Optim. 73(3), 475–500 (2016)

    Article  MathSciNet  Google Scholar 

  11. Chueshov, I., Dowell, E., Lasiecka, I., Webster, J.T.: Mathematical aeroelasticity: a survey. J. Math. Eng. Sci. Aerosp. 7(1), 1–26 (2016)

    Google Scholar 

  12. Chueshov, I., Lasiecka, I.: Long-time behavior of second-order evolutions with nonlinear damping. Mem AMS 195 (2008)

  13. Chueshov, I., Lasiecka, I.: Von Karman Evolution Equations, Well-Posedness and Long-Time Behavior Monographs. Springer, Berlin (2010)

    MATH  Google Scholar 

  14. Chueshov, I., Lasiecka, I.: Generation of a semigroup and hidden regularity in nonlinear subsonic flow-structure interactions with absorbing boundary conditions. J. Abstr. Differ. Equ. Appl. 3, 1–27 (2012)

    MathSciNet  MATH  Google Scholar 

  15. Chueshov, I., Lasiecka, I., Webster, J.T.: Attractors for delayed, non-rotational von Karman plates with applications to flow-structure interactions without any damping. Commun. PDE 39(11), 1965–1997 (2014)

    Article  Google Scholar 

  16. Chueshov, I., Lasiecka, I.: JT webster evolution semigroups for supersonic flow-plate interactions. J. Differ. Eqs. 254, 1741–1773 (2013)

    Article  Google Scholar 

  17. Ciarlet, P., Rabier, P.: Les Equations de Von Karman. Springer, Berlin (1980)

    Book  Google Scholar 

  18. de Monvel, A.B., Chueshov, I.: The problem of interaction of von Karman plate with subsonic flow gas. Math. Methods Appl. Sci. 22, 801–810 (1999)

    Article  MathSciNet  Google Scholar 

  19. Dowell, E.: Nonlinear oscillations of a fluttering plate, I and II. AIAA J., 4(1966), 1267–1275; and 5, 1857–1862 (1967)

  20. Dowell, E.: Panel flutter—a review of the aeroelastic stability of plates and shells. AIAA J. 8, 385–399 (1970)

    Article  Google Scholar 

  21. Dowell, E.: A Modern Course in Aeroelasticity. Kluwer Academic Publishers, Berlin (2004)

    MATH  Google Scholar 

  22. Dowell, E.H.: Some recent advances in nonlinear aeroelasticity: fluid-structure interaction in the 21st century. In: Proceedings of the 51st AIAA/ASME/ASCE/AHS/ASC Structures. AIAA, p. 3137 (2010)

  23. Dowell, E.H.: Flutter of a buckled plate as an example of chaotic motion of a deterministic autonomous system. J. Sound Vib. 85(3), 333–344 (1982)

    Article  MathSciNet  Google Scholar 

  24. Howell, J., Huneycutt, K., Webster, J.T., Wilder, S.: Stability of thin beams in a potential flow. Math. Eng. 1(3), 614–647 (2019)

    Article  MathSciNet  Google Scholar 

  25. Holmes, P., Marsden, J.: Bifurcation to divergence and flutter in flow-induced oscillations: an infinite dimensional analysis. Automatica 14(4), 367–384 (1978)

    Article  MathSciNet  Google Scholar 

  26. Kukavica, I., Lasiecka, I., Triggiani, R., Tuffaha, A.: Webster JT : Mathematical Theory of Evolutionary Fluid-Flow Structure Interactions. Springer, Berlin (2018)

    MATH  Google Scholar 

  27. Lagnese, J.: Boundary Stabilization of Thin Plates. SIAM, University City (1989)

    Book  Google Scholar 

  28. Lasiecka, I., Triggiani, R.: Control Theory for Partial Differential Equations: vol. 1. Continuous and Approximation Theories, Abstract Parabolic Systems. Cambridge University Press, Cambridge (2000)

    Book  Google Scholar 

  29. Lasiecka, I., Webster, J.T.: Generation of bounded semigroups in nonlinear flow-structure interactions with boundary damping. Math. Methods Appl. Sci. (2011). https://doi.org/10.1002/mma.1518

    Article  MATH  Google Scholar 

  30. Lasiecka, I., Webster, J.T.: Eliminating flutter for clamped von Karman plates immersed in subsonic flows. Commun. Pure Appl. Anal. 13(5), 1935–1965 (2014)

    Article  MathSciNet  Google Scholar 

  31. Lasiecka, I., Webster, J.T.: Feedback stabilization of a fluttering panel in an inviscid subsonic potential flow. SIAM J. Math. Anal. 48(3), 1848–1891 (2016)

    Article  MathSciNet  Google Scholar 

  32. Miyatake, S.: Mixed problem for hyperbolic equation of second order. J. Math. Kyoto Univ. 13, 435–487 (1973)

    MathSciNet  MATH  Google Scholar 

  33. Pazy, A.: Semigroups of Linear Operators and Applications to Partial Differential Equations, vol. 44. Springer, Berlin (2012)

    MATH  Google Scholar 

  34. Ryzhkova, I.: Stabilization of a von Karman plate in the presence of thermal effects in a subsonic potential flow of gas. J. Math. Anal. Appl. 294, 462–481 (2004)

    Article  MathSciNet  Google Scholar 

  35. Ryzhkova, I.: Dynamics of a thermoelastic von Karman plate in a subsonic gas flow. Z. Angew. Math. Phys. 58, 246–261 (2007)

    Article  MathSciNet  Google Scholar 

  36. Tataru, D.: On the regularity of boundary traces for the wave equation. Ann. Scuola Normale. Sup. Pisa 26, 185–206 (1998)

    MathSciNet  MATH  Google Scholar 

  37. Temam, R.: Infinite Dimensional Dynamical Systems in Mechanics and Physics. Springer, Berlin (1988)

    Book  Google Scholar 

  38. Webster, J.T.: Weak and strong solutions of a nonlinear subsonic flow-structure interaction: semigroup approach. Nonlinear Anal. 74, 3123–3136 (2011)

    Article  MathSciNet  Google Scholar 

  39. Webster, J.T.: Attractors and determining functionals for a flutter model: finite dimensionality out of thin air. Pure Appl. Funct. Anal. 5(1), 85–119 (2019)

    MathSciNet  MATH  Google Scholar 

Download references

Acknowledgements

The authors would like thank the referees for their critical reading and thoughtful criticisms and suggestions which greatly helped improve the quality of the manuscript. The second author would like to thank the National Science Foundation for its generous support.

Funding

Justin T. Webster would like to thank the National Science Foundation and acknowledge his partial funding from NSF Grant DMS-1907620.

Author information

Authors and Affiliations

  1. University of Maryland, Baltimore county, Baltimore, MD, USA

    Abhishek Balakrishna & Justin T. Webster

Authors
  1. Abhishek Balakrishna
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Justin T. Webster
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Abhishek Balakrishna.

Ethics declarations

Conflict of interest

The authors declare that they have no conflict of interest.

Availability of data and material

Not applicable.

Code availability

Not applicable.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Balakrishna, A., Webster, J.T. Large deflections of a structurally damped panel in a subsonic flow. Nonlinear Dyn 103, 3165–3186 (2021). https://doi.org/10.1007/s11071-020-05805-1

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11071-020-05805-1

Keywords

Mathematics Subject Classification

Search

Navigation