Soliton elastic interactions and dynamical analysis of a reduced integrable nonlinear Schrödinger system on a triangular-lattice ribbon

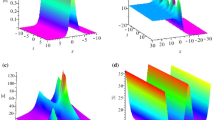
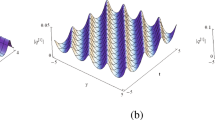
Abstract

Under investigation in this paper is a discrete reduced integrable nonlinear Schrödinger system on a triangular-lattice ribbon, which may have some prospective applications in modern nanoribbon. First, we construct the infinitely many conservation laws and discrete N-fold Darboux transformation for this system based on its known Lax pair. Then bright–bright multi-soliton and breather solutions in terms of determinants are obtained by means of the resulting Darboux transformation. Moreover, we investigate soliton interactions through asymptotic analysis and analyze some important physical quantities such as amplitudes, wave numbers, wave widths, velocities, energies and initial phases. Finally, the dynamical evolution behaviors are discussed via numerical simulations. It is found that soliton interactions in this system are elastic, and their evolutions are stable against a small noise in a short period of time. Results obtained in this paper may have some prospective applications for understanding some physical phenomena.

Appendices

Appendix A

In this Appendix, we give the determinant form of $\Delta a^{(0)}_{n}$, $\Delta b^{(1)}_{n}$, $\Delta b^{(3)}_{n}$ and $\Delta _n$ in two-soliton and two-breather. The detail is as follows:

$$\begin{aligned} \begin{aligned} \Delta _n&=\left| \begin{array}{cccc} z_{1}^2 \phi _{1,n} &{}\phi _{1,n} &{}z_{1}^3 \psi _{1,n} &{}z_{1} \psi _{1,n} \\ z_{2}^2 \phi _{2,n} &{}\phi _{2,n} &{}z_{2}^3 \psi _{2,n} &{}z_{2} \psi _{2,n} \\ z_{1}^{*2} \psi ^*_{1,n} &{}z_{1}^{*4} \psi ^*_{1,n} &{}-z^*_{1} \phi ^*_{1,n} &{}-z_{1}^{*3} \phi ^*_{1,n} \\ z_{2}^{*2} \psi ^*_{2,n} &{}z_{2}^{*4} \psi ^*_{2,n} &{}-z^*_{2} \phi ^*_{2,n} &{}-z_{2}^{*3} \phi ^*_{2,n} \end{array} \right| ,\\ \Delta a^{(0)}_{n}&=\left| \begin{array}{cccc} z_{1}^2 \phi _{1,n} &{}-z_{1}^4 \phi _{1,n} &{}z_{1}^3 \psi _{1,n} &{}z_{1} \psi _{1,n} \\ z_{2}^2 \phi _{2,n} &{}-z_{2}^4 \phi _{2,n} &{}z_{2}^3 \psi _{2,n} &{}z_{2} \psi _{2,n} \\ z_{1}^{*2} \psi ^*_{1,n} &{}-\psi ^*_{1,n} &{}-z^*_{1} \phi ^*_{1,n} &{}-z_{1}^{*3} \phi ^*_{1,n} \\ z_{2}^{*2} \psi ^*_{2,n} &{}-\psi ^*_{2,n} &{}-z^*_{2} \phi ^*_{2,n} &{}-z_{2}^{*3} \phi ^*_{2,n} \end{array} \right| , \\ \Delta b^{(1)}_{n}&=\left| \begin{array}{cccc} z_{1}^2 \phi _{1,n} &{}\phi _{1,n} &{}z_{1}^3 \psi _{1,n} &{}-z_{1}^4 \phi _{1,n} \\ z_{2}^2 \phi _{2,n} &{}\phi _{2,n} &{}z_{2}^3 \psi _{2,n} &{}-z_{2}^4 \phi _{2,n} \\ z_{1}^{*2} \psi ^*_{1,n} &{}z_{1}^{*4} \psi ^*_{1,n} &{}-z^*_{1} \phi ^*_{1,n} &{}-\psi ^*_{1,n} \\ z_{2}^{*2} \psi ^*_{2,n} &{}z_{2}^{*4} \psi ^*_{2,n} &{}-z^*_{2} \phi ^*_{2,n} &{}-\psi ^*_{2,n} \end{array} \right| ,\\ \Delta b^{(3)}_{n}&=\left| \begin{array}{cccc} z_{1}^2 \phi _{1,n} &{}\phi _{1,n} &{}-z_{1}^4 \phi _{1,n} &{}z_{1} \psi _{1,n} \\ z_{2}^2 \phi _{2,n} &{}\phi _{2,n} &{}-z_{2}^4 \phi _{2,n} &{}z_{2} \psi _{2,n} \\ z_{1}^{*2} \psi ^*_{1,n} &{}z_{1}^{*4} \psi ^*_{1,n} &{}-\psi ^*_{1,n} &{}-z_{1}^{*3} \phi ^*_{1,n} \\ z_{2}^{*2} \psi ^*_{2,n} &{}z_{2}^{*4} \psi ^*_{2,n} &{}-\psi ^*_{2,n} &{}-z_{2}^{*3} \phi ^*_{2,n} \end{array} \right| . \end{aligned} \end{aligned}$$

Appendix B

In this Appendix, we give the determinant form of $\Delta a^{(0)}_{n}$, $\Delta b^{(1)}_{n}$, $\Delta b^{(5)}_{n}$ and $\Delta$ in three-soliton. The detail is as follows:

$$\begin{aligned} \Delta _n=\left| \begin{array}{cccccc} z_{1}^4 \phi _{1,n} &{}z_{1}^2 \phi _{1,n} &{}\phi _{1,n} &{}z_{1}^5 \psi _{1,n} &{}z_{1}^3 \psi _{1,n} &{}z_{1} \psi _{1,n} \\ z_{2}^4 \phi _{2,n} &{}z_{2}^2 \phi _{2,n} &{}\phi _{2,n} &{}z_{2}^5 \psi _{2,n} &{}z_{2}^3 \psi _{2,n} &{}z_{2} \psi _{2,n} \\ z_{3}^4 \phi _{3,n} &{}z_{3}^2 \phi _{3,n} &{}\phi _{3,n} &{}z_{3}^5 \psi _{3,n} &{}z_{3}^3 \psi _{3,n} &{}z_{3} \psi _{3,n} \\ z_{1}^{*2} \psi ^*_{1,n} &{}z_{1}^{*4} \psi ^*_{1,n} &{}z_{1}^{*6} \psi ^*_{1,n} &{}-z^*_{1} \phi ^*_{1,n} &{}-z_{1}^{*3} \phi ^*_{1,n} &{}-z_{1}^{*5} \phi ^*_{1,n} \\ z_{2}^{*2} \psi ^*_{2,n} &{}z_{2}^{*4} \psi ^*_{2,n} &{}z_{2}^{*6} \psi ^*_{2,n} &{}-z^*_{2} \phi ^*_{2,n} &{}-z_{2}^{*3} \phi ^*_{2,n} &{}-z_{2}^{*5} \phi ^*_{2,n} \\ z_{3}^{*2} \psi ^*_{3,n} &{}z_{3}^{*4} \psi ^*_{3,n} &{}z_{3}^{*6} \psi ^*_{3,n} &{}-z^*_{3} \phi ^*_{3,n} &{}-z_{3}^{*3} \phi ^*_{3,n} &{}-z_{3}^{*5} \phi ^*_{3,n} \end{array} \right| ,\nonumber \\ \end{aligned}$$

(31)

where $\Delta a_{n}^{(0)}$,$\Delta b_{n}^{(1)}$ and $\Delta b_{n}^{(5)}$ are given from determinant $\Delta _n$ by replacing its third, sixth and fourth columns with the column vector $(-z^6_1\phi _{1,n}, -z^6_2\phi _{2,n}, -z^6_3\phi _{3,n}, -\psi ^*_{1,n}, -\psi ^*_{2,n}, -\psi ^*_{3,n})^T$.