Skip to main content
SpringerLink
Log in

Employing the dynamics of poles in the complex plane to describe properties of rogue waves: case studies using the Boussinesq and complex modified Korteweg–de Vries equations

  • Original paper
  • Published:
Nonlinear Dynamics Aims and scope Submit manuscript

Abstract

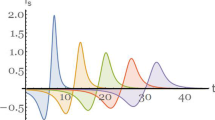
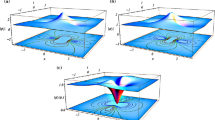
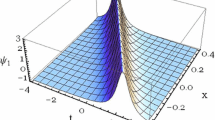
The dynamics and properties of rogue waves of two classical evolution equations are studied in terms of trajectories of the poles of the exact solutions, by analytically continuing the spatial variable to be complex. The Boussinesq equation describes the motion of hydrodynamic waves in two opposite directions in the shallow water regime. The complex modified Korteweg–de Vries equation is relevant for wave packets in nonlinear media governed by a higher-order nonlinear Schrödinger equation, for the special case where second-order dispersion and cubic self-interaction are absent. On examining the movement of poles of the exact solutions for rogue waves, the real parts of the poles correlate well with the locations of maximum displacements in the physical space. This phenomenon holds for high precision numerically for the first-, second- and third-order rogue waves of the Boussinesq equation. A similar principle is also valid for the first- and second-order rogue waves of the complex modified Korteweg–de Vries equation. The imaginary parts of the poles can generate useful information too. For these two evolution models, a smaller imaginary part in the complex plane is associated with a larger amplitude of the rogue wave in physical space. An empirical formula is proposed which works well for the three lowest orders of rogue waves of the Boussinesq equation.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6

Similar content being viewed by others

References

  1. Dysthe, K., Krogstad, H.E., Müller, P.: Oceanic rogue waves. Annu. Rev. Fluid Mech. 40, 287 (2008)

    Article  MathSciNet  Google Scholar 

  2. Onorato, M., Residori, S., Bortolozzo, U., Montina, A., Arecchi, F.T.: Rogue waves and their generating mechanisms in different physical contexts. Phys. Rep. 528, 47 (2013)

    Article  MathSciNet  Google Scholar 

  3. Chen, S., Baronio, F., Soto-Crespo, J.M., Grelu, P., Mihalache, D.: Versatile rogue waves in scalar, vector, and multidimensional nonlinear systems. J. Phys. A Math. Theor. 50, 463001 (2017)

    Article  MathSciNet  Google Scholar 

  4. Chin, S.A., Ashour, O.A., Belić, M.R.: Anatomy of the Akhmediev breather: cascading instability, first formation time, and Fermi–Pasta–Ulam recurrence. Phys. Rev. E 92, 063202 (2015)

    Article  MathSciNet  Google Scholar 

  5. Grinevich, P.G., Santini, P.M.: The exact rogue wave recurrence in the NLS periodic setting via matched asymptotic expansions, for 1 and 2 unstable modes. Phys. Lett. A 382, 973 (2018)

    Article  MathSciNet  Google Scholar 

  6. Kibler, B., Chabchoub, A., Gelash, A., Akhmediev, N., Zakharov, V.E.: Superregular breathers in optics and hydrodynamics: omnipresent modulation instability beyond simple periodicity. Phys. Rev. X 5, 041026 (2015)

    Google Scholar 

  7. Chan, H.N., Chow, K.W.: Rogue waves for an alternative system of coupled Hirota equations: structural robustness and modulation instabilities. Stud. Appl. Math. 139, 78 (2017)

    Article  MathSciNet  Google Scholar 

  8. Whitham, G.B.: Linear and Nonlinear Waves. Wiley, New York (1973)

    MATH  Google Scholar 

  9. Borluk, H., Kalisch, H.: Particle dynamics in the KdV approximation. Wave Motion 49, 691 (2012)

    Article  MathSciNet  Google Scholar 

  10. Hickernell, F.J.: The evolution of large-horizontal-scale disturbances in marginally stable, inviscid, shear flows. II. Solutions of the Boussinesq equation. Stud. Appl. Math. 69, 23 (1983)

    Article  MathSciNet  Google Scholar 

  11. Ablowitz, M.J., Satsuma, J.: Solitons and rational solutions of nonlinear evolution equations. J. Math. Phys. 19, 2180 (1978)

    Article  MathSciNet  Google Scholar 

  12. Ankiewicz, A., Bassom, A.P., Clarkson, P.A., Dowie, E.: Conservation laws and integral relations for the Boussinesq equation. Stud. Appl. Math. 139, 104 (2017)

    Article  MathSciNet  Google Scholar 

  13. Liu, Y., Li, B., An, H.-L.: General high-order breathers, lumps in the (2\(+\)1)-dimensional Boussinesq equation. Nonlinear Dyn. 92, 2061 (2018)

    Article  Google Scholar 

  14. Sun, B., Wazwaz, A.-M.: General high-order breathers and rogue waves in the (3\(+\)1)-dimensional KP–Boussinesq equation. Commun. Nonlinear Sci. Numer. Simul. 64, 1 (2018)

    Article  MathSciNet  Google Scholar 

  15. Zhang, X., Chen, Y.: General high-order rogue waves to nonlinear Schrödinger–Boussinesq equation with the dynamical analysis. Nonlinear Dyn. 93, 2169 (2018)

    Article  Google Scholar 

  16. Li, C., He, J., Porsezian, K.: Rogue waves of the Hirota and the Maxwell–Bloch equations. Phys. Rev. E 87, 012913 (2013)

    Article  Google Scholar 

  17. He, J.S., Wang, L.H., Li, L.J., Porsezian, K., Erdelyi, R.: Few-cycle optical rogue waves: complex modified Korteweg–de Vries equation. Phys. Rev. E 89, 062917 (2013)

    Article  Google Scholar 

  18. Liu, C., Ren, Y., Yang, Z.Y., Yang, W.L.: Superregular breathers in a complex modified Korteweg–de Vries system. Chaos 27, 083120 (2017)

    Article  MathSciNet  Google Scholar 

  19. Zhao, H.Q., Yu, G.F.: Discrete rational and breather solution in the spatial discrete complex modified Korteweg–de Vries equation and continuous counterparts. Chaos 27, 043113 (2017)

    Article  MathSciNet  Google Scholar 

  20. Liu, T., Chiu, T.L., Clarkson, P.A., Chow, K.W.: A connection between the maximum displacements of rogue waves and the dynamics of poles in the complex plane. Chaos 27, 091103 (2017)

    Article  MathSciNet  Google Scholar 

  21. Chiu, T.L., Liu, T.Y., Chan, H.N., Chow, K.W.: The dynamics and evolution of poles and rogue waves for non-linear Schrödinger equations. Commun. Theor. Phys. 68, 290 (2017)

    Article  MathSciNet  Google Scholar 

  22. Konno, K., Ito, H.: Nonlinear interactions between solitons in complex t-plane. I. J. Phys. Soc. Jpn. 56, 897 (1987)

    Article  MathSciNet  Google Scholar 

  23. Konno, K.: Nonlinear interactions between solitons in complex t-plane. II. J. Phys. Soc. Jpn. 56, 1334 (1987)

    Article  MathSciNet  Google Scholar 

  24. Ankiewicz, A., Clarkson, P.A., Akhmediev, N.: Rogue waves, rational solutions, the patterns of their zeros and integral relations. J. Phys. A 43, 122002 (2010)

    Article  MathSciNet  Google Scholar 

  25. Xu, S., He, J.S., Porsezian, K.: Double degeneration on second-order breather solutions of Maxwell–Bloch equation. Wave Motion 80, 82 (2018)

    Article  MathSciNet  Google Scholar 

  26. Chow, K.W.: A class of doubly periodic waves for nonlinear evolution equations. Wave Motion 35, 71 (2002)

    Article  MathSciNet  Google Scholar 

  27. Wen, L.-L., Zhang, H.-Q.: Rogue wave solutions of the (2\(+\)1)-dimensional derivative nonlinear Schrödinger equation. Nonlinear Dyn. 86, 877 (2016)

    Article  Google Scholar 

Download references

Acknowledgements

Partial financial support has been provided by the Research Grants Council through contracts HKU 17200718E, and HKU17200815.

Author information

Authors and Affiliations

  1. Department of Mechanical Engineering, University of Hong Kong, Pokfulam, Hong Kong

    W. C. Chung, T. L. Chiu & K. W. Chow

Authors
  1. W. C. Chung
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. T. L. Chiu
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. K. W. Chow
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to T. L. Chiu.

Ethics declarations

Conflict of interest

The authors declare that there is no conflict of interests regarding the research effort and the publication of this paper.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Chung, W.C., Chiu, T.L. & Chow, K.W. Employing the dynamics of poles in the complex plane to describe properties of rogue waves: case studies using the Boussinesq and complex modified Korteweg–de Vries equations. Nonlinear Dyn 99, 2961–2970 (2020). https://doi.org/10.1007/s11071-020-05475-z

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11071-020-05475-z

Keywords

Search

Navigation