Skip to main content
SpringerLink
Log in

Turing patterns in a predator–prey model on complex networks

  • Original paper
  • Published:
Nonlinear Dynamics Aims and scope Submit manuscript

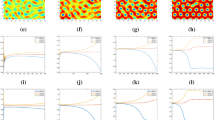
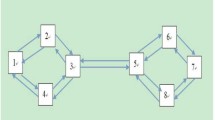
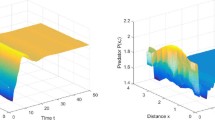
Abstract

Predator–prey model with modified Leslie–Gower and Holling type III schemes governed by reaction–diffusion equations can exhibit diversified pattern formations. Considering that species are usually organized as networks instead of being continuously distributed in space, it is essential to study predator–prey system on complex networks. There are the close relation to discrete predator–prey system and continuous version. Here, we extend predator–prey system from continuous media to random networks via finite volume method. With the help of linear stability analysis, Turing patterns of the Leslie–Gower Holling type III predator–prey model on several different networks are investigated. By contrasting and analyzing numerical simulations, we study the influences of network type, average degree as well as diffusion rate on pattern formations.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6

Similar content being viewed by others

References

  1. Ghosh, P.: Control of the Hopf–Turing transition by time-delayed global feedback in a reaction–diffusion system. Phys. Rev. E 84, 016222 (2011)

    Article  Google Scholar 

  2. Ghorai, S., Poria, S.: Pattern formation in a system involving prey–predation, competition and commensalism. Nonlinear Dyn. 89, 1309–1326 (2017)

    Article  Google Scholar 

  3. Sun, G.Q.: Pattern formation of an epidemic model with diffusion. Nonlinear Dyn. 69, 1097–1104 (2012)

    Article  MathSciNet  Google Scholar 

  4. Rostami, Z., Jafari, S., Perc, M., Slavinec, M.: Elimination of spiral waves in excitable media by magnetic induction. Nonlinear Dyn. 94, 679–692 (2018)

    Article  Google Scholar 

  5. Murray, J.D.: Mathematical Biology II: Spatial Models and Biomedical Applications, 3rd edn. Springer, Berlin (2003)

    Book  Google Scholar 

  6. Brauer, F., Castillo-Chavez, C.: Mathematical Models in Population Biology and Epidemiology, 2nd edn. Springer, Berlin (2012)

    Book  Google Scholar 

  7. Turing, A.M.: The chemical basis of morphogenesis. Philos. Trans. R. Soc. Lond. B Biol. Sci. 237, 37–72 (1952)

    MathSciNet  MATH  Google Scholar 

  8. Kondo, S., Miura, T.: Reaction–diffusion model as a framework for understanding biological pattern formation. Science 329, 1616–1620 (2010)

    Article  MathSciNet  Google Scholar 

  9. Sun, G.Q., Jusup, M., Jin, Z., Wang, Y., Wang, Z.: Pattern transitions in spatial epidemics: mechanisms and emergent properties. Phys. Life Rev. 19, 43–73 (2016)

    Article  Google Scholar 

  10. Malchow, H., Petrovskii, S.V., Venturino, E.: Spatiotemporal Patterns in Ecology and Epidemiology: Theory, Models, and Simulations. Chapman & Hall/CRC Press, London (2008)

    MATH  Google Scholar 

  11. Levin, S., Segel, L.: Hypothesis for origin of planktonic patchiness. Nature 259, 659 (1976)

    Article  Google Scholar 

  12. Sengupta, A., Kruppa, T., Lowen, H.: Chemotactic predator–prey dynamics. Phys. Rev. E 83, 031914 (2011)

    Article  MathSciNet  Google Scholar 

  13. Lai, Y.M., Newby, J., Bressloff, P.C.: Effects of demographic noise on the synchronization of a metapopulation in a fluctuating environment. Phys. Rev. Lett. 107, 118102 (2011)

    Article  Google Scholar 

  14. Zhang, X.C., Sun, G.Q., Jin, Z.: Spatial dynamics in a predator–prey model with Beddington–Deangelis functional response. Phys. Rev. E 85, 021924 (2012)

    Article  Google Scholar 

  15. Choudhury, B.S., Nasipuri, B.: Self-organized spatial patterns due to diffusion in a Holling–Tanner predator–prey model. Comput. Appl. Math. 34, 177–195 (2015)

    Article  MathSciNet  Google Scholar 

  16. Giricheva, E.: Spatiotemporal dynamics of an NPZ model with prey–taxis and intratrophic predation. Nonlinear Dyn. 95, 875–892 (2019)

    Article  Google Scholar 

  17. Jansen, V.A.A., Lloyd, A.L.: Local stability analysis of spatially homogeneous solutions of multi-patch systems. J. Math. Biol. 41, 232–252 (2000)

    Article  MathSciNet  Google Scholar 

  18. Nakao, H., Mikhailov, A.S.: Turing patterns in network-organized activator–inhibitor systems. Nat. Phys. 6, 544–550 (2010)

    Article  Google Scholar 

  19. Fernandes, L.D., de Aguiar, M.A.M.: Turing patterns and apparent competition in predator–prey food webs on networks. Phys. Rev. E 86, 056203 (2012)

    Article  Google Scholar 

  20. Asllani, M., Challenger, J.D., Pavone, F.S., Sacconi, L., Fanelli, D.: The theory of pattern formation on directed networks. Nat. Commun. 5, 4517 (2014)

    Article  Google Scholar 

  21. Asllani, M., Busiello, D.M., Carletti, T., Fanelli, D., Planchon, G.: Turing patterns in multiplex networks. Phys. Rev. E 90, 042814 (2014)

    Article  Google Scholar 

  22. Asllani, M., Carletti, T., Fanelli, D.: Tune the topology to create or destroy patterns. Eur. Phys. J. B 89, 260 (2016)

    Article  MathSciNet  Google Scholar 

  23. Petit, J., Lauwens, B., Fanelli, D., Carletti, T.: Theory of Turing patterns on time varying networks. Phys. Rev. Lett. 119, 148301 (2017)

    Article  Google Scholar 

  24. Mimar, S., Juane, M.M., Park, J., Muñuzuri, A.P., Ghoshal, G.: Turing patterns mediated by network topology in homogeneous active systems. Phys. Rev. E 99, 062303 (2019)

    Article  Google Scholar 

  25. Chang, L.L., Liu, C., Sun, G.Q., Wang, Z., Jin, Z.: Delay-induced patterns in a predator–prey model on complex networks with diffusion. New J. Phys. 21, 073035 (2019)

    Article  MathSciNet  Google Scholar 

  26. Wang, C.X., Chang, L.L., Liu, H.F.: Spatial patterns of a predator–prey system of Leslie type with time delay. PLoS ONE 11, e0150503 (2016)

    Article  Google Scholar 

  27. Nindjina, A.F., Aziz-Alaouib, M.A., Cadivelb, M.: Analysis of a predator–prey model with modified Leslie–Gower and Holling-type II schemes with time delay. Nonlinear Anal. RWA 7, 1104–1118 (2006)

    Article  MathSciNet  Google Scholar 

Download references

Acknowledgements

This study was funded by the National Natural Science Foundation of China (grant numbers 31700393, 11701348), the China Postdoctoral Science Foundation (project 2018T111091) and Key Area R&D Program of Shannxi Province (No. 2019ZDLGY17-07).

Author information

Authors and Affiliations

  1. Center for Ecology and Environmental Sciences, Northwestern Polytechnical University, Xi’an, 710072, Shaanxi, China

    Chen Liu

  2. Complex Systems Research Center, Shanxi University, Taiyuan, 030006, Shanxi, China

    Lili Chang

  3. Institute of Applied Ecology, Chinese Academy of Sciences, Shenyang, 110016, Liaoning, China

    Yue Huang

  4. Center for Optical Imagery Analysis and Learning, Northwestern Polytechnical University, Xi’an, 710072, Shaanxi, China

    Zhen Wang

Authors
  1. Chen Liu
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Lili Chang
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Yue Huang
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Zhen Wang
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Lili Chang.

Ethics declarations

Conflict of interest

The authors declare that they have no conflict of interest.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Liu, C., Chang, L., Huang, Y. et al. Turing patterns in a predator–prey model on complex networks. Nonlinear Dyn 99, 3313–3322 (2020). https://doi.org/10.1007/s11071-019-05460-1

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11071-019-05460-1

Keywords

Search

Navigation