1 Introduction

Discs rotating relative to stationery parts can be found in a wide variety of industrial applications, such as car disc brakes, computer discs, clutches, angular sensors and disc actuators. In the normal operations of these systems, dry friction plays a crucial role. Besides the useful functions they perform, the friction force at the contacting interface may induce unstable vibration of the mechanical components, which greatly influences the performance of these machines or leads to annoying noise. For example, friction-induced noise in cars such as brake squeal is still a major issue in automobile industry today, which may be perceived by customers as quality problems and thereby increase the warrant costs [1].

Dry-friction-induced vibration has been studied extensively, and there are several significant mechanisms proposed to explain the occurrence of friction-induced self-excited vibration: the negative friction slope [2], the stick–slip motion [3], the sprag–slip motion [4] and the mode-coupling instability [5]. The stick–slip motion is characterised by alternating stick and slip regimes. It happens when the static coefficient of friction is greater than the kinetic coefficient of friction or the coefficient of friction decreases with relative velocity [3, 6]. Much of the literature is dedicated to friction-induced stick–slip phenomenon [7,8,9]. Popp and Stelter [3] investigated the discrete and continuous models exhibiting stick–slip motion and rich bifurcation and chaotic behaviours were revealed. Two kinds of friction laws: the Coulomb friction with stiction and the friction model with Stribeck effect, were applied. Kinkaid et al. [10] studied the stick–slip dynamics of a four-DOF (degree-of-freedom) system with friction force in two orthogonal directions on the contact plane and found the change in direction of the friction force can excite unstable vibration even with the Coulomb friction law, thereby introducing a new mechanism for brake squeal. In [11], a systematic procedure to find both stable and unstable periodic stick–slip vibrations of autonomous dynamic systems with dry friction was derived, in which the discontinuous friction forces were approximated by a smooth function. Hetzler [12] studied the effect of damping due to Coulomb friction on a simple oscillator exhibiting self-excitation due to negative damping. Tonazzi et al. [13] performed an experimental and numerical analysis of frictional contact scenarios from macro stick–slip to continuous sliding. Feeny et al. [14] presented a historical review of dry friction and stick–slip phenomena in structural and mechanical systems. The sprag–slip concept was firstly proposed by Spurr [4], in which the variations of normal and tangential forces due to the deformations of contacting structures were considered to cause the vibration instability. Hoffmann and Gaul [15] examined the dynamics of sprag–slip instability and found that there were parameter combinations for which the system did not possess a static solution corresponding to a steady sliding state, which could be a sufficient condition for occurrence of sprag–slip oscillation. Sinou et al. [16] studied the instability in a nonlinear sprag–slip model with constant coefficient of friction by a central manifold theory. The mode-coupling instability occurred as some modes of the system became unstable when coupling with other modes as a result of friction-induced cross-coupling force. Hoffmann et al. [17] used a two-DOF model to clarify the physical mechanisms underlying the mode-coupling instability of self-excited friction-induced vibration. The effect of viscous damping on the mode-coupling instability in friction-induced vibration was investigated in [18]. Kang et al. [19] studied the dynamic instability of a thin circular plate with friction interface and established the formulation of modal instability due to the mode coupling of the transverse doublet modes. In the case of high-frequency excitation, some non-trivial effects such as shifting of the equilibrium point and dry friction behaving as linear viscous damping can occur to the system dynamics [20, 21].

There were also other friction-related factors responsible for exciting unstable vibration and noise. Chan et al. [22] revealed the destabilising effect of the friction force as a follower force. By using the LuGre friction model, Feng et al. [23] studied the chaotic motions on an autonomous single-degree-of-freedom oscillator because the friction model contains one internal variable. Besides, Butlin and Woodhouse [24] analysed the sensitivity of friction-induced vibration to parameter changes in idealised systems. Wang and Woodhouse [25] developed a novel tribometer to measure the linearised frequency response function for sliding friction, which could provide the input data needed for squeal prediction. Nordmark et al. [26] explored the possibility to formulate a consistent and unambiguous forward simulation model of planar rigid-body mechanical systems with isolated points of intermittent or sustained contact with rigid constraining surfaces in the presence of dry friction. Saha et al. [27] investigated two different friction models by examining the dynamic responses of a single-degree-of-freedom system exhibiting friction-induced vibration. Marques et al. [28] presented a comprehensive review of literature on friction force models and demonstrated the influence of the various friction models on the dynamic response of the multibody mechanical systems with friction.

The dynamic instabilities of an elastic disc under a mass–spring–damper loading system rotating relative to the disc were studied in [29, 30]. In [22], the parametric resonances of an annular plate excited by a rotating transverse load system with frictional follower force were examined and the results showed the friction force could be a destabilising factor. Ouyang and Mottershead [31] investigated the vibration of a disc excited by two co-rotating sliders on either side of a disc and the moving normal forces and friction couple produced by the sliders were seen to bring about dynamic instability. A slider–mass system driven around the surface of a flexible disc was studied in [32], where the in-plane vibration of the slider was considered and coupled with the transverse vibration of the disc through the normal contact force. Subsequently, Li et al. [33] used a similar model but incorporated the separation and reattachment phenomena considering the possibility of loss of contact due to growing transverse disc vibration and the results highlighted the important role of separation on friction-induced vibration. Hochlenert et al. [34] studied the self-excited vibrations in a moving beam and plate generated by frictional forces and an accurate formulation of the kinematics of the frictional contact in two or three dimensions was established. Kang et al. [35] conducted a comprehensive stability analysis of disc brake vibration with gyroscopic, negative friction slope and mode-coupling mechanisms included by modelling the disc and pads as rotating annular and stationary annular sector plates, respectively. Sui and Ding [36] investigated the instability of a pad-on-disc in moving interactions and a stochastic analysis was carried out. The dynamics of an asymmetric spinning disc under stationary friction loads was investigated in [37], and the analysis showed that the stability boundaries of the system were altered by the loss of axisymmetry of the disc.

The models used to study the friction-induced vibration (FIV) problems in the existing literature usually employ a constant sliding velocity, e.g. constant belt velocity in the slider-on-belt model or constant spinning speed of the disc. There has been little research that has considered the decelerating or accelerating sliding, which should not be neglected as an important influential factor in friction-induced-vibration. In [38], a mathematical model was presented to prove that stick–slip oscillation could be induced by deceleration. Pilipchuk et al. [39] examined the friction-induced dynamics of a two-DOF (degree-of-freedom) ‘belt–spring–block’ model and showed that due to the decelerating belt, the system response experiences transitions which could be regarded as simple indicators of onset of squeal. Recently, Dombovari et al. put forward a method to investigate the stability property of the quasi-stationary solution for a smooth dynamic system with slowly time-varying parameters [40]. However, the work on the friction-induced dynamics under decelerating/accelerating sliding motion is still quite limited. To investigate the influences of decelerating/accelerating sliding on the dynamic behaviour of frictional systems and study the problems such as brake noise in a more realistic model because the braking process is practically a decelerating process for the brake disc, the friction-induced vibration of a mass–slider on a spinning elastic disc at variable speeds is examined in this paper.

The rest of the paper is arranged as follows. In Sect. 2, the system configuration of the slider-on-disc model is introduced and the equations of motion for the system in three different states: stick, slip and separation, are derived. The conditions for the transitions among these states are determined. Subsequently, the numerical simulation and analysis are conducted to investigate the distinct dynamic behaviours of the system in the three different situations of spinning speed of disc in Sect. 3 and to help reveal the effects of deceleration and acceleration on the friction-induced dynamics of the system, the system responses under the decelerating and accelerating sliding motion are compared with the results under constant sliding speed. The significant differences that the deceleration and acceleration make to the vibration behaviour of the frictional system from that in the constant disc speed underlie the necessity to consider the time-variant spinning speed in the research of friction-induced vibration and noise. Finally, in Sect. 4 the conclusions on the effects of the decelerating and accelerating sliding motion on the dynamics of the frictional system are drawn.

2 Model description and theoretical analysis

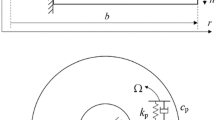
The dynamics of a slider-on-disc system subject to friction force is studied in this paper. The disc is modelled as a Kirchhoff plate clamped at inner boundary and free at outer boundary. A slider, which is assumed to be a point mass, is connected to the rigid base with transverse and in-plane (circumferential) springs and dashpots and in point contact with the spinning disc. Without loss of generality, the circumferential coordinate of the fixed base is set as \(\theta =0\). The slider is assumed to be fixed radially at \(r_0\) from the disc centre and pre-compressed on the disc by \(N_0\) in the normal direction. The system configuration is illustrated in Fig. 1. Three different situations of spinning speed of disc, i.e. constant deceleration, constant acceleration and constant speed, are considered, which can be expressed as,

$$\begin{aligned} {\varOmega }(t)= & {} {\varOmega }_0 \left( {1-\frac{t}{t_{\mathrm{max}}}}\right) , \quad \hbox {decelerating} \end{aligned}$$
(1)
$$\begin{aligned} {\varOmega }(t)= & {} {\varOmega }_1 +ct, \quad \hbox {accelerating} \end{aligned}$$
(2)
$$\begin{aligned} {\varOmega }(t)= & {} {\varOmega }_{\mathrm{c}}, \quad \hbox {constant speed} \end{aligned}$$
(3)
Fig. 1
figure 1

The system configuration

Full size image

for the three situations, respectively, as shown in Fig. 2. In Eq. (1), \({\varOmega }_0\) is the initial spinning speed of the disc and \(t_{\mathrm{max}}\) is the time duration of the deceleration process. In Eq. (2), \({\varOmega }_1\) is the initial spinning speed of the disc and c is the acceleration of the disc speed and always positive. In Eq. (3), \({\varOmega }_{\mathrm{c}}\) is a constant value which is independent of time.

Fig. 2
figure 2

The three situations of spinning speed of the disc

Full size image

2.1 Circumferential stick–slip vibration of the slider

When the circumferential relative velocity between the slider and the disc is not equal to zero, the slider slips on the disc. In the slip phase, the slider is subject to the kinetic friction force; thus, the equation of circumferential motion of the slider can be written as,

$$\begin{aligned} I \ddot{{\varphi }} + r_{0}^{2} c_{{\varphi }} {\dot{{\varphi }}} + r_{0}^{2} k_{{\varphi }} {\varphi }= r_{0} \hbox {sgn} ({\varOmega }- {\dot{{\varphi }}}) \mu N \end{aligned}$$
(4)

where \({\varphi }\) is the circumferential angular displacement of the slider, \(I=mr_0^2\) and \(c_{\varphi }\) and \(k_{\varphi }\) are its moment of inertia, in-plane damping coefficient and in-plane spring stiffness, respectively. m is the slider’s mass, and N represents the normal force between the disc and the slider. \(\mu \) is the kinetic friction coefficient, and here, it is taken as a function of the relative velocity [41] as follows,

$$\begin{aligned} \mu =\mu _1 + ({\mu _0 -\mu _1}) \hbox {e}^{-\alpha |{r_0 ({{\varOmega }- {\dot{{\varphi }}}})}|} \end{aligned}$$
(5)

where \(\mu _0, \mu _1, \alpha \) are the parameters determining the maximum value, the asymptotic value and the initial slope of the friction coefficient with respect to the relative velocity.

When the circumferential velocity of slider reaches the instantaneous disc speed and the magnitude of the friction force acting on the slider does not exceed the static friction force, the slider sticks to the disc. In the sticking phase, the circumferential angular velocity and acceleration of the slider remain identical to the disc’s rotary speed and acceleration, i.e.

$$\begin{aligned} {\dot{{\varphi }}} = {\varOmega }, \ddot{{\varphi }} = {\dot{{\varOmega }}} \end{aligned}$$
(6)

Substituting Eqs. (1)–(3) into Eq. (6), it is easy to derive that,

$$\begin{aligned} {\dot{{\varphi }}}= & {} {\varOmega }_{0} \left( 1- {\frac{t}{t_{\mathrm{max}}}}\right) , \ddot{{\varphi }} = - {\frac{{\varOmega }_{0}}{t_{\mathrm{max}}}} \end{aligned}$$
(7)
$$\begin{aligned} {\dot{{\varphi }}}= & {} {\varOmega }_{1} + {ct}, \ddot{{\varphi }} = c \end{aligned}$$
(8)
$$\begin{aligned} {\dot{{\varphi }}}= & {} {\varOmega }_{\mathrm{c}}, \ddot{{\varphi }} = 0 \end{aligned}$$
(9)

in the sticking phase for the situations of decelerating disc, accelerating disc and constant disc speed, respectively. The instantaneous circumferential position of the slider in the sticking phase is thus given by,

$$\begin{aligned} {\varphi }(t)= & {} {\varphi }({t_q}) + \int _{t_q}^t {\varOmega }_0 \left( {1-\frac{t}{t_{\mathrm{max}}}} \right) \, \hbox {d}t \nonumber \\= & {} {\varphi }({t_q}) + {\varOmega }_0 ({t-t_q}) - \frac{{\varOmega }_0}{2t_{\mathrm{max}}} \left( {t^{2}-t_q^2}\right) \end{aligned}$$
(10)
$$\begin{aligned} {\varphi }(t)= & {} {\varphi }({t_q}) + \int _{t_q}^t ({{\varOmega }_1 +ct}) \, \hbox {d}t \nonumber \\= & {} {\varphi }({t_q}) + {\varOmega }_1 ({t-t_q}) + \frac{1}{2}c \left( {t^{2}-t_q^2}\right) \end{aligned}$$
(11)
$$\begin{aligned} {\varphi }(t)= & {} {\varphi }({t_q}) + \int _{t_q}^t {\varOmega }_{\mathrm{c}} \, \hbox {d}t = {\varphi }({t_q}) + {\varOmega }_{\mathrm{c}} ({t-t_q}) \end{aligned}$$
(12)

for the situations of decelerating disc, accelerating disc and constant disc speed, respectively, where \(t_q\) is the time instant when a sticking phase starts. And the friction force in the sticking phase is a reaction force, which can be obtained as,

$$\begin{aligned} f_{\mathrm{stick}} =\frac{1}{r_0} \left( I \ddot{{\varphi }} + r_{0}^{2} c_{{\varphi }} {\dot{{\varphi }}} + r_{0}^{2} k_{{\varphi }} {{\varphi }}\right) \end{aligned}$$
(13)

Thus, the condition for the slider to remain sticking to the disc is,

$$\begin{aligned} \left| \frac{1}{r_0} \left( I \ddot{{\varphi }} + r_{0}^{2} c_{{\varphi }} {\dot{{\varphi }}} + r_{0}^{2} k_{{\varphi }} {{\varphi }}\right) \right| \le \mu _{\mathrm{s}} N \end{aligned}$$
(14)

where \(\mu _{\mathrm{s}}\) is the static friction coefficient between the slider and the disc. When the magnitude of the friction force reaches the maximum static friction capacity, the slider starts to slip on the disc again.

2.2 Transverse vibration of the disc

The slider is located at the polar coordinate \(({r_0, {\varphi }(t)})\) at an arbitrary time t. When the slider is in contact with the disc, the normal displacement z(t) of the slider equals to the local transverse displacement of the disc at \(({r_0, {\varphi }(t)})\) in the space-fixed coordinate system [42], i.e.

$$\begin{aligned} z(t) = w ({r_0, {\varphi }(t), t}) \end{aligned}$$
(15)

and thus,

$$\begin{aligned} {\dot{z}}= & {} \frac{\partial w}{\partial t} + {\dot{{\varphi }}} \frac{\partial w}{\partial {\varphi }} \end{aligned}$$
(16)
$$\begin{aligned} \ddot{z}= & {} \frac{{\partial }^{2} w}{\partial {t}^{2}} + 2 {\dot{{\varphi }}} \frac{{\partial }^{2} w}{\partial {\varphi }\partial t} + {{\dot{{\varphi }}}}^{2} \frac{{\partial }^{2} w}{\partial {{\varphi }}^{2}} + \ddot{{\varphi }} \frac{\partial w}{\partial t} \end{aligned}$$
(17)

By the force balance in the normal direction of the slider, the normal force between the slider and the disc is obtained as,

$$\begin{aligned} N = N_0 +m \ddot{z} + c_{z} {\dot{z}} + k_{z} z \end{aligned}$$
(18)

Meanwhile, the friction force between the slider and disc presents a bending moment in the circumferential direction of the disc [19, 29], which is,

$$\begin{aligned} M_\theta =hf/2 \end{aligned}$$
(19)

where h is the thickness of the disc. During the slip phase, the friction force reads,

$$\begin{aligned} f= & {} \hbox {sgn} ({{\varOmega }- {\dot{{\varphi }}}}) \mu N \nonumber \\= & {} \hbox {sgn} ({{\varOmega }- {\dot{{\varphi }}}}) \mu ({N_0 + m {\ddot{z}} + c_{z} {\dot{z}} + k_{z} z}) \end{aligned}$$
(20)

While in the stick phase, the friction force, given in Eq. (13), can be written as,

$$\begin{aligned} f= & {} \frac{1}{r_0}\left[ -I\frac{{\varOmega }_0}{t_{\mathrm{max}}} +r_0^2 c_{\varphi }{\varOmega }_0 \left( {1-\frac{t}{t_{\mathrm{max}}}} \right) + r_0^2 k_{\varphi }{\varphi }\right] \nonumber \\ \end{aligned}$$
(21)
$$\begin{aligned} f= & {} \frac{1}{r_0}\left[ {Ic+r_0^2 c_{\varphi }({{\varOmega }_1 +ct}) + r_0^2 k_{\varphi }{\varphi }}\right] \end{aligned}$$
(22)
$$\begin{aligned} f= & {} \frac{1}{r_0} \left( {r_0^2 c_{\varphi }{\varOmega }_{\mathrm{c}} +r_0^2 k_{\varphi }{\varphi }}\right) \end{aligned}$$
(23)

for the situations of decelerating, accelerating and constant speed, respectively, where \({\varphi }\) can be obtained from Eqs. (10)–(12), respectively. The transverse displacement of the disc in the space-fixed coordinate system can be approximated by a linear superposition of a set of orthogonal basis functions as [43],

$$\begin{aligned} w ({r,\theta , t})= & {} \sum \limits _{k=0}^\infty \sum \limits _{l=0}^\infty R_{kl} (r) \nonumber \\&[\hbox {cos} ({l\theta }) \cdot C_{kl} (t) + \hbox {sin} ({l\theta }) \cdot D_{kl} (t)] \end{aligned}$$
(24)

where k and l denote the number of nodal circles and nodal diameters, respectively, \(C_{kl} (t)\), \(D_{kl} (t)\) are modal coordinates and \(R_{kl} (r)\) is a combination of Bessel functions satisfying the inner and outer boundary conditions of the nonrotating disc and orthogonality conditions. And the equations of motion with respect to the modal coordinates can be obtained from Lagrange’s equations,

$$\begin{aligned}&\frac{\hbox {d}}{\hbox {d}t} \left[ {\frac{\partial L}{\partial {\dot{C}}_{kl}}}\right] - {\frac{\partial L}{\partial {C}_{kl}}} = P_{kl}, \nonumber \\&\quad k = 0,1,2,\dots , \infty , l = 0,1,2,\dots , \infty \end{aligned}$$
(25)
$$\begin{aligned}&\frac{\hbox {d}}{\hbox {d}t} \left[ {\frac{\partial L}{\partial {\dot{D}}_{kl}}}\right] - {\frac{\partial L}{\partial {D}_{kl}}} = Q_{kl}, \nonumber \\&\quad k = 0,1,2,\dots , \infty , l = 1,2,\dots , \infty \end{aligned}$$
(26)

in which

$$\begin{aligned}&L=T-U \end{aligned}$$
(27)
$$\begin{aligned}&T=\frac{1}{2}\rho h {\iint }_A \left( {\frac{\partial w ({r,\theta , t})}{\partial t}+{\varOmega }\frac{\partial w ({r,\theta ,t})}{\partial \theta }}\right) ^{2}\nonumber \\&\qquad r\hbox {d}r\hbox {d}\theta \end{aligned}$$
(28)
$$\begin{aligned}&U=\frac{1}{2}D \iint _A ({\nabla ^{2}w})^{2}-2 ({1-\nu }) \nonumber \\&\qquad \times \left[ \frac{\partial ^{2}w}{\partial r^{2}} \left( {\frac{1}{r}\frac{\partial w}{\partial r}+\frac{1}{r^{2}}\frac{\partial ^{2}w}{\partial \theta ^{2}}} \right) \right. \nonumber \\&\qquad \left. - \left( {\frac{1}{r}\frac{\partial ^{2}w}{\partial r\partial \theta }-\frac{1}{r^{2}}\frac{\partial w}{\partial \theta }} \right) ^{2} \right] \, r\hbox {d}r\hbox {d}\theta \end{aligned}$$
(29)
$$\begin{aligned}&P_{kl} =-N\cdot \frac{\partial w ({r_0, {\varphi }, t})}{\partial C_{kl}} +M_\theta \frac{\partial \gamma }{\partial C_{kl}} \end{aligned}$$
(30)
$$\begin{aligned}&Q_{kl} =-N\cdot \frac{\partial w ({r_0 ,{\varphi },t})}{\partial D_{kl}}+M_\theta \frac{\partial \gamma }{\partial D_{kl}} \end{aligned}$$
(31)
$$\begin{aligned}&\gamma =\frac{\partial w ({r_0 ,{\varphi },t})}{r_0 \partial \theta } \end{aligned}$$
(32)

In the above equations, T and U represent the kinetic energy and strain energy of the disc, respectively, and \(P_{kl}\) and \(Q_{kl}\) represent the generalised forces obtained from the virtual work of the normal force and bending moment acting on the disc. A is the area of the disc surface, \(\rho \) is the density of material, \(D = \frac{Eh^{3}}{12 ({1-\nu ^{2}})}\) is the bending rigidity, and E and \(\nu \) are the Young’s modulus and the Poisson’s ratio of the disc material, respectively.

2.3 Coupled in-plane and out-of-plane vibration

Substituting Eqs. (15)–(20) and (24) into Eqs. (25)–(32), the equations of the transverse motion of the disc with respect to the modal coordinates during the slip phase are given,

$$\begin{aligned}&M_{kl} {\ddot{C}}_{kl} + 2lM_{kl} {\varOmega }{\dot{D}}_{kl} + \left( \omega _{kl}^2 M_{kl}- l^{2} M_{kl} {\varOmega }^{2}\right) C_{kl} \nonumber \\&\quad = \left[ - R_{kl} (r_{0}) \hbox {cos} (l {\varphi }) \right. \nonumber \\&\qquad \left. -\, \frac{h}{2r_{0}} {\textit{sgn}} ({\varOmega }- {\dot{{\varphi }}}) \mu l R_{kl} (r_{0}) \hbox {sin} (l {\varphi })\right] \nonumber \\&\qquad \cdot \left( N_{0} +{\sum }_{r= 0}^{\infty } {\sum }_{s= 0}^{\infty } R_{rs} (r_{0}) \right. \nonumber \\&\qquad \quad \Bigg \{m\hbox {cos} (s{\varphi }) {\ddot{C}}_{rs} + m\hbox {sin} (s{\varphi }) {\ddot{D}}_{rs} \nonumber \\&\qquad +\, [-2 m {\dot{{\varphi }}} s\hbox {sin} (s{\varphi }) + c_{z} \hbox {cos} (s{\varphi })] {\dot{C}}_{rs} \nonumber \\&\qquad +\, [2 m {\dot{{\varphi }}} s\hbox {cos} (s{\varphi }) + c_{z} \hbox {sin} (s{\varphi })] {\dot{D}}_{rs} \nonumber \\&\qquad +\, [- m{\ddot{{\varphi }}} s\hbox {sin} (s{\varphi }) - m {\dot{{\varphi }}}^{2} s^{2} \hbox {cos} (s{\varphi }) \nonumber \\&\qquad -\, c_{z} {\dot{{\varphi }}} s\hbox {sin} (s{\varphi }) + k_{z} \hbox {cos} (s{\varphi })] C_{rs} \nonumber \\&\qquad +\, [m{\ddot{{\varphi }}} s\hbox {cos} (s{\varphi }) - m {\dot{{\varphi }}}^{2} s^{2} \hbox {sin} (s{\varphi }) \nonumber \\&\qquad \left. +\, c_{z} {\dot{{\varphi }}} s\hbox {cos} (s{\varphi }) + k_{z} \hbox {sin} (s{\varphi })] D_{rs} \Big \}\right) \end{aligned}$$
(33)
$$\begin{aligned}&M_{kl} {\ddot{D}}_{kl} + 2lM_{kl} {\varOmega }{\dot{C}}_{kl} + \left( \omega _{kl}^2 M_{kl} - l^{2} M_{kl} {\varOmega }^{2}\right) D_{kl} \nonumber \\&\quad = \left[ - R_{kl} (r_{0}) \hbox {sin} (l {\varphi }) \right. \nonumber \\&\qquad \left. +\, \frac{h}{2r_{0}} {\textit{sgn}} ({\varOmega }- {\dot{{\varphi }}}) \mu l R_{kl} (r_{0}) \hbox {cos} (l {\varphi })\right] \nonumber \\&\qquad \cdot \left( N_{0}+ \sum \limits _{r= 0}^{\infty } \sum \limits _{s= 0}^{\infty } R_{rs} (r_{0}) \right. \nonumber \\&\qquad \Big \{m\hbox {cos} (s{\varphi }) {\ddot{C}}_{rs} + m\hbox {sin} (s{\varphi }) {\ddot{D}}_{rs} \nonumber \\&\qquad +\, [-2 m {\dot{{\varphi }}} s\hbox {sin} (s{\varphi }) + c_{z} \hbox {cos} (s{\varphi })] {\dot{C}}_{rs} \nonumber \\&\qquad +\, [2 m {\dot{{\varphi }}} s\hbox {cos} (s{\varphi }) + c_{z} \hbox {sin} (s{\varphi })] {\dot{D}}_{rs} \nonumber \\&\qquad +\, [- m{\ddot{{\varphi }}} s\hbox {sin} (s{\varphi }) - m {\dot{{\varphi }}}^{2} s^{2} \hbox {cos} (s{\varphi }) \nonumber \\&\qquad -\, \, c_{z} {\dot{{\varphi }}} s\hbox {sin} (s{\varphi }) + k_{z} \hbox {cos} (s{\varphi })] C_{rs} \nonumber \\&\qquad +\, [m{\ddot{{\varphi }}} s\hbox {cos} (s{\varphi }) - m {\dot{{\varphi }}}^{2} s^{2} \hbox {sin} (s{\varphi }) \nonumber \\&\qquad \left. +\, c_{z} {\dot{{\varphi }}} s\hbox {cos} (s{\varphi }) + k_{z} \hbox {sin} (s{\varphi })] D_{rs} \Big \}\right) \end{aligned}$$
(34)

where \({\varOmega }\) is given by Eqs. (1)–(3) for the situations of decelerating disc, accelerating disc and constant disc speed, respectively, \(\omega _{kl}\) is the natural frequency of the mode with k nodal circles and l nodal diameters of the corresponding nonrotating plate, and

$$\begin{aligned} M_{kl} = \left\{ \begin{array}{ll} \rho h {\pi } {\int }_a^b R_{kl}^2 (r)r\hbox {d}r, &{}\quad l=1,2,\dots \\ 2\rho h {\pi } {\int }_a^b R_{kl}^2 (r)r\hbox {d}r, &{} \quad l=0 \\ \end{array} \right. \end{aligned}$$
(35)

During the slip phase, the equation of motion of \({\varphi }\) reads,

$$\begin{aligned} \begin{aligned}&I \ddot{{\varphi }} + r_{0}^{2} c_{{\varphi }} {\dot{{\varphi }}} + r_{0}^{2} k_{{\varphi }} {{\varphi }} \\&\quad = r_{0} {\text {sgn}} ({\varOmega }- {\dot{{\varphi }}}) \mu \\&\qquad \left( N_{0}+ \sum _{r= 0}^{\infty } \sum _{s= 0}^{\infty } R_{rs} (r_{0}) \right. \\&\qquad \{m\hbox {cos} (s{\varphi }) {\ddot{C}}_{rs} + m\hbox {sin} (s{\varphi }) {\ddot{D}}_{rs} \\&\qquad +\, [-2 m {\dot{{\varphi }}} s\hbox {sin} (s{\varphi }) + c_{z} \hbox {cos} (s{\varphi })] {\dot{C}}_{rs} \\&\qquad + \,[2 m {\dot{{\varphi }}} s\hbox {cos} (s{\varphi }) + c_{z} \hbox {sin} (s{\varphi })] {\dot{D}}_{rs} \\&\qquad +\, [- m{\ddot{{\varphi }}} s\hbox {sin} (s{\varphi }) - m {\dot{{\varphi }}}^{2} s^{2} \hbox {cos} (s{\varphi }) \\&\qquad -\, c_{z} {\dot{{\varphi }}} s\hbox {sin} (s{\varphi }) + k_{z} \hbox {cos} (s{\varphi })] C_{rs} \\&\qquad +\, [m{\ddot{{\varphi }}} s\hbox {cos} (s{\varphi }) - m {\dot{{\varphi }}}^{2} s^{2} \hbox {sin} (s{\varphi }) \\&\qquad \left. +\, c_{z} {\dot{{\varphi }}} s\hbox {cos} (s{\varphi }) + k_{z} \hbox {sin} (s{\varphi })] D_{rs} \}\right) \end{aligned} \end{aligned}$$
(36)

In the stick phase, the equations of the transverse motion of the disc can be derived by substituting Eqs. (15)–(19) and (24) into Eqs. (25)–(32) as,

$$\begin{aligned}&M_{kl} {\ddot{C}}_{kl} + 2lM_{kl} {\varOmega }{\dot{D}}_{kl} + \left( \omega _{kl}^2 M_{kl}- l^{2} M_{kl} {\varOmega }^{2}\right) C_{kl} \nonumber \\&\quad = - \frac{h}{2r_{0}} l R_{kl} (r_{0}) \hbox {sin} (l {\varphi })f - R_{kl} (r_{0}) \hbox {cos} (l {\varphi })\nonumber \\&\qquad \cdot \left( N_{0}+ \sum \limits _{r= 0}^{\infty } \sum \limits _{s= 0}^{\infty } R_{rs} (r_{0}) \right. \nonumber \\&\qquad \Big \{m\hbox {cos} (s{\varphi }) {\ddot{C}}_{rs} + m\hbox {sin} (s{\varphi }) {\ddot{D}}_{rs} \nonumber \\&\qquad +\, [-2 m {\dot{{\varphi }}} s\hbox {sin} (s{\varphi }) + c_{z} \hbox {cos} (s{\varphi })] {\dot{C}}_{rs} \nonumber \\&\qquad +\, [2 m {\dot{{\varphi }}} s\hbox {cos} (s{\varphi }) + c_{z} \hbox {sin} (s{\varphi })] {\dot{D}}_{rs} \nonumber \\&\qquad +\, [- m{\ddot{{\varphi }}} s\hbox {sin} (s{\varphi }) - m {\dot{{\varphi }}}^{2} s^{2} \hbox {cos} (s{\varphi }) \nonumber \\&\qquad -\, c_{z} {\dot{{\varphi }}} s\hbox {sin} (s{\varphi }) + k_{z} \hbox {cos} (s{\varphi })] C_{rs} \nonumber \\&\qquad +\, [m{\ddot{{\varphi }}} s\hbox {cos} (s{\varphi }) - m {\dot{{\varphi }}}^{2} s^{2} \hbox {sin} (s{\varphi }) \nonumber \\&\qquad \left. +\, c_{z} {\dot{{\varphi }}} s\hbox {cos} (s{\varphi }) + k_{z} \hbox {sin} (s{\varphi })] D_{rs} \}\right) \end{aligned}$$
(37)
$$\begin{aligned}&M_{kl} {\ddot{D}}_{kl} + 2lM_{kl} {\varOmega }{\dot{C}}_{kl} + \left( \omega _{kl}^2 M_{kl}- l^{2} M_{kl} {\varOmega }^{2}\right) D_{kl} \nonumber \\&\quad = - \frac{h}{2r_{0}} l R_{kl} (r_{0}) \hbox {cos} (l {\varphi })f - R_{kl} (r_{0}) \hbox {sin} (l {\varphi })\nonumber \\&\qquad \cdot \left( N_{0}+ \sum \limits _{r= 0}^{\infty } \sum \limits _{s= 0}^{\infty } R_{rs} (r_{0}) \right. \nonumber \\&\qquad \Big \{m\hbox {cos} (s{\varphi }) {\ddot{C}}_{rs} + m\hbox {sin} (s{\varphi }) {\ddot{D}}_{rs} \nonumber \\&\qquad +\, [-2 m {\dot{{\varphi }}} s\hbox {sin} (s{\varphi }) + c_{z} \hbox {cos} (s{\varphi })] {\dot{C}}_{rs} \nonumber \\&\qquad +\, [2 m {\dot{{\varphi }}} s\hbox {cos} (s{\varphi }) + c_{z} \hbox {sin} (s{\varphi })] {\dot{D}}_{rs} \nonumber \\&\qquad + \,[- m{\ddot{{\varphi }}} s\hbox {sin} (s{\varphi }) - m {\dot{{\varphi }}}^{2} s^{2} \hbox {cos} (s{\varphi }) \nonumber \\&\qquad - c_{z} {\dot{{\varphi }}} s\hbox {sin} (s{\varphi }) + k_{z} \hbox {cos} (s{\varphi })] C_{rs} \nonumber \\&\qquad + \,[m{\ddot{{\varphi }}} s\hbox {cos} (s{\varphi }) - m {\dot{{\varphi }}}^{2} s^{2} \hbox {sin} (s{\varphi }) \nonumber \\&\qquad \left. +\, c_{z} {\dot{{\varphi }}} s\hbox {cos} (s{\varphi }) + k_{z} \hbox {sin} (s{\varphi })] D_{rs} \Big \}\right) \end{aligned}$$
(38)

where f is given by Eqs (21)–(23) for the situations of decelerating disc, accelerating disc and constant disc speed, respectively, and \({\varphi }, {\dot{{\varphi }}}, \ddot{{\varphi }}\) during the stick phase for the three different situations are given in Eqs. (7)–(12). The condition for remaining in the stick state, which is given in Eq. (14), is thus obtained as

$$\begin{aligned} \begin{aligned}&\left| \frac{1}{r_{0}} \left( I \ddot{{\varphi }} + r_{0}^{2} c_{{\varphi }} {\dot{{\varphi }}} + r_{0}^{2} k_{{\varphi }} {{\varphi }}\right) \right| \\&\quad \le \mu _{s} \left( N_{0}+ \sum \limits _{r= 0}^{\infty } \sum \limits _{s= 0}^{\infty } R_{rs} (r_{0}) \right. \\&\qquad \Big \{m\hbox {cos} (s{\varphi }) {\ddot{C}}_{rs} + m\hbox {sin} (s{\varphi }) {\ddot{D}}_{rs} \\&\qquad + [-2 m {\dot{{\varphi }}} s\hbox {sin} (s{\varphi }) + c_{z} \hbox {cos} (s{\varphi })] {\dot{C}}_{rs} \\&\qquad + [2 m {\dot{{\varphi }}} s\hbox {cos} (s{\varphi }) + c_{z} \hbox {sin} (s{\varphi })] {\dot{D}}_{rs} \\&\qquad + [- m{\ddot{{\varphi }}} s\hbox {sin} (s{\varphi }) - m {\dot{{\varphi }}}^{2} s^{2} \hbox {cos} (s{\varphi }) \\&\qquad - c_{z} {\dot{{\varphi }}} s\hbox {sin} (s{\varphi }) + k_{z} \hbox {cos} (s{\varphi })] C_{rs} \\&\qquad + [m{\ddot{{\varphi }}} s\hbox {cos} (s{\varphi }) - m {\dot{{\varphi }}}^{2} s^{2} \hbox {sin} (s{\varphi }) \\&\qquad \left. + c_{z} {\dot{{\varphi }}} s\hbox {cos} (s{\varphi }) + k_{z} \hbox {sin} (s{\varphi })] D_{rs} \Big \}\right) \end{aligned} \end{aligned}$$
(39)

2.4 Separation and re-contact

With the increase in the amplitude of the transverse motion, the slider may separate from the disc. Separation happens when the normal force between the disc and the slider drops to \(N=0\). And in the separation phase, both the slider and the disc experience free vibration; therefore, the equations of motion of the disc and the slider read,

$$\begin{aligned}&M_{kl} {\ddot{C}}_{kl} + 2lM_{kl} {\varOmega }{\dot{D}}_{kl} \nonumber \\&\quad + \left( \omega _{kl}^2 M_{kl}- l^{2} M_{kl} {\varOmega }^{2}\right) C_{kl} = 0 \end{aligned}$$
(40)
$$\begin{aligned}&M_{kl} {\ddot{D}}_{kl} + 2lM_{kl} {\varOmega }{\dot{C}}_{kl} \nonumber \\&\quad + \left( \omega _{kl}^2 M_{kl}- l^{2} M_{kl} {\varOmega }^{2}\right) D_{kl} = 0 \end{aligned}$$
(41)

for the transverse displacement of the disc, and

$$\begin{aligned}&I \ddot{{\varphi }} + r_{0}^{2} c_{{\varphi }} {\dot{{\varphi }}} + r_{0}^{2} k_{{\varphi }} {{\varphi }} = 0 \end{aligned}$$
(42)
$$\begin{aligned}&m\ddot{z} + c{\dot{z}} + kz + N_{0} = 0 \end{aligned}$$
(43)

for the circumferential and normal motions of the slider. The state of separation is maintained when the following condition is satisfied,

$$\begin{aligned} z(t) > w ({r_0, {\varphi }(t), t}) \end{aligned}$$
(44)

After separation, the above condition is monitored for re-contact. Re-contact occurs when the slider’s normal motion becomes equal to the transverse displacement of the disc at the polar coordinate of the slider. And when this happens, a very short-lived impact force is considered to act between the slider and the disc within time duration of \(({t_r^-, t_r^+})\). The method for determining the values of the dynamic state variables immediately after re-contact, which was given in [44], is adopted in this paper.

For simplification, an assumption for the re-contact is that the impact is perfectly plastic and the slider sticks onto the disc after the impact. Suppose the impulse at \(t_r\) is p; thus, the distributed load on the disc due to the impact is \(-p\delta ({r-r_0}) \delta ({\theta -{\varphi }(t)}) \delta ({t-t_r})\), which causes the equations of motion of the disc to become,

$$\begin{aligned}&M_{kl} {\ddot{C}}_{kl} + 2lM_{kl} {\varOmega }{\dot{D}}_{kl} + \left( \omega _{kl}^2 M_{kl}- l^{2} M_{kl} {\varOmega }^{2}\right) C_{kl} \nonumber \\&\quad = - p R_{kl} (r_{0}) \hbox {cos} (l {\varphi }(t)) \delta (t - t_{r})\end{aligned}$$
(45)
$$\begin{aligned}&M_{kl} {\ddot{D}}_{kl} + 2lM_{kl} {\varOmega }{\dot{C}}_{kl} + \left( \omega _{kl}^2 M_{kl}- l^{2} M_{kl} {\varOmega }^{2}\right) D_{kl} \nonumber \\&\quad = - p R_{kl} (r_{0}) \hbox {sin} (l {\varphi }(t)) \delta (t - t_{r}) \end{aligned}$$
(46)

The velocity jump for the disc due to the impact can be thus obtained as,

$$\begin{aligned}&{\dot{C}}_{kl} (t_{r}^{+}) - {\dot{C}}_{kl} (t_{r}^{-}) = - \frac{p R_{kl} (r_{0}) \hbox {cos} (l {\varphi }(t_{r}))}{M_{kl}} \end{aligned}$$
(47)
$$\begin{aligned}&{\dot{D}}_{kl} (t_{r}^{+}) - {\dot{D}}_{kl} (t_{r}^{-}) = - \frac{p R_{kl} (r_{0}) \hbox {sin} (l {\varphi }(t_{r}))}{M_{kl}} \end{aligned}$$
(48)

Similarly, the velocity jump of the slider is,

$$\begin{aligned} {\dot{z}} (t_{r}^{+}) - {\dot{z}} (t_{r}^{-}) = \frac{p}{m} \end{aligned}$$
(49)

Combining Eq. (49) and Eqs. (47) and (48) gives,

$$\begin{aligned}&{\dot{C}}_{kl} (t_{r}^{+}) - {\dot{C}}_{kl} (t_{r}^{-}) \nonumber \\&\quad = - \frac{m R_{kl} (r_{0}) \hbox {cos} (l {\varphi }(t_{r})) [{\dot{z}} (t_{r}^{+}) - {\dot{z}}(t_{r}^{-})]}{M_{kl}} \end{aligned}$$
(50)
$$\begin{aligned}&{\dot{D}}_{kl} (t_{r}^{+}) - {\dot{D}}_{kl} (t_{r}^{-}) \nonumber \\&\quad = - \frac{m R_{kl} (r_{0}) \hbox {sin} (l {\varphi }(t_{r})) [{\dot{z}} (t_{r}^{+}) - {\dot{z}} (t_{r}^{-})]}{M_{kl}} \end{aligned}$$
(51)

For perfectly plastic impact, the slider has the same velocity as that of the disc at time \(t_r^+\); therefore,

$$\begin{aligned} \begin{aligned} {\dot{z}} (t_{r}^{+})&= \left( \frac{\partial w}{\partial t} + {\dot{{\varphi }}} \frac{\partial w}{\partial {\varphi }}\right) _{t = t_{r}^{+}} \\&= \sum \limits _{r=0}^{\infty } \sum \limits _{s=0}^{\infty } R_{rs} (r_{0}) \\&\qquad [\hbox {cos} (s {\varphi }(t_{r}^{+})) {\dot{C}}_{rs} (t_{r}^{+}) \\&\qquad + \hbox {sin} (s {\varphi }(t_{r}^{+})) {\dot{D}}_{rs} (t_{r}^{+}) \\&\qquad - {\dot{{\varphi }}} (t_{r}^{+}) s\hbox {sin} (s {\varphi }(t_{r}^{+})) {C}_{rs} (t_{r}^{+}) \\&\qquad + {\dot{{\varphi }}} (t_{r}^{+}) s\hbox {cos} (s {\varphi }(t_{r}^{+})) {D}_{rs} (t_{r}^{+})] \end{aligned} \end{aligned}$$
(52)

Because the transverse displacement and the in-plane motion of the slider are unchanged by the normal impact, the following equations hold,

$$\begin{aligned} \begin{aligned}&C_{kl} ({t_r^+ }) =C_{kl} ({t_r^- })=C_{kl} ({t_r }), \\&D_{kl} ({t_r^+}) =D_{kl} ({t_r^- })=D_{kl} ({t_r }), \\&{\varphi }({t_r^+ }) ={\varphi }({t_r^-})={\varphi }({t_r }), \\&{\dot{{\varphi }}}({t_r^+}) = {\dot{{\varphi }}} ({t_r^-}) ={\dot{{\varphi }}} ({t_r}) \end{aligned} \end{aligned}$$
(53)

By substituting Eq. (52) into Eqs. (50) and (51) and utilising Eq. (53), the normal velocity of the slider and the modal velocities of the disc after the impact can be derived as,

$$\begin{aligned}&\begin{aligned}&{\dot{z}} (t_{r}^{+}) \\&= \frac{{\sum }_{r=0}^{\infty } {\sum }_{s=0}^{\infty } R_{rs} (r_{0}) \left[ \hbox {cos} (s {\varphi }(t_{r})) {\dot{C}}_{rs} (t_{r}^{-}) + \hbox {sin} (s {\varphi }(t_{r})) {\dot{D}}_{rs} (t_{r}^{-}) + \frac{mR_{rs} (r_{0})}{M_{rs}} {\dot{z}} (t_{r}^{-}) - {\dot{{\varphi }}} (t_{r}) s\hbox {sin} (s {\varphi }(t_{r})) {C}_{rs} (t_{r}) + {\dot{{\varphi }}} (t_{r}) s\hbox {cos} (s {\varphi }(t_{r})) {D}_{rs} (t_{r})\right] }{1+ {\sum }_{r=0}^{\infty } {\sum }_{s=0}^{\infty } \frac{mR_{rs}^{2} (r_{0})}{M_{rs}}} \end{aligned} \end{aligned}$$
(54)
$$\begin{aligned}&\begin{aligned}&{\dot{C}}_{kl} ({t_r^+ }) \\&\quad = {\dot{C}}_{kl} ({t_r^- }) - \frac{m R_{kl} (r_{0}) \hbox {cos} (l {\varphi }(t_{r}))}{M_{kl}} \\&\quad \left\{ \frac{{\sum }_{r=0}^{\infty } {\sum }_{s=0}^{\infty } R_{rs} (r_{0})\left[ \hbox {cos} (s {\varphi }(t_{r})) {\dot{C}}_{rs} (t_{r}^{-}) + \hbox {sin} (s {\varphi }(t_{r})) {\dot{D}}_{rs} (t_{r}^{-}) + \frac{mR_{rs} (r_{0})}{M_{rs}} {\dot{z}} (t_{r}^{-}) - {\dot{{\varphi }}} (t_{r}) s\hbox {sin} (s {\varphi }(t_{r})) {C}_{rs} (t_{r}) + {\dot{{\varphi }}} (t_{r}) s\hbox {cos} (s {\varphi }(t_{r})) {D}_{rs} (t_{r})\right] }{1+ {\sum }_{r=0}^{\infty } {\sum }_{s=0}^{\infty } \frac{mR_{rs}^{2} (r_{0})}{M_{rs}}} - {\dot{z}} (t_{r}^{-}) \right\} \end{aligned} \nonumber \\\end{aligned}$$
(55)
$$\begin{aligned}&\begin{aligned}&{\dot{D}}_{kl} ({t_r^+ }) \\&\quad = {\dot{D}}_{kl} ({t_r^- }) - \frac{m R_{kl} (r_{0}) \hbox {sin} (l {\varphi }(t_{r}))}{M_{kl}} \\&\quad \left\{ \frac{{\sum }_{r=0}^{\infty } {\sum }_{s=0}^{\infty } R_{rs} (r_{0}) [\hbox {cos} (s {\varphi }(t_{r})) {\dot{C}}_{rs} (t_{r}^{-}) + \hbox {sin} (s {\varphi }(t_{r})) {\dot{D}}_{rs} (t_{r}^{-}) + \frac{mR_{rs} (r_{0})}{M_{rs}} {\dot{z}} (t_{r}^{-}) - {\dot{{\varphi }}} (t_{r}) s\hbox {sin} (s {\varphi }(t_{r})) {C}_{rs} (t_{r}) + {\dot{{\varphi }}} (t_{r}) s\hbox {cos} (s {\varphi }(t_{r})) {D}_{rs} (t_{r})]}{1+ {\sum }_{r=0}^{\infty } {\sum }_{s=0}^{\infty } \frac{mR_{rs}^{2} (r_{0})}{M_{rs}}} - {\dot{z}} (t_{r}^{-}) \right\} \end{aligned}\nonumber \\ \end{aligned}$$
(56)
Table 1 The values of the constant system parameters
Full size table

3 Numerical simulation and analysis

Because there are three distinct dynamic phases with different governing equations of motion throughout the process of vibration, the dynamic system in question is non-smooth, which brings about a difficulty in numerical calculation. To obtain the whole time histories of the dynamic responses of the system, Runge–Kutta method [45] suitable for the second-order ordinary differential equations is employed to obtain the responses in every single phase while conditions for phase transitions are monitored at each time step. Within the time step in which a phase transition happens, the bisection method is used to capture the exact transition time instant. After the transition point, the phase changes and the original set of equations of motion is replaced by another one. In the following, the dynamic behaviours of the frictional system in the three situations of spinning speed of disc are investigated and relevant interesting phenomena are analysed.

Fig. 3
figure 3

Combinations of \(c_z\) and \(r_0^2 c_{\varphi }\) corresponding to stable sliding equilibrium with different values of \(\alpha \) under two spinning speeds: a\({\varOmega }_{\mathrm{c}} =1\,\hbox {rad}/\hbox {s}\), b\({\varOmega }_{\mathrm{c}} = 10 \, \hbox {rad}/\hbox {s}\). ‘stable’ refers to the region above the respective curve

Full size image

The basic system parameters whose values are constant in the numerical examples are listed in Table 1. It should be noted that numbers k and l in the expression of the transverse displacement of the disc can be chosen to include as many modes as needed to represent the dynamics of the system with acceptable accuracy. To avoid excessive computations, the modal series in Eq. (24) are truncated at suitable values of indices k and l. The first seven natural frequencies of the disc are 1492, 1517, 1517, 1824, 1824, 2774 and 2774 rad/s, which are 237, 241, 241, 290, 290, 442 and 442 in Hz. It is found that the first seven disc modes (one single mode with zero nodal circle and zero nodal diameter and three pairs of doublet modes with zero nodal circle and one, two or three nodal diameters) are good enough in terms of the convergence of the results.

3.1 Stable sliding equilibrium under the constant speed and the effects of time-variant speed

In this subsection, the dynamic responses in the three different situations of disc speed are obtained and compared to reveal the effects of time-variant disc speed on the friction-induced dynamics of the system.

In the situation of constant disc speed, it is viable to find an equilibrium point in the slip state for the system by solving the algebraic nonlinear equations obtained by setting all the terms involving velocity and acceleration in Eqs. (33), (34) and (36) to be zero. The algebraic nonlinear equations to determine the equilibrium point are solved numerically using fsolve in MATLAB. Then, the Lyapunov stability at this equilibrium point is investigated. That is, if the solutions of Eqs. (33), (34) and (36) with a small initial perturbation from the equilibrium point converge to the equilibrium point with time approaching infinity, the sliding equilibrium under study is considered to be asymptotically stable; while if the solutions move away from the equilibrium point with time increasing, the sliding equilibrium under study is unstable. Based on the system parameters listed in Table 1, the regions of stability with respect to four parameters \(c_z\), \(c_{\varphi }\), \(\alpha \) and \({\varOmega }_{\mathrm{c}}\) which are found to have significant effects on the stability are obtained. Figure 3 illustrates some combinations of \(c_z\) and \(r_0^2 c_{\varphi }\) which correspond to stable sliding equilibriums with different values of \(\alpha \) under two different constant spinning speeds \({\varOmega }_{\mathrm{c}} =1\) and \(10\, \hbox {rad}/\hbox {s}\).

Fig. 4
figure 4

The system dynamic responses under the constant disc speed: a the circumferential velocity of the slider, b the transverse displacement of a specific point on the disc at \(r=r_0\) and \(\theta =0\) (\(c_z =11 \, \hbox {N}\, \hbox {s}/\hbox {m}\), \(r_0^2 c_{\varphi }=1 \, \hbox {N}\,\hbox {m}\, \hbox {s}/\hbox {rad}\), \(\alpha =10\), \({\varOmega }_{\mathrm{c}} =10\, \hbox {rad}/\hbox {s}\))

Full size image
Fig. 5
figure 5

The system dynamic responses under the decelerating disc: a the circumferential velocity of the slider, b the transverse displacement of a specific point on the disc at \(r=r_0 \) and \(\theta =0\) (\(c_z =11 \, \hbox {N}\, \hbox {s}/\hbox {m}\), \(r_0^2 c_{\varphi }=1 \, \hbox {N}\,\hbox {m}\, \hbox {s}/\hbox {rad}\), \(\alpha =10\), \({\varOmega }_{\mathrm{0}} =10\, \hbox {rad}/\hbox {s}\), \(t_{\mathrm{max}} =20\,\hbox {s}\))

Full size image
Fig. 6
figure 6

The system dynamic responses under the constant disc speed: a the circumferential velocity of the slider, b the transverse displacement of a specific point on the disc at \(r=r_0 \) and \(\theta =0\) (\(c_z =1\,\hbox {N}\,\hbox {s}/\hbox {m}\), \(r_0^2 c_{\varphi }=2 \, \hbox {N}\,\hbox {m}\,\hbox {s}/\hbox {rad}\), \(\alpha =0\), \({\varOmega }_{\mathrm{c}} =1\,\hbox {rad}/\hbox {s})\)

Full size image
Fig. 7
figure 7

The system dynamic responses under the accelerating disc: a the circumferential velocity of the slider, b the transverse displacement of a specific point on the disc at \(r=r_0 \) and \(\theta =0\) (\(c_z =1\,\hbox {N}\,\hbox {s}/\hbox {m}\), \(r_0^2 c_{\varphi }=2 \, \hbox {N}\,\hbox {m}\, \hbox {s}/\hbox {rad}\), \(\alpha =0\), \({\varOmega }_{\mathrm{1}} =1\,\hbox {rad}/\hbox {s}\), \(c=3\,\hbox {rad}/\hbox {s}^{2}\))

Full size image

Considering a parameter combination in the ‘stable’ area (\(c_z =11 \, \hbox {N}\, \hbox {s}/\hbox {m}\), \(r_0^2 c_{\varphi }=1 \, \hbox {N}\,\hbox {m}\,\hbox {s}/\hbox {rad}\), \(\alpha =10\), \({\varOmega }_{\mathrm{c}} =10 \, \hbox {rad}/\hbox {s}\)), it can be seen from Fig. 4 that the amplitudes of dynamic responses of the system decay fast with time until the sliding equilibrium is reached. For comparison, the vibration in the situation of decelerating disc (\({\varOmega }_{\mathrm{0}} =10 \, \hbox {rad}/\hbox {s}\), \(t_{\mathrm{max}} =20 \, \hbox {s}\)) with the same parameter values and initial condition as those in the situation of constant disc speed is investigated and the results are depicted in Fig. 5. An interesting phenomenon arises that the vibration decays in the early stage, similarly to that in the situation of constant speed, but then grows in the final stage and the stick–slip motion is induced. The reason for this phenomenon is the negative slope of the friction force–relative velocity relationship, which is usually considered a contributor to system instability. With the decrease in disc speed, the magnitude of the relative velocity \(|{{\varOmega }- {\dot{{\varphi }}}}|\) can become sufficiently low (please note that \({\dot{{\varphi }}}\) becomes approximately zero before the vibration grows in the end of the process), leading to a large negative slope of the friction force–relative velocity dependence, which, acting like a negative damping, can cancel out the positive viscous damping and then cause the vibration of the system to grow towards the end of the decelerative process. A similar phenomenon can occur in the situation of accelerating disc, but the mechanism is different. Another parameter combination which also leads to a stable sliding equilibrium in the situation of constant disc speed (\(c_z =1 \, \hbox {N}\,\hbox {s}/\hbox {m}\), \(r_0^2 c_{\varphi }=2 \, \hbox {N}\, \hbox {m}\,\hbox {s}/\hbox {rad}\), \(\alpha = 0\), \({\varOmega }_{\mathrm{c}} =1 \, \hbox {rad}/\hbox {s}\)) is used. The time histories of responses starting from a small perturbation from the sliding equilibrium under the constant disc speed are shown in Fig. 6. Similarly, the vibration decays fast until the sliding equilibrium is reached. Meanwhile, the system responses in the situation of accelerating disc (\({\varOmega }_{\mathrm{1}} =1 \, \hbox {rad}/\hbox {s}, =3 \, \hbox {rad}/\hbox {s}^{2}\)) with the same parameter values and initial condition as those in the situation of constant disc speed are obtained and plotted in Fig. 7. As shown in this figure, the vibration decays at first but starts to grow at a time point later due to the increase of disc speed. This phenomenon can be explained by the effect of moving load which causes speed-dependent instability [27, 29]. The two examples above reflect the time-varying characteristics of the friction-induced vibration of the system due to the time-variant disc speed.

Fig. 8
figure 8

The time history of the circumferential angular velocity of the slider and time–frequency plot of the circumferential angular displacement of the slider under the constant disc speed: a the time history of the circumferential angular velocity, b the time–frequency plot of the circumferential angular displacement (\(c_z =0.1\,\hbox {N}\, \hbox {s}/\hbox {m}\), \(r_0^2 c_{\varphi }=0.1 \, \hbox {N}\, \hbox {m}\, \hbox {s}/\hbox {rad}\), \(\alpha =1\), \({\varOmega }_{\mathrm{c}} =2\pi \, \hbox {rad}/\hbox {s})\)

Full size image
Fig. 9
figure 9

The time history and time–frequency plot of the transverse displacement of the disc at \(r=r_0\) and \(\theta =1\,\hbox {rad}\) under the constant disc speed: a the time history, b the frequency spectrum plot

Full size image
Fig. 10
figure 10

The time history of the circumferential angular velocity of the slider and time–frequency plot of the circumferential angular displacement of the slider under the decelerating disc: a the time history of the circumferential angular velocity, b the time–frequency plot of the circumferential angular displacement (\(c_z =0.1\,\hbox {N}\, \hbox {s}/\hbox {m}\), \(r_0^2 c_{\varphi }=0.1 \, \hbox {N}\,\hbox {m}\, \hbox {s}/\hbox {rad}\), \(\alpha =1\), \({\varOmega }_{\mathrm{0}} =2 \pi \, \hbox {rad}/\hbox {s}\), \(t_{\mathrm{max}} =35\,\hbox {s}\))

Full size image
Fig. 11
figure 11

The time history and time–frequency plot of the transverse displacement of the disc at \(r=r_0\) and \(\theta =1\,\hbox {rad}\) under the decelerating disc: a the time history, b the frequency spectrum plot

Full size image

3.2 Non-stationary dynamic behaviour under the time-variant disc speed

Next, the parameter combinations corresponding to unstable sliding equilibrium in the situation of constant disc speed are considered and the dynamic responses in the three situations of disc speed are compared. The initial displacements and velocities are set to be zero in all the numerical examples below. The parameter values used in the first example are: \(c_z =0.1\,\hbox {N}\, \hbox {s}/\hbox {m}\), \(r_0^2 c_{\varphi }=0.1 \, \hbox {N}\,\hbox {m}\, \hbox {s}/\hbox {rad}\), \(\alpha =1\) and \({\varOmega }_{\mathrm{c}} =2 \pi \, \hbox {rad}/\hbox {s}\) in the situation of constant speed. The results about the in-plane angular motion of the slider and the transverse vibration of the disc under the constant disc speed are illustrated in Figs. 8 and 9, respectively. In these figures, the time–frequency plots are obtained from the short-time Fourier transform, from which it can be observed that the frequency compositions of the responses remain unchanged throughout the whole process, indicating that the dynamic responses are stationary. Besides, both the frequency spectra of the in-plane angular motion of the slider and the transverse vibration of the disc consist of several incommensurate frequencies and two common incommensurate frequencies \(f_1 =181\) Hz and \(f_2 =290.5\) Hz can be identified, which suggests that both dynamic responses are quasi-periodic. The vibration of the system in the situation of decelerating disc is then investigated and the results concerning the in-plane angular motion of the slider and the transverse vibration of the disc are illustrated in Figs. 10 and 11. The time–frequency plots show the time-variant characteristic of frequency spectra of the responses, especially the in-plane motion of the slider, in the situation of decelerating disc. In the early stage of vibration, the frequency spectra of responses are similar to those in the situation of constant speed, but lower-frequency components arise in the dynamic responses towards the end of the process, and the frequency spectrum of the in-plane motion of the slider gets very fuzzy and dense in the final stage of the process. The variation of the frequencies of the response during the process can also be observed from the time histories during two different time spans in the early and late stages, as depicted in Fig. 12.

Fig. 12
figure 12

The short-term time histories during two different time spans under the decelerating disc: a, b the circumferential angular velocity of the slider, c, d the friction force

Full size image
Fig. 13
figure 13

The time history of the circumferential angular velocity of the slider and time–frequency plot of the circumferential angular displacement of the slider under the constant disc speed: a the time history of the circumferential angular velocity, b the time–frequency plot of the circumferential angular displacement (\(c_z =2\,\hbox {N}\, \hbox {s}/\hbox {m}\), \(r_0^2 c_{\varphi }=0.5 \, \hbox {N}\,\hbox {m}\, \hbox {s}/\hbox {rad}\), \(\alpha =1\), \({\varOmega }_{\mathrm{c}} =2 \pi \, \hbox {rad}/\hbox {s}\))

Full size image
Fig. 14
figure 14

The time history and time–frequency plot of the transverse displacement of the disc at \(r=r_0\) and \(\theta =1\,\hbox {rad}\) under the constant disc speed: a the time history, b the frequency spectrum plot

Full size image
Fig. 15
figure 15

The time history of the circumferential angular velocity of the slider and time–frequency plot of the circumferential angular displacement of the slider under the decelerating disc: a the time history of the circumferential angular velocity, b the time–frequency plot of the circumferential angular displacement (\(c_z =2\,\hbox {N}\, \hbox {s}/\hbox {m}\), \(r_0^2 c_{\varphi }=0.5 \, \hbox {N}\, \hbox {m}\, \hbox {s}/\hbox {rad}\), \(\alpha =1\), \({\varOmega }_{\mathrm{0}} =2 \pi \, \hbox {rad}/\hbox {s}\), \(t_{\mathrm{max}} =35\,\hbox {s}\))

Full size image
Fig. 16
figure 16

The time history and time–frequency plot of the transverse displacement of the disc at \(r=r_0\) and \(\theta =1\,\hbox {rad}\) under the decelerating disc: a the time history, b the frequency spectrum plot

Full size image
Fig. 17
figure 17

The phase portraits of the circumferential motion of the slider and trajectories of friction force during short-term time spans within six different time segments under the decelerating disc: a, b\(5<t<5.1\,\hbox {s}\), c, d\(12<t<12.1\,\hbox {s}\), e, f\(20<t<20.1\,\hbox {s}\), g, h\(26<t<26.1\,\hbox {s}\), i, j\(29<t<29.1\,\hbox {s}\), k, l\(33<t<35\,\hbox {s}\)

Full size image

The second example uses the parameter values: \(c_z =2\,\hbox {N}\, \hbox {s}/\hbox {m}\), \(r_0^2 c_{\varphi }=0.5 \, \hbox {N}\, \hbox {m}\,\hbox {s}/\hbox {rad}\), \(\alpha =1\) and \({\varOmega }_{\mathrm{c}} =2 \pi \, \hbox {rad}/\hbox {s}\) in the situation of constant speed. Figures 13 and 14 illustrate the time histories and time–frequency plots of the in-plane motion of the slider and transverse vibration of the disc. The frequency compositions of the responses remain unchanged, and both the frequency spectra of the in-plane angular displacement of the slider and the transverse displacement of the disc consist of the fundamental frequency \(f_0 \, (206 \, \hbox {Hz})\) and its superharmonics (\(nf_o ,n=2,3,\dots \)), indicating that the in-plane motion of the slider and the transverse motion of the disc are periodic at the same frequency. Correspondingly, the results of the dynamic responses in the situation of decelerating disc are illustrated in Figs. 15 and 16. As shown in Fig. 15b, at least six segments with distinct frequency compositions, which are in time intervals \(0<t<10\,\hbox {s}\), \(10<t<15\,\hbox {s}\), \(15<t<25\,\hbox {s}\), \(25<t<28\,\hbox {s}\), \(28<t<30\,\hbox {s}\), \(30<t<35\,\hbox {s}\), can be identified based on visual inspection. The phase portraits of the circumferential motion of the slider and trajectories of the friction force during certain time spans in the six segments are shown in Fig. 17. As is seen, stick–slip vibration with different periods in the six time intervals can be identified for the in-plane motion of the slider.

Fig. 18
figure 18

The variation of normal force with time in the situation of constant speed in the two cases: a\(c_z =0.1\,\hbox {N}\,\hbox {s}/\hbox {m}\), \(r_0^2 c_{\varphi }=0.1\, \hbox {N}\,\hbox {m}\,\hbox {s}/\hbox {rad}\), \(\alpha =1\), \({\varOmega }_{\mathrm{c}} =6 \pi \, \hbox {rad}/\hbox {s}\), b\(c_z =2\,\hbox {N}\,\hbox {s}/\hbox {m}\), \(r_0^2 c_{\varphi }=0.5 \, \hbox {N}\,\hbox {m}\, \hbox {s}/\hbox {rad}\), \(\alpha =1\), \({\varOmega }_{\mathrm{c}} =6 \pi \, \hbox {rad}/\hbox {s}\)

Full size image
Fig. 19
figure 19

The variation of normal force with time in the situation of deceleration in the two cases: a\(c_z =0.1\,\hbox {N}\, \hbox {s}/\hbox {m}\), \(r_0^2 c_{\varphi }=0.1 \, \hbox {N}\, \hbox {m}\, \hbox {s}/\hbox {rad}\), \(\alpha =1\), \({\varOmega }_{\mathrm{0}} =6 \pi \, \hbox {rad}/\hbox {s}\), \(t_{\mathrm{max}} =35\,\hbox {s}\), b\(c_z =2\,\hbox {N}\, \hbox {s}/\hbox {m}\), \(r_0^2 c_{\varphi }=0.5 \, \hbox {N}\, \hbox {m}\, \hbox {s}/\hbox {rad}\), \(\alpha =1\), \({\varOmega }_{\mathrm{0}} =6 \pi \, \hbox {rad}/\hbox {s}\), \(t_{\mathrm{max}} =35\,\hbox {s}\)

Full size image
Fig. 20
figure 20

The time histories and time–frequency plots of the dynamic responses under the constant speed: a, b the in-plane motion of the slider, c, d the transverse motion of the disc. (\(c_z =0.1\,\hbox {N}\, \hbox {s}/\hbox {m}\), \(r_0^2 c_{\varphi }=0.1 \, \hbox {N}\, \hbox {m}\, \hbox {s}/\hbox {rad}\), \(\alpha =1\), \({\varOmega }_{\mathrm{c}} =6 \pi \, \hbox {rad}/\hbox {s}\))

Full size image
Fig. 21
figure 21

The time histories and time–frequency plots of the dynamic responses under the constant speed: a, b the in-plane motion of the slider, c, d the transverse motion of the disc. (\(c_z =2\,\hbox {N}\, \hbox {s}/\hbox {m}\), \(r_0^2 c_{\varphi }=0.5 \, \hbox {N}\, \hbox {m}\, \hbox {s}/\hbox {rad}\), \(\alpha =1\), \({\varOmega }_{\mathrm{c}} =6 \pi \, \hbox {rad}/\hbox {s}\))

Full size image
Fig. 22
figure 22

The time histories and time–frequency plots of the dynamic responses under the decelerating disc: a, b the in-plane motion of the slider, c, d the transverse motion of the disc. (\(c_z =0.1\,\hbox {N}\, \hbox {s}/\hbox {m}\), \(r_0^2 c_{\varphi }=0.1\, \hbox {N}\, \hbox {m}\, \hbox {s}/\hbox {rad}\), \(\alpha =1\), \({\varOmega }_{\mathrm{0}} =6 \pi \, \hbox {rad}/\hbox {s}\), \(t_{\mathrm{max}} =35\,\hbox {s}\))

Full size image
Fig. 23
figure 23

The time histories and time–frequency plots of the dynamic responses under the decelerating disc: a, b the in-plane motion of the slider, c, d the transverse motion of the disc. (\(c_z =2\,\hbox {N}\, \hbox {s}/\hbox {m}\), \(r_0^2 c_{\varphi }=0.5 \, \hbox {N}\, \hbox {m}\, \hbox {s}/\hbox {rad}\), \(\alpha =1\), \({\varOmega }_{\mathrm{0}} =6 \pi \, \hbox {rad}/\hbox {s}\), \(t_{\mathrm{max}} =35\,\hbox {s}\))

Full size image

The cases with the same parameter combinations in the examples above but at a larger disc speed \({\varOmega }_{\mathrm{c}} \, (6 \pi \, \hbox {rad}/\hbox {s})\) in the situation of constant disc speed are then considered. It is found that separation happens in both cases, as depicted in Fig. 18, where the normal contact force is zero during separation. For comparison, the variation of normal force with time in the situation of decelerating disc is illustrated in Fig. 19. Besides, the in-plane motions of the slider and the transverse motions of the disc under the constant disc speed in the two cases are illustrated in Figs. 20 and 21, respectively. The corresponding results in the situation of decelerating disc are shown in Figs. 22 and 23, respectively. Similarly, the frequency spectra of responses in the situation of decelerating disc are more time variant than those in the situation of constant disc speed. It is also observed that lower-frequency components arise in the dynamic responses and the frequency spectra get fuzzy and dense towards the end of the process in Fig. 23b, while this feature is not seen in Fig. 22b. The reason is that there is no separation in the late stage of the decelerative process in the second case, while in the first case, separation and re-contact occur throughout the whole decelerative process, as shown in Fig. 19.

Fig. 24
figure 24

The variation of normal force with time in the situation of accelerating disc in the two cases: a\(c_z =0.1\,\hbox {N}\, \hbox {s}/\hbox {m}\), \(r_0^2 c_{\varphi }=0.1 \, \hbox {N}\, \hbox {m}\, \hbox {s}/\hbox {rad}\), \(\alpha =1\), \({\varOmega }_{\mathrm{1}} =2 \pi \, \hbox {rad}/\hbox {s}\), \(c=0.2\,\hbox {rad}/\hbox {s}^{2}\), b\(c_z =2\,\hbox {N}\, \hbox {s}/\hbox {m}\), \(r_0^2 c_{\varphi }=0.5 \, \hbox {N}\, \hbox {m}\, \hbox {s}/\hbox {rad}\), \(\alpha =1\), \({\varOmega }_{\mathrm{1}} =2 \pi \, \hbox {rad}/\hbox {s}\), \(c=0.2\,\hbox {rad}/\hbox {s}^{2}\)

Full size image
Fig. 25
figure 25

The time histories and time–frequency plots of the dynamic responses under the accelerating disc: a, b the in-plane motion of the slider, c, d the transverse motion of the disc. (\(c_z =0.1\,\hbox {N}\, \hbox {s}/\hbox {m}\), \(r_0^2 c_{\varphi }=0.1 \, \hbox {N}\, \hbox {m}\, \hbox {s}/\hbox {rad}\), \(\alpha =1\), \({\varOmega }_{\mathrm{1}} =2 \pi \, \hbox {rad}/\hbox {s}\), \(c=0.2\,\hbox {rad}/\hbox {s}^{2}\))

Full size image

The effect of accelerating disc on the system dynamics is also investigated. The variations of normal force are plotted in Fig. 24, from which it is seen that separation happens with the increase of disc speed in the process, while there is no separation occurring for the corresponding system in the situation of constant disc speed. The dynamic responses under the accelerating disc are illustrated in Figs. 25 and 26. It is noticed that separation happening in the process leads to shift of frequency spectra of the system responses.

Fig. 26
figure 26

The time histories and time–frequency plots of the dynamic responses under the accelerating disc: a, b the in-plane motion of the slider, c, d the transverse motion of the disc. (\(c_z =2\,\hbox {N}\, \hbox {s}/\hbox {m}\), \(r_0^2 c_{\varphi }=0.5\, \hbox {N}\, \hbox {m}\, \hbox {s}/\hbox {rad}\), \(\alpha =1\), \({\varOmega }_{\mathrm{1}} =2 \pi \, \hbox {rad}/\hbox {s}\), \(c=0.2\,\hbox {rad}/\hbox {s}^{2}\))

Full size image

3.3 Separation and impact during vibration

As the amplitude of transverse vibration of the disc increases, the slider may separate from the disc and then re-contact with disc. In the situation of constant disc speed, whether separation occurs in the vibration is only dependent on the magnitude of the spinning speed for a given combination of system parameters [31, 33], while in the situation of decelerating disc, the initial spinning speed \({\varOmega }_0\) and the time length of the decelerative process \(t_{\mathrm{max}}\) are two important factors on the onset of separation phenomenon. The separation region with respect to \({\varOmega }_0\) and \(t_{\mathrm{max}}\) with one of the parameter combinations in the examples above is shown in Fig. 27. (The initial displacements and velocities are zero.) It can be seen that separation is more likely to happen in the case of high initial speed and long decelerative process in the situation of decelerating disc. In the situation of accelerating disc, separation can always happen with the increase of spinning speed of disc.

Fig. 27
figure 27

The separation region (SR) with respect to \({\varOmega }_0\) and \(t_{\mathrm{max}}\) in the situation of decelerating disc (\(c_z =0.1\,\hbox {N}\, \hbox {s}/\hbox {m}\), \(r_0^2 c_{\varphi }=0.1 \, \hbox {N}\, \hbox {m}\, \hbox {s}/\hbox {rad}\), \(\alpha =1\))

Full size image

The role of the impact happening at the instants of re-contact on the system dynamics is examined. The dynamic responses of the system under the constant disc speed in two conditions: with impact and without impact, are obtained to exemplify the effect of the impact on the vibration. When the impact is ignored, the transverse velocity of the disc is not changed during the re-contact. Figure 28 shows the time histories of the transverse displacement at \((r_0 ,0)\) of the disc with a certain parameter combinations. It is seen that the transverse vibration with impact considered is much weaker compared with that without impact, which can be explained by the fact that the impact is assumed to be fully plastic in this paper and thus dissipates energy in the vibration.

Fig. 28
figure 28

The time histories of the transverse displacement in the situation of constant disc speed under two conditions: a with impact, b without impact (\(c_z =0\), \(r_0^2 c_{\varphi }=0\), \(\alpha =1\), \({\varOmega }_{\mathrm{c}} =50\,\hbox {rad}/\hbox {s}\))

Full size image

4 Conclusions

In this work, the dynamics of a slider-on-disc system subject to friction force in three different situations of spinning speed, i.e. constant deceleration, constant acceleration and constant speed, is investigated. Due to the non-smooth nature of the friction force between the slider and the disc, the slider experiences stick–slip vibration in the circumferential direction of the disc. Meanwhile, the in-plane motion of the slider causes time-varying normal force and bending moment on the disc, which can be seen as moving loads to excite the transverse vibration of the elastic disc. The transverse vibration of the disc will, in turn, influence the in-plane motion of the slider by affecting the magnitude of friction force through the varying normal force. Therefore, the transverse vibration and the in-plane vibration of the slider are coupled. It is observed the decelerating and accelerating disc rotation results in distinct dynamic behaviours of the frictional system from that under the constant disc speed. The following conclusions can be reached,

  1. 1.

    In the situation of constant speed, a sliding equilibrium of the system can be found. The parameter combinations corresponding to the stable or unstable equilibrium points in the sense of Lyapunov stability are identified.

  2. 2.

    For the system with the parameter combinations corresponding to the stable sliding equilibrium in the situation of constant speed, the vibration starting from an initial condition near the equilibrium point decays with time and ceases eventually, while in the situation of time-varying disc speed, stability may change with time due to the variation of disc speed with time, resulting in an interesting phenomenon that the system vibration decays with time in the early stage but grows in the later stage. This kind of time-varying characteristic of friction-induced vibration results from the negative-slope friction force–relative velocity relationship in the situation of decelerating disc and the speed-dependent instability caused by the moving load in the situation of accelerating disc.

  3. 3.

    The time-variant disc speed increases the non-stationary characteristics of the system dynamics as opposed to the constant disc speed, especially the in-plane motion of the slider, which means there are more shifts of frequency spectra of the dynamic responses throughout the process in the situation of time-variant disc speed than that in the situation of constant speed.

  4. 4.

    In the situation of decelerating disc, separation is more inclined to happen in the case of high initial disc speed and long decelerating process. When impact is considered, the transverse vibration of the disc becomes lower than without.