Skip to main content
SpringerLink
Log in

Rational and semi-rational solutions of the modified Kadomtsev–Petviashvili equation and the \(\varvec{(2 + 1)}\)-dimensional Konopelchenko–Dubrovsky equation

  • Original paper
  • Published:
Nonlinear Dynamics Aims and scope Submit manuscript

Abstract

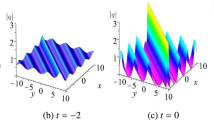
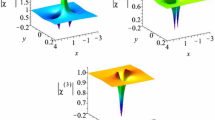
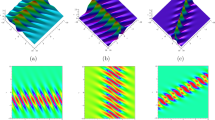
General rational and semi-rational solutions of the modified Kadomtsev–Petviashvili (mKP) equation and the Konopelchenko–Dubrovsky equation are obtained based on the bilinear method and the KP hierarchy reduction technique. These solutions are expressed in terms of \(N \times N\) determinants. The dynamics of the solutions, which exhibit various patterns, are thoroughly analyzed. It is shown that the rational solutions may describe the elastic interaction of a single-peak wave with either a double-peak (M-shape) wave or another single-peak wave for \(N=1\). Depending on the choice of parameters, the semi-rational solutions are found to depict the inelastic interaction between two (Y-shape) or three waves for \(N=1\). The second-order (\(N=2\)) rational solutions exhibit the elastic interaction of three single-peak waves with either one double-peak wave or another single-peak wave. Inelastic interaction is displayed by proper choices of the parameters for semi-rational solutions. When \(N > 2\), similar local dynamical behaviors of the rational and semi-rational solutions have been observed.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12

Similar content being viewed by others

References

  1. Ablowitz, M., Segur, H.: Solitons and the Inverse Scattering Transform. SIAM, University City (1981)

    Book  MATH  Google Scholar 

  2. Ablowitz, M.J., Baldwin, D.E.: Nonlinear shallow ocean-wave soliton interactions on flat beaches. Phys. Rev. E 86(3), 036305 (2012)

    Article  Google Scholar 

  3. Ablowitz, M.J., Ladik, J.F.: A nonlinear difference scheme and inverse scattering. Stud. Appl. Math. 55(3), 213–229 (1976)

    Article  MathSciNet  MATH  Google Scholar 

  4. Ablowitz, M.J., Ladik, J.F.: Nonlinear differential–difference equations and Fourier analysis. J. Math. Phys. 17(6), 1011–1018 (1976)

    Article  MathSciNet  MATH  Google Scholar 

  5. Benney, D.J., Newell, A.C.: The propagation of nonlinear wave envelopes. J. Math. Phys. 46(1–4), 133–139 (1967)

    Article  MathSciNet  MATH  Google Scholar 

  6. Chen, J.C., Chen, Y., Feng, B.F., Maruno, K.: Rational solutions to two-and one-dimensional multicomponent Yajima–Oikawa systems. Phy. Lett. A 379(24–25), 1510–1519 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  7. Cheng, Y., Li, Y.S.: Constraints of the \(2+ 1\) dimensional integrable soliton systems. J. Phys. A 25(2), 419–431 (1992)

    Article  MathSciNet  MATH  Google Scholar 

  8. Estévez, P.G., Gordoa, P.R.: Darboux transformations via Painlevé analysis. Inverse Probl. 13(4), 939 (1997)

    Article  MATH  Google Scholar 

  9. Feng, B.F.: General N-soliton solution to a vector nonlinear Schrödinger equation. J. Phys. A: Math. Theor. 47(35), 355203 (2014)

    Article  MATH  Google Scholar 

  10. Feng, B.F., Luo, X.D., Ablowitz, M.J., Musslimani, Z.H.: General soliton solution to a nonlocal nonlinear Schrödinger equation with zero and nonzero boundary conditions. Nonlinearity 31(12), 5385–5409 (2018)

    Article  MathSciNet  MATH  Google Scholar 

  11. Gu, C.H., Hu, H.S., Zhou, Z.X.: Darboux Transformations in Integrable Systems. Springer, Berlin (2005)

    Book  MATH  Google Scholar 

  12. Hao, H.H., Zhang, D.J.: Soliton resonances for the modified Kadomtsev–Petviashvili equations in uniform and non-uniform media. Modern Phys. Lett. B 24(03), 277–288 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  13. Hirota, R.: Classical Boussinesq equation is a reduction of the modified KP equation. J. Phys. Soc. Jpn. 54(7), 2409–2415 (1985)

    Article  MathSciNet  Google Scholar 

  14. Hirota, R.: The Direct Method in Soliton Theory. Cambridge University Press, Cambridge (2004)

    Book  MATH  Google Scholar 

  15. Hu, X.B., Clarkson, P.A.: Rational solutions of a differential–difference KdV equation, the Toda equation and the discrete KdV equation. J. Phys. A: Math. Gen. 28(17), 5009–5016 (1995)

    Article  MathSciNet  MATH  Google Scholar 

  16. Jimbo, M., Miwa, T.: Solitons and infinite-dimensional Lie algebras. Publ. Res. Inst. Math. Sci. 19(3), 943–1001 (1983)

    Article  MathSciNet  MATH  Google Scholar 

  17. Konopelchenko, B.G.: On the gauge-invariant description of the evolution equations integrable by Gelfand–Dikij spectral problems. Phys. Lett. A 92(7), 323–327 (1982)

    Article  MathSciNet  Google Scholar 

  18. Konopelchenko, B.G., Dubrovsky, V.G.: Some new integrable nonlinear evolution equations in \(2 + 1\) dimensions. Phys. Lett. A 102(1), 15–17 (1984)

    Article  MathSciNet  Google Scholar 

  19. Korteweg, D.J., de Vries, G.: On the change of form of long waves advancing in a rectangular canal, and on a new type of long stationary waves. Philos. Mag. Ser. 39(240), 422–443 (1895)

    Article  MathSciNet  MATH  Google Scholar 

  20. Kumar, M., Kumar, A., Kumar, R.: Similarity solutions of the Konopelchenko–Dubrovsky system using lie group theory. Comput. Math. Appl. 71(10), 2051–2059 (2016)

    Article  MathSciNet  Google Scholar 

  21. Li, M., Hu, W.K., Wu, C.F.: Rational solutions of the classical Boussinesq–Burgers system. Nonlinear Dyn. 94(2), 1291–1302 (2018)

    Article  Google Scholar 

  22. Liu, W., Li, X.L.: General soliton solutions to a \((2+1)\)-dimensional nonlocal nonlinear Schrödinger equation with zero and nonzero boundary conditions. Nonlinear Dyn. 93, 721–731 (2018)

    Article  MATH  Google Scholar 

  23. Liu, W.H., Zhang, Y.F., Shi, D.D.: Lump waves, solitary waves and interaction phenomena to the \((2+1)\)-dimensional Konopelchenko–Dubrovsky equation. Phys. Lett. A 383(2), 97–102 (2019)

    Article  MathSciNet  Google Scholar 

  24. Matveev, V.B., Salle, M.A.: Darboux Transformations and Solitons. Springer Series in Nonlinear Dynamics. Springer, Berlin (1991)

    Book  MATH  Google Scholar 

  25. Miles, J.W.: Obliquely interacting solitary waves. J. Fluid Mech. 79(1), 157–169 (1977)

    Article  MATH  Google Scholar 

  26. Miles, J.W.: Resonantly interacting solitary waves. J. Fluid Mech. 79(1), 171–179 (1977)

    Article  MATH  Google Scholar 

  27. Mu, G., Qin, Z.Y.: Two spatial dimensional N-rogue waves and their dynamics in Mel’nikov equation. Nonlinear Anal. Real World Appl. 18, 1–13 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  28. Ohta, Y., Wang, D.S., Yang, J.K.: General N-dark–dark solitons in the coupled nonlinear Schrödinger equations. Stud. Appl. Math. 127(4), 345–371 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  29. Ohta, Y., Yang, J.K.: General high-order rogue waves and their dynamics in the nonlinear Schrödinger equation. Proc. R. Soc. Lond. Ser. A Math. Phys. Eng. Sci 468(2142), 1716–1740 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  30. Ohta, Y., Yang, J.K.: Rogue waves in the Davey–Stewartson I equation. Phys. Rev. E 86, 036604 (2012)

    Article  Google Scholar 

  31. Ohta, Y., Yang, J.K.: Dynamics of rogue waves in the Davey–Stewartson II equation. J. Phys. A 46(10), 105202, 19 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  32. Ohta, Y., Yang, J.K.: General rogue waves in the focusing and defocusing Ablowitz–Ladik equations. J. Phys. A 47(25), 255201, 23 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  33. O’Keir, I.S., Parkes, E.J.: The derivation of a modified Kadomtsev–Petviashvili equation and the stability of its solutions. Phys. Scr. 55(2), 135–142 (1997)

    Article  Google Scholar 

  34. Rao, J.G., Porsezian, K., He, J.S.: Semi-rational solutions of the third-type Davey–Stewartson equation. Chaos 27(8), 083115 (2017)

    Article  MathSciNet  MATH  Google Scholar 

  35. Ren, B., Cheng, X.P., Lin, J.: The \((2+1)\)-dimensional Konopelchenko–Dubrovsky equation: nonlocal symmetries and interaction solutions. Nonlinear Dyn. 86(3), 1855–1862 (2016)

    Article  MathSciNet  MATH  Google Scholar 

  36. Saha, A., Chatterjee, P.: Dust ion acoustic traveling waves in the framework of a modified Kadomtsev–Petviashvili equation in a magnetized dusty plasma with superthermal electrons. Astrophys. Space Sci. 349(2), 813–820 (2014)

    Article  Google Scholar 

  37. Salas, A.H.: Construction of N-soliton solutions to \((2+1)\)-dimensional Konopelchenko–Dubrovsky (KD) equations. Appl. Math. Comput. 217(18), 7391–7399 (2011)

    MathSciNet  MATH  Google Scholar 

  38. Seadawy, A.R., El-Rashidy, K.: Dispersive solitary wave solutions of Kadomtsev–Petviashvili and modified Kadomtsev–Petviashvili dynamical equations in unmagnetized dust plasma. Results Phys. 8, 1216–1222 (2018)

    Article  Google Scholar 

  39. Shen, S.F., Feng, B.F., Ohta, Y.: From the real and complex coupled dispersionless equations to the real and complex short pulse equations. Stud. Appl. Math. 136(1), 64–88 (2016)

    Article  MathSciNet  MATH  Google Scholar 

  40. Sun, B.N.: General soliton solutions to a nonlocal long-wave–short-wave resonance interaction equation with nonzero boundary condition. Nonlinear Dyn. 92(3), 1369–1377 (2018)

    Article  MATH  Google Scholar 

  41. Sun, B.N., Wazwaz, A.M.: Interaction of lumps and dark solitons in the Mel’nikov equation. Nonlinear Dyn. 92(4), 2049–2059 (2018)

    Article  MATH  Google Scholar 

  42. Veerakumar, V., Daniel, M.: Modified Kadomtsev–Petviashvili (MKP) equation and electromagnetic soliton. Math. Comput. Simul. 62(1–2), 163–169 (2003)

    Article  MathSciNet  MATH  Google Scholar 

  43. Wang, X., Wang, L.: Darboux transformation and nonautonomous solitons for a modified Kadomtsev–Petviashvili equation with variable coefficients. Comput. Math. Appl. 75(12), 4201–4213 (2018)

    Article  MathSciNet  MATH  Google Scholar 

  44. Wu, C.F., Grimshaw, R.H.J., Chow, K.W., Chan, H.N.: A coupled “AB” system: Rogue waves and modulation instabilities. Chaos 25(10), 103113 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  45. Xie, F.D., Yan, Z.Y.: Exactly fractional solutions of the \((2+1)\)-dimensional modified KP equation via some fractional transformations. Chaos Solitons Fractals 36(4), 1108–1112 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  46. Xu, T., Zhang, H.Q., Zhang, Y.X., Li, J., Feng, Q., Tian, B.: Two types of generalized integrable decompositions and new solitary-wave solutions for the modified Kadomtsev–Petviashvili equation with symbolic computation. J. Math. Phys. 49(1), 013501 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  47. Yu, G.F., Xu, Z.W., Hu, J., Zhao, H.Q.: Bright and dark soliton solutions to the AB system and its multi-component generalization. Commun. Nonlinear Sci. Num. Simul. 47, 178–189 (2017)

    Article  MathSciNet  Google Scholar 

  48. Yu, W.F., Lou, S.Y., Yu, J., Yang, D.: Interactions between solitons and cnoidal periodic waves of the \((2+1)\)-dimensional Konopelchenko–Dubrovsky equation. Commun. Theor. Phys. 62(3), 297–300 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  49. Yuan, Y.Q., Tian, B., Liu, L., Wu, X.Y., Sun, Y.: Solitons for the \((2+1)\)-dimensional Konopelchenko–Dubrovsky equations. J. Math. Anal. Appl. 460(1), 476–486 (2018)

    Article  MathSciNet  MATH  Google Scholar 

  50. Zakharov, V.E.: Stability of periodic waves of finite amplitude on the surface of a deep fluid. J. Appl. Mech. Tech. Phys. 9(2), 190–194 (1968)

    Article  Google Scholar 

  51. Zarmi, Y.: Vertex dynamics in multi-soliton solutions of Kadomtsev–Petviashvili II equation. Nonlinearity 27(6), 1499–1523 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  52. Zhao, X.S., Xu, W., Jia, H.B., Zhou, H.X.: Solitary wave solutions for the modified Kadomtsev–Petviashvili equation. Chaos Solitons Fractals 34(2), 465–475 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  53. Zhao, Z.L.: Bäcklund transformations, rational solutions and soliton-cnoidal wave solutions of the modified Kadomtsev–Petviashvili equation. Appl. Math. Lett. 89, 103–110 (2019)

    Article  MathSciNet  MATH  Google Scholar 

  54. Zhao, Z.L., Han, B.: Lie symmetry analysis, Bäcklund transformations, and exact solutions of a \((2 + 1)\)-dimensional Boiti–Leon–Pempinelli system. J. Math. Phys. 58(10), 101514 (2017)

    Article  MathSciNet  MATH  Google Scholar 

Download references

Acknowledgements

This work was supported by the National Natural Science Foundation of China (Grant No. 11701382) and the Natural Science Foundation of Shenzhen University (Grant No. 2019037). We would like to thank Robert Conte and Johan Springael for the helpful discussions.

Author information

Authors and Affiliations

  1. Institute for Advanced Study, Shenzhen University, Shenzhen, 518060, China

    Shuting Huang & Chengfa Wu

  2. College of Mechatronics and Control Engineering, Shenzhen University, Shenzhen, 518060, China

    Cheng Qi

Authors
  1. Shuting Huang
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Chengfa Wu
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Cheng Qi
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Cheng Qi.

Ethics declarations

Conflict of interest

The authors declare that they have no conflict of interest concerning the publication of this manuscript.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Huang, S., Wu, C. & Qi, C. Rational and semi-rational solutions of the modified Kadomtsev–Petviashvili equation and the \(\varvec{(2 + 1)}\)-dimensional Konopelchenko–Dubrovsky equation . Nonlinear Dyn 97, 2829–2841 (2019). https://doi.org/10.1007/s11071-019-05166-4

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11071-019-05166-4

Keywords

Search

Navigation