Nonlinear multi-element interactions in an elastically coupled microcantilever array subject to electrodynamic excitation

Abstract

In this work, we formulate and investigate a nonlinear initial boundary-value problem for an array of N elastically coupled hybrid microcantilever beams that are subject to electrodynamic excitation. The equations of motion for the individual viscoelastic element consist of two fields: the base component which is common to all cantilevers and the unrestrained component which is excited electrodynamically. The coupling of the elements is obtained via an equivalent linear stiffness that is estimated from experimental measurements of a 5-element array. We employ a Galerkin ansatz to obtain a modal dynamical system that consistently incorporates a quintic nonlinearity due to the combined effects of cubic viscoelasticity and quadratic electrodynamics. We validate the periodic response of a 5-element array with moderate damping and construct numerically a comprehensive bifurcation structure for a 25-element array. The analysis reveals an intricate structure for small damping that includes both quasiperiodic and nonstationary chaotic-like energy transfer between the elements of the array. It is noteworthy that an array with a larger coupling stiffness, corresponding to a smaller distance between adjacent elements, yields a chaotic bifurcation structure for a larger value of viscoelastic damping.

Appendices

Appendix A: Nonlinear damping of a single field cantilever

Following [27], the equations of motion for a beam can be written as

$$\begin{aligned}&(F_{1}\cos \varTheta _{3})_{x}-(F_{2}\sin \varTheta _{3})_{x}=m{U}_{tt} \end{aligned}$$

(7.1)

$$\begin{aligned}&(F_{1}\sin \varTheta _{3})_{x}+(F_{2}\cos \varTheta _{3})_{x}=m{W}_{tt} \end{aligned}$$

(7.2)

Neglecting rotary inertia ($j_{3}=0$) the equilibrium of moments with respect to y direction for a beam [27] are given by

$$\begin{aligned} M_{3x}\hbox {d}s+ & {} F_{2}\hbox {d}x(1+e)=0,\,\,\mathrm{{or}}\,\,F_{2}=-\frac{M_{3x}}{1+e} \end{aligned}$$

(7.3)

where $F_{1}$, $F_{2}$ are the resultant stresses, $M_{3}$ is the moment, $\varTheta _{3}$ is the rotational angle, and e is axial strain for the displacements U and W. The axial strain e is defined as a function of the displacements U and W [27] as

$$\begin{aligned} e= & {} \sqrt{(1+U_{x})^2+W_{x}^2}-1 \end{aligned}$$

(7.4)

and the bending curvature $\rho _{3}$ is defined as a function of rotational angle $\varTheta _{3}$ as

$$\begin{aligned} \rho _{3}= & {} \varTheta _{3x} \end{aligned}$$

(7.5)

where the displacements U and W are related to rotational angle $\varTheta _{3}$ as [27]

$$\begin{aligned} \cos \varTheta _{3}=\frac{1+U_{x}}{1+e}\qquad \mathrm{{and}} \qquad \sin \varTheta _{3}=\frac{W_{x}}{1+e} \end{aligned}$$

(7.6)

The viscoelastic constitutive law incorporating a Voigt–Kelvin strain-rate-dependent damping is

$$\begin{aligned} \sigma _{11}=E\epsilon _{11}+D\epsilon _{11t} \end{aligned}$$

(7.7)

where

$$\begin{aligned} \epsilon _{11}= & {} -\frac{\partial U}{\partial x}. i_{1}=e-y\rho _{3} \\ \epsilon _{11t}= & {} \frac{(1+U_{x})U_{xt}+W_{x}W_{xt}}{1+e}-y\rho _{3t}\\ \epsilon _{12}= & {} \epsilon _{22}=\epsilon _{33}=\epsilon _{13}=\epsilon _{23}=0 \end{aligned}$$

Considering isotropic materials for the beam, assuming that the reference line coincides with the centroidal line and using Eq. (7.7), the moment equation can be written as

$$\begin{aligned} M_{3}= & {} -\int _{A}\sigma _{11}y\hbox {d}A=\int _{A}E(-ye+y^2\rho _{3})\hbox {d}A\nonumber \\&+\int _{A}D\Bigg (-\frac{(1+U_{x})U_{xt}+W_{x}W_{xt}}{1+e}y+y^2{\rho }_{3t}\Bigg )\hbox {d}A\nonumber \\ \end{aligned}$$

(7.8)

Assuming that the beam is inextensible ($e=0$) Eq. (7.8) becomes

$$\begin{aligned} M_{3}=EI\rho _{3}+DI{\rho _{3t}} \end{aligned}$$

(7.9)

For inextensible condition of the beam ($e=0$), Eqs. (7.4) and (7.6) are rewritten as

$$\begin{aligned} U_{x}= & {} \sqrt{1-W_{x}^{2}}-1 \end{aligned}$$

(7.10)

$$\begin{aligned} \cos \varTheta _{3}= & {} 1+U_{x}=\sqrt{1-W_{x}^2},\,\mathrm{{and}}\,\sin \varTheta _{3}=W_{x}\nonumber \\ \end{aligned}$$

(7.11)

Integrating Eq. (7.10) once with respect to x and using the boundary conditions $U=0$ at $x=0$, we obtain

$$\begin{aligned} U=\int _{0}^{x}[\sqrt{1-W_{x}^{2}}-1]\hbox {d}x \end{aligned}$$

(7.12)

Integrating Eq. (7.1) once with respect to x and using the boundary condition $F_{x}=0$ at $x=L$, yields

$$\begin{aligned}&F_{1}\cos \varTheta _{3}-F_{2}\sin \varTheta _{3}=\int _{L}^{s}mU_{tt}\hbox {d}s \nonumber \\&\mathrm{{or}} \nonumber \\&F_{1}=\frac{1}{\cos \varTheta _{3}}\Bigg [\int _{L}^{s}mU_{tt}\hbox {d}s+F_{2}\sin \varTheta _{3}\Bigg ] \end{aligned}$$

(7.13)

Differentiating Eq. (7.12) twice with respect to t and interchanging the order of integration and differentiation, we obtain

$$\begin{aligned} U_{tt}=\int _{0}^{x}\frac{\partial ^2}{\partial t^2}\sqrt{1-W_{x}^{2}}\hbox {d}s \end{aligned}$$

Hence,

$$\begin{aligned} \int _{L}^{x}mU_{tt}\hbox {d}x=\int _{L}^{x}m\int _{0}^{x}\frac{\partial ^2}{\partial t^2}\sqrt{1-W_{x}^{2}}\hbox {d}x \hbox {d}x \end{aligned}$$

(7.14)

Substituting Eqs. (7.11) and (7.14) into Eq. (7.13) yields

$$\begin{aligned} F_{1}= & {} \frac{1}{\sqrt{1-W_{x}^{2}}}\Bigg [\int _{L}^{x} m \int _{0}^{x}\frac{\partial ^2}{\partial t^2}\sqrt{1-W_{x}^2}\hbox {d}x \hbox {d}x \nonumber \\&+F_{2}W_{x}\Bigg ] \end{aligned}$$

(7.15)

The bending curvature $\rho _{3}$ and the rotational angle $\varTheta _{3}$ are related using Eqs. (7.5) and (7.11) as

$$\begin{aligned} \rho _{3}=\varTheta _{3x}=(\sin ^{-1}W_{x})_{x} \end{aligned}$$

(7.16)

Substituting Eq. (7.16) into Eq. (7.9) yields

$$\begin{aligned} M_{3}= & {} EI\rho _{3}+DI\rho _{3t}=EI(\sin ^{-1}W_{x})_{x}\nonumber \\&\qquad \qquad \qquad \qquad +DI(\sin ^{-1}W_{x})_{xt} \end{aligned}$$

(7.17)

Substituting $M_{3}$ from Eq. (7.17) into Eq. (7.3) with $e=0$ yields

$$\begin{aligned} F_{2}=-\Big [EI(\sin ^{-1}W_{x})_{x}+DI(\sin ^{-1}W_{x})_{xt}\Big ]_{x} \end{aligned}$$

(7.18)

Substituting Eqs. (7.15) and (7.18) into Eq. (7.2) and using Eq. (7.11), yields equation of motion

$$\begin{aligned}&\Bigg [\frac{W_{x}}{\sqrt{1-W_{x}^2}}\int _{L}^{x}m\int _{0}^{x}\frac{\partial ^2}{\partial t^2}\sqrt{1-W_{x}^2}\hbox {d}x \hbox {d}x\Bigg ]_{x}\nonumber \\&\quad -\Bigg [\frac{[EI(\sin ^{-1}W_{x})_{x}]_{x}}{\sqrt{1-W_{x}^2}}\Bigg ]_{x}{-}\Bigg [\frac{[DI(\sin ^{-1}W_{x})_{xt}]_{x}}{\sqrt{1-W_{x}^2}}\Bigg ]_{x}\nonumber \\&\quad +\,q_{2}=mW_{tt} \end{aligned}$$

(7.19)

Expanding the terms in Eq. (7.19) for small W upto cubic terms yields

$$\begin{aligned}&\rho AW_{tt}+DI\Bigg (W_{xxxt}+W_{xt}W_{xx}^2+W_{xxxt}W_{x}^2\Bigg )_{x}\nonumber \\&\quad +EI\Bigg (W_{xxx}+W_{x}\big ({{W}_{x}}W_{xx}\big )_{x}\Bigg )_{x}\nonumber \\&\quad +\frac{1}{2}\rho A\Bigg [W_{x}\int _{L}^{x}\Bigg (\int _{0}^{x}W_{x}^2\hbox {d}x\Bigg )_{tt}\hbox {d}x\Bigg ]_{x}=Q_{V}\nonumber \\ \end{aligned}$$

(7.20)

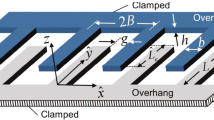
where W, $\rho A$, and EI are the beam transverse displacements, longitudinal mass density, and bending stiffness, respectively. For rectangular cross section, the area is $A=HB$ and the bending moment of inertia is $I=BH^3/12$, where B and H are the beam width and thickness as shown in Fig. 1. D is internal material damping based on a Voigt–Kelvin model [13], respectively. The electrodynamic excitation $Q_{V}$ is given by

$$\begin{aligned} Q_{V}={\frac{\epsilon _{0}B}{2}} {{V}_{f}}^2 \left[ \frac{1}{\big (d-W\big )^2}\right] \end{aligned}$$

(7.21)

where ${V}_{f}=V_\mathrm{dc}+V_\mathrm{ac}\cos (\varOmega t)$, d is distance between beam and bottom substrate $\epsilon _{0}=8.854\times 10^{-12}$ is permitivity of free space. The corresponding boundary conditions of a microbeam are as follows

$$\begin{aligned} W(0,t){=}W_{x}(0,t){=}0,\,\, W_{xx}(L,t){=}W_{xxx}(L,t)=0 \nonumber \\ \end{aligned}$$

(7.22)

We nondimensionalize the governing equations with the variables $w={W}/{d}$, $s={x}/{L}$ and $\tau ={t}/{T_{s}}$ where $T_{s}^2=({\rho AL^4}/{EI})^2$ and $\omega _{s}=1/T_{s}$. The non-dimensionalized equations of motion are given by

$$\begin{aligned}&w_{\tau \tau }{+}w_{ssss}{+}\mu \Big [w_{sss\tau }{+}\delta (w_{s\tau }w_{ss}^2+w_{sss\tau }w_{s}^2)\Big ]_{s}+\nonumber \\&\quad +\,\delta \Big [w_{s}({{w}_{s}}w_{ss})_{s}\Big ]_{s} {+}\delta \frac{1}{2}\Big [w_{s}\int _{1}^{s}\Big ( \int _{\alpha }^{s}{w^{2}_{s}\hbox {d}s}\Big )_{\tau \tau }\hbox {d}s\Big ]_{s}\nonumber \\&\quad =\, \Big [\frac{(\gamma +\eta \cos (\varOmega _\mathrm{ac}\tau )^2}{\big (1-w\big )^2}\Big ]\qquad \qquad \end{aligned}$$

(7.23)

The nondimensionalize boundary conditions are as follows

$$\begin{aligned} w(0,\tau )=w_{s}(0,\tau )=0,\,w_{ss}(1,\tau ){=}w_{sss}(1,\tau )=0\nonumber \\ \end{aligned}$$

(7.24)

The equivalent non-dimensionalized parameters in Eq. (7.23) are

$$\begin{aligned} \mu= & {} \frac{D\omega _{s}}{E}, \,\delta =\Big (\frac{d}{L}\Big )^2, \, \gamma =\sqrt{\frac{6\epsilon _{0}H}{Ed^3}}\Big (\frac{L}{H}\Big )^2V_\mathrm{dc}, \nonumber \\ \eta= & {} \sqrt{\frac{6\epsilon _{0}H}{Ed^3}}\Big (\frac{L}{H}\Big )^2V_\mathrm{ac},\, \varOmega =\frac{\varOmega _\mathrm{ac}}{\omega _{s}}. \end{aligned}$$

(7.25)

We premultiply Eq. (7.23) by denominator term and derive the modal dynamic equations by applying Galerkin’s method. We substitute the assumed solutions as $w(s,\tau ) = q(\tau )\phi (s)$ into Eq. (7.23), and applying Galerkin’s method, we obtain ordinary differential equation which is of the form

$$\begin{aligned}&[(J_{1}-J_{2}q+J_{3}q^2)+\delta (J_{4}q^2-J_{5}q^3+J_{6}q^4)]q_{\tau \tau }\nonumber \\&\qquad +\, \Big [\mu \Big \{(J_{7}- J_{8}q+J_{9}q^2)+\delta (J_{10}q^2-J_{11}q^3+J_{12}q^4)\Big \}\Big ]q_{\tau }\nonumber \\&\qquad +\,\delta (J_{4}q-J_{5}q^2+J_{6}q^3)q^{2}_{\tau }+(J_{7}- J_{8}q+J_{9}q^2) q\nonumber \\&\qquad +\,\delta (J_{10}q^3-J_{11}q^4+J_{12}q^5)\nonumber \\&\qquad -\,J_{13}(\gamma +\eta \cos (\varOmega _\mathrm{ac}\tau ))^2=0\qquad \qquad \end{aligned}$$

(7.26)

where the various integral coefficients in Eq. (7.26) are given in Eq. (7.27).

$$\begin{aligned} J_{1}= & {} \int _{0}^{1}\phi ^2\hbox {d}s,\, J_{2}=2\int _{0}^{1}\phi ^3\hbox {d}s,\, J_{3}=\int _{0}^{1}\phi ^4\hbox {d}s,\nonumber \\ J_{4}= & {} \int _{0}^{1}\phi \Big [\phi _{ss}\int _{1}^{s}\int _{0}^{s}(\phi _{s}^2)\hbox {d}s\hbox {d}s+\phi _{s}\int _{0}^{s}(\phi _{s}^2)\hbox {d}s\Big ]\hbox {d}s,\nonumber \\ J_{5}= & {} \int _{0}^{1}\phi \Big [2\phi \phi _{ss}\int _{1}^{s}\int _{0}^{s}(\phi _{s}^2)\hbox {d}s\hbox {d}s+2\phi \phi _{s}\int _{0}^{s}(\phi _{s}^2)\hbox {d}s\Big ]\hbox {d}s,\nonumber \\ J_{6}= & {} \int _{0}^{1}\phi \Big [\phi ^2\phi _{ss}\int _{1}^{s}\int _{0}^{s}(\phi _{s}^2)\hbox {d}s\hbox {d}s+\phi ^2\phi _{s}\int _{0}^{s}(\phi _{s}^2)\hbox {d}s\Big ]\hbox {d}s,\nonumber \\ J_{7}= & {} \int _{0}^{1}\phi \phi _{ssss}\hbox {d}s,\, J_{8}=2\int _{0}^{1}\phi ^2\phi _{ssss}\hbox {d}s,\,\nonumber \\ J_{9}= & {} \int _{0}^{1}\phi ^3\phi _{ssss}\hbox {d}s,\,\nonumber \\ J_{10}= & {} \int _{0}^{1}\phi \Big [\phi _{ss}^3+4\phi _{s}\phi _{ss}\phi _{sss}+\phi _{s}^2\phi _{ssss}\Big ]\hbox {d}s\nonumber \\ J_{11}= & {} \int _{0}^{1}2\phi ^2\Big [\phi _{ss}^3+4\phi _{s}\phi _{ss}\phi _{sss}+\phi _{s}^2\phi _{ssss}\Big ]\hbox {d}s,\nonumber \\ J_{12}= & {} \int _{0}^{1}\phi ^3\Big [\phi _{ss}^3+4\phi _{s}\phi _{ss}\phi _{sss}+\phi _{s}^2\phi _{ssss}\Big ]\hbox {d}s\nonumber \\ J_{13}= & {} \int _{0}^{1}\phi \hbox {d}s. \end{aligned}$$

(7.27)

Table 4 Nondimensional wave numbers

Table 5 Dimensions and material properties of a beam

Appendix B: IBVP for a two field cantilever

We consider a microcantilever beam with step-like heterogeneity of its width subjected to electrodynamic excitation along out-of-plane direction as shown in Fig. 1a. The two field equations of motion governing the microcantilever beam as found in [15, 27] are thus

$$\begin{aligned}&\rho A_{1}W_{1,t t}+DI_{1}W_{1,xxxxt}+EI_{1}W_{1,xxxx}=0,\nonumber \\&\quad 0<x<L_{1}\qquad \qquad \end{aligned}$$

(7.28)

$$\begin{aligned}&\rho A_{2}W_{2,t t}+DI_{2}\Big [W_{2,xxxt}+W_{2,xt}W_{2,xx}^2\nonumber \\&\qquad +W_{2,xxxt}W_{2,x}^2\Big ]_{x}\nonumber \\&\qquad +EI_{2}\Big [W_{2,xxx} +W_{2,x}({{W}_{2,x}}W_{2,xx})_{x}\Big ]_{x}\nonumber \\&\qquad +\frac{1}{2}\rho A_{n2}\Big [W_{2,x}\int _{L}^{x}\Big ( \int _{L_{1}}^{x}{W^{2}_{2,x}\hbox {d}x}\Big )_{tt}\hbox {d}x\Big ]_{x}\nonumber \\&\quad =Q_{V},\, L_{1}<x<L\qquad \end{aligned}$$

(7.29)

where $W_{i}$, $\rho A_{i}$, and $EI_{i}$ are the beam transverse displacements, longitudinal mass density, and bending stiffness, respectively. For rectangular cross sections, the area is $A_{i}=HB_{i}$ and the bending moment of inertia is $I_{i}=B_{i}H^3/12$, where $B_{i}$ and H are the beam width and thickness as shown in Fig. 1 and D is internal material damping based on a Voigt–Kelvin model [13]. The electrodynamic excitation $Q_{V}$ along out-of-plane direction is given by

$$\begin{aligned} Q_{V}={\frac{\epsilon _{0}B_{2}}{2}} {{V}_{f}}^2 \Big [\frac{1}{\big (d-W_{2}\big )^2}\Big ] \end{aligned}$$

(7.30)

where ${V}_{f}=V_\mathrm{dc}+V_\mathrm{ac}\cos (\varOmega t)$, d is distance between beam and bottom substrate, $\epsilon _{0}=8.854\times 10^{-12}$ is permitivity of free space. The corresponding fixed boundary conditions of the microbeam are as follows

$$\begin{aligned} W_{1}(0,t)= & {} W_{1,x}(0,t)=0,\,W_{2,xx}(L,t)\nonumber \\= & {} W_{2,xxx}(L,t)=0 \end{aligned}$$

(7.31)

The continuity conditions between two fields at $x=L_{1}$ in Fig. 1 are

$$\begin{aligned}&W_{1}(L_{1},t)=W_{2}(L_{1},t),\, EI_{1}W_{1,xx}(L_{1},t)=EI_{2}\nonumber \\&\quad W_{2,xx}(L_{1},t),\,W_{1,x}(L_{1},t)=W_{2,x}(L_{1},t), \nonumber \\&\quad EI_{1}W_{1,xxx}(L_{1},t)=EI_{2}W_{2,xxx}(L_{1},t) \end{aligned}$$

(7.32)

We nondimensionalize the governing equations with the variables $w_{i}={W_{i}}/{d}$, $s={x}/{L}$ and $\tau ={t}/{T_{s}}$ where $T_{s}^2=({\rho A_{1}L^4}/{EI_{1}})^2$ and $\omega _{s}=1/T_{s}$. The non-dimensionalized equations of motion are given by

$$\begin{aligned}&w_{1,\tau \tau }+w_{1,ssss}+\mu w_{1,ssss\tau }=0,\quad 0<s<\alpha \nonumber \\ \end{aligned}$$

(7.33)

$$\begin{aligned}&w_{2,\tau \tau }+w_{2,ssss}+\mu \Big [w_{2,sss\tau }+\delta (w_{2,s\tau }w_{2,ss}^2\nonumber \\&\qquad +w_{2,sss\tau } w_{2,s}^2)\Big ]_{s}+\delta \Big [w_{2,s}({{w}_{2,s}}w_{2,ss})_{s}\Big ]_{s}\nonumber \\&\qquad +\delta \frac{1}{2}\Big [w_{2,s} \int _{1}^{s}\Big ( \int _{\alpha }^{s}{w^{2}_{2,s}\hbox {d}s}\Big )_{\tau \tau }\hbox {d}s\Big ]_{s}\nonumber \\&\qquad = \Big [\frac{(\gamma +\eta \cos (\varOmega _\mathrm{ac}\tau )^2}{\big (1-w_{2}\big )^2}\Big ]\quad \alpha<s<1 \qquad \qquad \end{aligned}$$

(7.34)

The nondimensionalize boundary conditions and continuity conditions are as follows

$$\begin{aligned} w_{1}(0,\tau )= & {} w_{1,s}(0,\tau )=0,\, \nonumber \\ w_{2,ss}(1,\tau )= & {} w_{2,sss}(1,\tau )=0 \nonumber \\ w_{1}(\alpha ,\tau )= & {} w_{2}(\alpha ,\tau ),\, \nonumber \\ w_{1,ss}(\alpha ,\tau )= & {} \beta w_{2,ss}(\alpha ,\tau ),\, w_{1,s}\nonumber \\ (\alpha ,\tau )= & {} w_{2,s}(\alpha ,\tau ), \,\nonumber \\ w_{1,sss}(\alpha ,\tau )= & {} \beta w_{2,sss}(\alpha ,\tau ) \end{aligned}$$

(7.35)

The equivalent non-dimensionalized parameters in Eqs. (7.33)–(7.35) are written as

$$\begin{aligned} \alpha= & {} \frac{L_{1}}{L},\,\beta =\frac{B_{2}}{B_{1}},\,\mu =\frac{D\omega _{s}}{E}, \, \delta =\Big (\frac{d}{L}\Big )^2,\nonumber \\ \gamma= & {} \sqrt{\frac{6\epsilon _{0}H}{Ed^3}}\Big (\frac{L}{H}\Big )^2V_\mathrm{dc},\, \eta =\sqrt{\frac{6\epsilon _{0}H}{Ed^3}}\Big (\frac{L}{H}\Big )^2V_\mathrm{ac},\nonumber \\ \varOmega= & {} \frac{\varOmega _\mathrm{ac}}{\omega _{s}}.\qquad \, \end{aligned}$$

(7.36)

Table 6 Integral coefficients for n identical beams

1.1 Modal dynamical system

We neglect damping and forcing terms from Eqs. (7.33) and (7.34) which yields the two field equations of motion for the unforced and undamped vibrations $w_{i,\tau \tau }+w_{i,ssss}=0$$(i=0 \ldots 2)$. Substituting $w_{i}=q\phi _{i} (i=1 \ldots 2)$ into resulting equations yields the classical Euler–Bernoulli beam dispersion relationship $\omega _{n}^2=z_{n}^4$. Substituting $w_{i}=q\phi _{i}$$(i=1 \ldots 2)$ into Eq. (7.35) yields

$$\begin{aligned} \phi _{1}(0)= & {} \phi _{1,s}(0)=0\qquad \phi _{2,ss}(1)=\phi _{2,sss}(1)=0 \nonumber \\ \phi _{1}(\alpha )= & {} \phi _{2}(\alpha )\qquad \phi _{1,ss}(\alpha )=\beta \phi _{2,ss}(\alpha ) \nonumber \\ \phi _{1,s}(\alpha )= & {} \phi _{2,s}(\alpha ) \qquad \phi _{1,sss}(\alpha )=\beta \phi _{2,sss}(\alpha )\nonumber \\ \end{aligned}$$

(7.37)

To obtain the mode shapes for two field system, we assume mode shapes of the form

$$\begin{aligned} \phi _{1}(s)= & {} A_{1}\cos (z_{n}s)+A_{2}\sin (z_{n}s)+A_{3}\cosh (z_{n}s)\nonumber \\&+A_{4}\sinh (z_{n}s)\nonumber \\ \phi _{2}(s)= & {} B_{1}\cos (z_{n}s)+B_{2}\sin (z_{n}s)+B_{3}\cosh (z_{n}s)\nonumber \\&+B_{4}\sinh (z_{n}s) \end{aligned}$$

(7.38)

where $A_{j}$ and $B_{j}$ are constants to be determined by the boundary and continuity conditions in Eq. (7.37). Substitution of Eq. (7.38) into Eq. (7.37) yields an algebraic linear system of equations, which has a nontrivial solution if the determinant of the following coefficient matrix vanishes.

$$\begin{aligned}&M\nonumber \\&=\left[ \begin{array}{cccccccc} 1&{}0&{}1&{}0&{}0&{}0&{}0&{}0\\ 0 &{}z_{n}&{}0&{}z_{n}&{}0&{}0&{}0&{}0\\ C\alpha &{}S\alpha &{}{ CH}\alpha &{}{ SH}\alpha &{}-C\alpha &{}-S\alpha &{}-{ CH}\alpha &{}-{ SH}\alpha \\ -S\alpha &{}C\alpha &{}{ SH}\alpha &{}{ CH} \alpha &{}S\alpha &{}-C\alpha &{}-{ SH}\alpha &{}-{ CH}\alpha \\ -C\alpha &{}-S\alpha &{}{ CH}\alpha &{}{ SH} \alpha &{}\beta C\alpha &{}\beta S\alpha &{}-\beta { CH}\alpha &{}-\beta { SH}\alpha \\ S\alpha &{}-C\alpha &{}{ SH}\alpha &{} { CH}\alpha &{}-\beta S\alpha &{}\beta C\alpha &{}-\beta { SH}\alpha &{} -\beta { CH}\alpha \\ 0&{}0&{}0&{}0&{}-{ C1}&{}-{ S1} &{}{ CH1}&{}{ SH1}\\ 0&{}0&{}0&{}0&{}{ S1}&{}-{ C1}&{}{ SH1}&{}{ CH1}\end{array} \right] \nonumber \\ \end{aligned}$$

(7.39)

where $C\alpha =\cos (z_{n}\alpha )$, $S\alpha =\sin (z_{n}\alpha )$, $CH\alpha =\cosh (z_{n}\alpha )$, $SH\alpha =\sinh (z_{n}\alpha )$,$C1=\cos (z_{n})$, $S1=\sin (z_{n})$, $CH1=\cosh (z_{n})$, $SH1=\sinh (z_{n})$. We find the determinant of Eq. (7.39) and solve it for $z_{n}$ for different values of $\alpha$ and $\beta$. We substitute back $z_{n}$ into Eq. (7.38), and using Eq. (7.37), we solve the simultaneous equations to find the constants $A_{j}$ and $B_{j}$ which satisfies the orthogonality condition for various values of $\alpha$ and $\beta$. The nondimensional wave numbers for different $\alpha$ and $\beta$ are shown in Table 4.

We premultiply Eqs. (7.33) and (7.34) by denominator in Eq. (7.34) and derive the modal dynamic equations by applying Galerkin’s method. We substitute the assumed solutions as $w_{i}(s, \tau ) = q(\tau )\phi _{i}(s) (i=1 \ldots 2)$ into Eqs. (7.33) and (7.34), and applying Galerkin’s method, we obtain ordinary differential equation which is of the form

$$\begin{aligned}&[(J_{11}{-}J_{12}q{+}J_{13}q^2)+\delta (J_{14}q^2-J_{15}q^3+J_{16}q^4)]q_{\tau \tau }\nonumber \\&\quad + \,\Big [\mu _{1} \Big \{(J_{17}- J_{18}q+J_{19}q^2)+\delta (J_{110}q^2-J_{111}q^3\nonumber \\&\quad +\,J_{112}q^4)\Big \}+\delta (J_{14}q-J_{15}q^2+J_{16}q^3)q^{2}_{\tau }\nonumber \\&\quad +\,(J_{17}- J_{18}q+J_{19}q^2) q\nonumber \\&\quad +\,\delta (J_{110}q^3-J_{111}q^4+J_{112}q^5)-J_{113}(\gamma \nonumber \\&\quad +\,\eta \cos (\varOmega _\mathrm{ac}\tau ))^2=0 \qquad \,\, \end{aligned}$$

(7.40)

where the various integral coefficients in Eq. (7.40) are as follows

$$\begin{aligned} J_{11}= & {} \int _{0}^{\alpha }\phi _{1}^2\hbox {d}s+\int _{\alpha }^{1}\phi _{2}^2\hbox {d}s,\,\nonumber \\ J_{12}= & {} 2\int _{0}^{\alpha }\phi _{1}^2\phi _{2}\hbox {d}s+2\int _{\alpha }^{1}\phi _{2}^3\hbox {d}s,\nonumber \\ J_{13}= & {} \int _{0}^{\alpha }\phi _{1}^2\phi _{2}^2\hbox {d}s+\int _{\alpha }^{1}\phi _{2}^4\hbox {d}s,\nonumber \\ J_{14}= & {} \int _{\alpha }^{1}\phi _{2}\Big [\phi _{2ss}\int _{1}^{s}\int _{\alpha }^{s}(\phi _{2s}^2)\hbox {d}s\hbox {d}s+\phi _{2s}\int _{\alpha }^{s}(\phi _{2s}^2)\hbox {d}s\Big ]\hbox {d}s\nonumber \\ J_{15}= & {} \int _{\alpha }^{1}\phi _{2}\Big [2\phi _{2}\phi _{2ss}\int _{1}^{s}\int _{\alpha }^{s}(\phi _{2s}^2)\hbox {d}s\hbox {d}s\nonumber \\&+2\phi _{2}\phi _{2s}\int _{\alpha }^{s}(\phi _{2s}^2)\hbox {d}s\Big ]\hbox {d}s\nonumber \\ J_{16}= & {} \int _{\alpha }^{1}\phi _{2}\Big [\phi _{2}^2\phi _{2ss}\int _{1}^{s}\int _{\alpha }^{s}(\phi _{2s}^2)\hbox {d}s\hbox {d}s\nonumber \\&+\,\phi _{2}^2\phi _{2s}\int _{\alpha }^{s}(\phi _{2s}^2)\hbox {d}s\Big ]\hbox {d}s\nonumber \\ J_{17}= & {} \int _{0}^{\alpha }\phi _{1}\phi _{1ssss}\hbox {d}s+\int _{\alpha }^{1}\phi _{2}\phi _{2ssss}\hbox {d}s,\nonumber \\ J_{18}= & {} 2\int _{0}^{\alpha }\phi _{1}\phi _{2}\phi _{1ssss}\hbox {d}s+2\int _{\alpha }^{1}\phi _{2}^2\phi _{2ssss}\hbox {d}s\nonumber \\ J_{19}= & {} \int _{0}^{\alpha }\phi _{1}\phi _{2}^2\phi _{1ssss}\hbox {d}s+\int _{\alpha }^{1}\phi _{2}^3\phi _{2ssss}\hbox {d}s,\nonumber \\ J_{110}= & {} \int _{\alpha }^{1}\phi _{2}\Big [\phi _{2ss}^3+4\phi _{2s}\phi _{2ss}\phi _{2sss}+\phi _{2s}^2\phi _{2ssss}\Big ]\hbox {d}s\nonumber \\ J_{111}= & {} \int _{\alpha }^{1}2\phi _{2}^2\Big [\phi _{2ss}^3+4\phi _{2s}\phi _{2ss}\phi _{2sss}+\phi _{2s}^2\phi _{2ssss}\Big ]\hbox {d}s,\nonumber \\ J_{112}= & {} \int _{\alpha }^{1}\phi _{2}^3\Big [\phi _{2ss}^3+4\phi _{2s}\phi _{2ss}\phi _{2sss}+\phi _{2s}^2\phi _{2ssss}\Big ]\hbox {d}s,\nonumber \\ J_{113}= & {} \int _{\alpha }^{1}\phi _{2}\hbox {d}s,\nonumber \\ \end{aligned}$$

(7.41)

Appendix C: Properties of the array

This appendix includes dimensions, material properties, and physical parameters for $\kappa =3.3\times 10^5$ (estimated value) and for $\kappa =1.3\times 10^6$ given in Table 5.

Appendix D: Integral coefficients for the array

This appendix includes integral coefficients of Eq. (2.13). All integral coefficients evaluated for $\alpha =0.075$, $\beta =0.22$ and for $\alpha =0.075$, $\beta =0.12$ are given in Table 6.

$$\begin{aligned} J_{n1}= & {} \int _{0}^{\alpha }\phi _{n1}^2\hbox {d}s+\int _{\alpha }^{1}\phi _{n2}^2\hbox {d}s,\nonumber \\ J_{n2}= & {} 2\int _{0}^{\alpha }\phi _{n1}^2\phi _{n2}\hbox {d}s+2\int _{\alpha }^{1}\phi _{n2}^3\hbox {d}s,\nonumber \\ J_{n3}= & {} \int _{0}^{\alpha }\phi _{n1}^2\phi _{n2}^2\hbox {d}s+\int _{\alpha }^{1}\phi _{n2}^4\hbox {d}s,\nonumber \\ J_{n4}= & {} \int _{\alpha }^{1}\phi _{n2}\Big [\phi _{n2ss}\int _{1}^{s}\int _{\alpha }^{s}2(\phi _{n2s}^2)\hbox {d}s\hbox {d}s\nonumber \\&+\,\phi _{n2s}\int _{\alpha }^{s}2(\phi _{n2s}^2)\hbox {d}s\Big ]\hbox {d}s\nonumber \\ J_{n5}= & {} \int _{\alpha }^{1}\phi _{n2}\Big [2\phi _{n2}\phi _{n2ss}\int _{1}^{s}\int _{\alpha }^{s}2(\phi _{n2s}^2)\hbox {d}s\hbox {d}s\nonumber \\&+\,2\phi _{n2}\phi _{n2s}\int _{\alpha }^{s}2(\phi _{n2s}^2)\hbox {d}s\Big ]\hbox {d}s\nonumber \\ J_{n6}= & {} \int _{\alpha }^{1}\phi _{n2}\Big [\phi _{n2}^2\phi _{n2ss}\int _{1}^{s}\int _{\alpha }^{s}2(\phi _{n2s}^2)\hbox {d}s\hbox {d}s\nonumber \\&+\,\phi _{n2}^2\phi _{n2s}\int _{\alpha }^{s}2(\phi _{n2s}^2)\hbox {d}s\Big ]\hbox {d}s\nonumber \\ J_{n7}= & {} \int _{0}^{\alpha }\phi _{n1}\phi _{n1ssss}\hbox {d}s+\int _{\alpha }^{1}\phi _{n2}\phi _{n2ssss}\hbox {d}s,\nonumber \\ J_{n8}= & {} 2\int _{0}^{\alpha }\phi _{n1}\phi _{n2}\phi _{n1ssss}\hbox {d}s+2\int _{\alpha }^{1}\phi _{n2}^2\phi _{n2ssss}\hbox {d}s \nonumber \\ J_{n9}= & {} \int _{0}^{\alpha }\phi _{n1}\phi _{n2}^2\phi _{n1ssss}\hbox {d}s+\int _{\alpha }^{1}\phi _{n2}^3\phi _{n2ssss}\hbox {d}s,\nonumber \\ J_{n10}= & {} \int _{\alpha }^{1}\phi _{n2}\Big [\phi _{n2ss}^3+4\phi _{n2s}\phi _{n2ss}\phi _{n2sss}+\phi _{n2s}^2\phi _{n2ssss}\Big ]\hbox {d}s\nonumber \\ J_{n11}= & {} \int _{\alpha }^{1}2\phi _{n2}^2\Big [\phi _{n2ss}^3+4\phi _{n2s}\phi _{n2ss}\phi _{n2sss}+\phi _{n2s}^2\phi _{n2ssss}\Big ]\hbox {d}s\nonumber \\ J_{n12}= & {} \int _{\alpha }^{1}\phi _{n2}^3\Big [\phi _{n2ss}^3+4\phi _{n2s}\phi _{n2ss}\phi _{n2sss}+\phi _{n2s}^2\phi _{n2ssss}\Big ]\hbox {d}s\nonumber \\ J_{n13}= & {} \int _{0}^{\alpha }\phi _{n1}^2\hbox {d}s, J_{n14}=2\int _{0}^{\alpha }\phi _{n2}\phi _{n1}^2\hbox {d}s,\nonumber \\ J_{n15}= & {} \int _{0}^{\alpha }\phi _{n2}^2\phi _{n1}^2\hbox {d}s,J_{n16}=\int _{0}^{\alpha }\phi _{n1}\phi _{(n-1)1}\hbox {d}s,\nonumber \\ J_{n17}= & {} 2\int _{0}^{\alpha }\phi _{n2}\phi _{n1}\phi _{(n-1)1}\hbox {d}s,\nonumber \\ J_{n18}= & {} \int _{0}^{\alpha }\phi _{n2}^2\phi _{n1}\phi _{(n-1)1}\hbox {d}s ,\, J_{n19}=\int _{0}^{\alpha }\phi _{n1}\phi _{(n+1)1}\hbox {d}s,\nonumber \\ J_{n20}= & {} 2\int _{0}^{\alpha }\phi _{n2}\phi _{n1}\phi _{(n+1)1}\hbox {d}s \nonumber \\ J_{n21}= & {} \int _{0}^{\alpha }\phi _{n2}^2\phi _{n1}\phi _{(n+1)1}\hbox {d}s, \, J_{n22}=\int _{\alpha }^{1}\phi _{n2}\hbox {d}s, \end{aligned}$$

(7.42)

Note that for identical beams $J_{nj}$ are equal and $\phi _{n-1}=\phi _{n}=\phi _{n+1}$ for all n.