Nonlinear oscillations of a pendulum cable with the effects of the friction and the radius of the support

Abstract

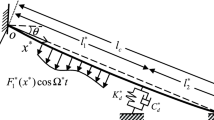
The dynamics of a pendulum cable with a special constitutive law subjected to a time-dependent velocity is investigated. The Coulomb friction between the cable of pendulum and its support taking into account the effects of the support is considered. To predict system behaviors, the multiple scales method is endowed leading to spot the evolution of the angle and the length of the pendulum. The study permits to enlighten the effects of velocity, friction and the radius of the wheel support on the overall system response and its stability.

Appendices

Appendices

Expression of functions

$$\begin{aligned} \varTheta _{1,1}= & {} \theta _0 \nonumber \\ \varTheta _{1,2}= & {} 0\nonumber \\ \varTheta _{2,1}= & {} 0\nonumber \\ \varTheta _{2,2}= & {} -\frac{7 v_0 \theta _0}{8 \omega _0l_0}\nonumber \\ \varTheta _{3,1}= & {} \frac{1}{192} \theta _0 \nonumber \\&\times \left( \frac{45 v_0^2}{l_0^2 \omega _0^2}\right. \left. -\frac{\theta _0^2 \left( 2880 \omega _0^6-1012 \omega _0^4+137 \omega _0^2+11\right) }{\left( 1-4 \omega _0^2\right) ^2}\right) \nonumber \\&+\,\mu \frac{\theta _0^2 \left( 10 \omega _0^2-3\right) }{2 l_0 \left( 4 \omega _0^2-1\right) }T^* +\frac{\theta _0^2 \left( 22 \omega _0^2-7\right) }{6 l_0 \left( 4 \omega _0^2-1\right) } R^*\nonumber \\ \varTheta _{3,2}= & {} 0 \end{aligned}$$

(34)

$$\begin{aligned} \xi _{2,1}= & {} -\frac{3 \omega _0^4 \theta _0^2 l_0}{4\omega _0^2-1}+ \mu \frac{\omega _0^2\theta _0 }{ \omega _0^2-1}T^* +\frac{\omega _0^2 \theta _0}{\omega _0^2 - 1}R^* \nonumber \\ \xi _{2,2}= & {} 0 \nonumber \\ \xi _{2,3}= & {} \frac{3 \theta _0^2 l_0 \omega _0^2 \left( 16 \omega _0^2-2 \omega _0-7\right) }{64 \omega _0^2-16} -R\theta _0 -\mu \theta _0 T^*\nonumber \\ \xi _{3,1}= & {} \mu ^2 \frac{\theta _0^2 \omega _0^2}{1-4 \omega _0^2} T^* \nonumber \\ \xi _{3,2}= & {} -\frac{3 \theta _0^2 v_0 \omega _0^4 \left( 12 \omega _0^2-23\right) }{8 \left( 1-4 \omega _0^2\right) ^2} \nonumber \\&\quad -\, \mu \frac{\theta _0 v_0 \omega _0^2 \left( \omega _0^2+7\right) }{8 l_0 \left( \omega _0^2-1\right) ^2}T^*\nonumber \\&\quad \ -\,\frac{\theta _0 v_0 \omega _0^2 \left( \omega _0^2+23\right) }{8 l_0 \left( \omega _0^2-1\right) ^2}R^*\nonumber \\ \xi _{3,3}= & {} \mu ^2\frac{ \theta _0^2 }{4 }T^* \end{aligned}$$

(35)

$$\begin{aligned} c_1(t_{0})= & {} \frac{\theta _0^2 \left( \left( -9 \omega _0^4 \cos (t_{0})+5 \omega _0^4-7 \omega _0^2+2\right) \cos (\omega _0t_{0} )\right) }{3 l_0 (\omega _0-1) (\omega _0+1) \left( 4 \omega _0^2-1\right) } \nonumber \\&\quad +\,\frac{\theta _0^2 \left( \left( 2 \omega _0^2+1\right) \cos (2 \omega _0t_{0} )+3\right) }{6 l_0 (\omega _0-1) (\omega _0+1)} \nonumber \\&\quad +\, \frac{\theta _0^2 \left( 6 \left( \omega _0^2-1\right) \omega _0^3 \sin (t_{0}) \sin (\omega _0t_{0} )\right) }{3 l_0 (\omega _0-1) (\omega _0+1) \left( 4 \omega _0^2-1\right) } \end{aligned}$$

(36)

$$\begin{aligned} c_2(t_{0})= & {} \frac{\theta _0 \sin (\omega _0t_{0})}{32 \omega _0\left( 4 \omega _0^2-1\right) l_0^2} \left( 2 \theta _0^2 \omega _0^2 \left( 24 \omega _0^4-11 \omega _0^2-1\right) l_0^2\right. \nonumber \\&\quad \left. +\,\left( 15-60 \omega _0^2\right) v_0^2\right) \nonumber \\&\quad -\,(\mu T^*+R^*)\frac{\theta _0^2 \omega _0\sin (\omega _0t_{0} )}{2 l_0} \end{aligned}$$

(37)

$$\begin{aligned} c_3(t_{0})= & {} \frac{1}{8} \theta _0 v_0 \omega _0\left[ \frac{2 (R^*+\mu T^*) (\sin (\omega _0t_{0} ) -\omega _0\sin (t_{0}))}{l_0}\right. \nonumber \\&\left. \times (\omega _0^2-1)\right. \nonumber \\&\left. \qquad -\,\frac{3 \theta _0 \omega _0^2 (\sin (2 \omega _0t_{0} )-2 \omega _0\sin (t_{0}))}{4 \omega _0^2-1} \right] \end{aligned}$$

(38)