On the dynamics of a vibration isolator with geometrically nonlinear inerter

Abstract

The inerter is a two-terminal mechanical element that produces forces directly proportional to the relative acceleration between these terminals. The linear behaviour of this element has already been described in the literature. In this work, the nonlinear effects of the geometrical arrangement of the inerter are investigated in terms of vibration isolation and compared to the traditional arrangement. The analysis comprises the use of harmonic-balanced method applied to the exact equation, as well as approximations for low amplitude and high amplitude. Numerical analysis is used to complement the investigation. Comparison with classic vibration isolators shows possible benefits for high frequency regimes. The effects from the geometrical nonlinearity vanish when the amplitude of motion is large.

Appendices

Polynomial terms

The polynomial terms defining Eqs. 24 and 25:

$$\begin{aligned} P_1= & {} -\frac{5}{8}\left( \left( \mu + 1\right) \varOmega ^2 - 1\right) H^5 \nonumber \\&- \,\frac{1}{2} \left( \left( 1 \mu +3\right) \varOmega ^2-3\right) H^3\nonumber \\&+ \,\left( 1- \varOmega ^2 \right) H \end{aligned}$$

(38)

$$\begin{aligned} P_2= & {} -\frac{1}{4}\left( \xi \varOmega H^5 + 4 \xi \varOmega H^3 + 8 \xi \varOmega H \right) \end{aligned}$$

(39)

$$\begin{aligned} P_3= & {} -\frac{1}{4}\left( \varOmega ^2 H^4 + 2\varOmega ^2 H^2 \right) \hat{X}_0 \end{aligned}$$

(40)

Polynomial terms: stability

The polynomial terms defining the stability Eqs. 33 and 34:

$$\begin{aligned} T8= & {} \frac{125}{64}\left( \mu ^2 + 2\mu + 1\right) \varOmega ^4 \nonumber \\&+ \,\frac{1}{32}\left( 10\xi ^2 -125\mu - 125\right) \varOmega ^2 + \frac{125}{64} \end{aligned}$$

(41)

$$\begin{aligned} T_6= & {} \frac{1}{2}\left( 5\mu ^ 2 + 20 \mu + 15\right) \varOmega ^4 \nonumber \\&+\, \left( 2\xi ^2 - 10 \mu - 15\right) \varOmega ^2 + \frac{15}{2} \end{aligned}$$

(42)

$$\begin{aligned} T_4= & {} \frac{1}{4}\left( 3\mu ^2 + 33\mu + 43\right) \varOmega ^4 \nonumber \\&+\, \frac{1}{4} \left( 24\xi ^2 -33\mu - 84 \right) \varOmega ^2 + 1 \end{aligned}$$

(43)

$$\begin{aligned} T_2= & {} \left( 2\mu + 6\right) \varOmega ^4 + \left( 8\xi ^2 -2\mu - 12\right) \varOmega ^2 + 6 \end{aligned}$$

(44)

$$\begin{aligned} T_0= & {} \varOmega ^4 + \left( 4\xi ^2 -2\right) \varOmega ^2 + 1 \end{aligned}$$

(45)

$$\begin{aligned} W_4= & {} \frac{1}{64} \left( 125\mu ^2+250\mu +125\right) U^8\nonumber \\&+ \,\left( \frac{5}{2}\mu ^2+10\mu +\frac{15}{2}\right) U^{6} \nonumber \\&+\,\frac{1}{64}\left( 48\mu ^2+528\mu +672\right) U^4 \nonumber \\&+\, \left( 2\mu +6\right) U^2 + 1 \end{aligned}$$

(46)

$$\begin{aligned} W_2= & {} \frac{1}{32} \left( 10{\xi }^2-125\mu -125\right) U^8 \nonumber \\&+\,\left( 2{\xi }^2-10\mu -15\right) U^6 \nonumber \\&+\,\frac{1}{4}\left( 24{\xi }^2-33\mu -84\right) U^4 \nonumber \\&+ \,\left( 8 \xi ^2-2\mu -12\right) U^2 + 4 \xi ^2 - 1 \end{aligned}$$

(47)

$$\begin{aligned} W_0= & {} \frac{125}{64} U^8 + \frac{15}{2}U^{6} + \frac{21}{2} U^4 + 6 U^2+1 \end{aligned}$$

(48)

Fig. 23

Comparison of the absolute transmissibility considering the exact equation, the mass–spring–damper, the mass–spring–damper–inerter isolators and a system with an auxiliary TMD. $X_0=0.3$, $\mu =0.3$, $\xi =0.01$

Absolute transmissibility of linear systems

The absolute transmissibility of a linear spring–mass–damper system is given by

$$\begin{aligned} T = \frac{1+j2\xi \varOmega }{1-\varOmega ^2 + j2\xi \varOmega } \end{aligned}$$

(49)

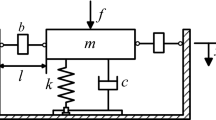
The absolute transmissibility of a linear spring–mass–damper–inerter system of Fig. 2 is given by

$$\begin{aligned} T = \frac{1 -\mu \varOmega ^2 + j2\xi \varOmega }{1-(1+\mu )\varOmega ^2 + j2\xi \varOmega } \end{aligned}$$

(50)

Comparison with tuned mass damper (TMD)

To complement the analysis described in this paper, a comparison of the proposed system with the tuned mass damper is shown in Fig. 23. In this analysis, the natural frequency of the auxiliary system was tuned in the same resonance frequency of the primary system.