Research of giant magnetostrictive actuator’s nonlinear dynamic behaviours

Abstract

The multi-coupled nonlinear factors existing in the giant magnetostrictive actuator (GMA) have a serious impact on its output characteristics. If the structural parameters are not properly designed, it is easy to fall into the nonlinear instability, which has seriously hindered its application in many important fields. The electric–magnetic-machine coupled dynamic mathematical model for GMA is established according to J-A dynamic hysteresis model, ampere circuit law, nonlinear quadratic domain model and structure dynamics equation. Nonlinear dynamic analysis method is applied to study the nonlinear dynamic behaviour of the key structure parameters to reveal their influence on the system stability. The design principle of structural parameters is obtained by studying stability of GMA, which provides theoretical basis and technical support for the structural stability design.

1 Introduction

Since the 1970s, giant magnetostrictive material (GMM) has developed very rapidly as a kind of strategic functional material. It has been widely applied in active vibration isolation, precision control, transducer and many other fields because of its high energy conversion efficiency, large output displacement and good dynamic characteristics [1,2,3]. But, it is very easy to fall into the nonlinear instability in high frequency because of strong multiple nonlinear factors [4,5,6]. The existence of nonlinear instability and even chaotic phenomena in GMA makes it difficult to predict and control, which seriously hinders its application in many important fields. James, Lei Wang, William S and Mao Jianqin applied robust control [7], self-adaptive control algorithm [8], optimal control [9] and $\hbox {H}\infty$ control [10] to reduce the influence of nonlinear factors and improve the tracking accuracy and stability of GMA. The research of GMA structural design is mainly about reducing magnetic flux leakage and improving the magnetic field [11, 12]. So far, researches about how to improve the stability of GMA are mainly done in the control strategies, while there are no deep studies on the reason of nonlinear instability and the structural stability design severely lacks theoretical guidance. Therefore, this paper firstly establishes the electric–magnetic–machine coupled model and then applies bifurcation diagram, Poincaré map, time-domain waveform, phase diagram and spectral analysis to analyse the GMA nonlinear dynamics behaviour characteristics. Finally, the design principles of structural parameters based on stability are achieved and proved in experiment.

Fig. 1

Equivalent model of GMA

2 GMA model

GMA can be seen as a second-order quality-elastic-damping system with one degree of freedom according to its working principle. The equivalent mechanical model is shown in Fig. 1, and the dynamic equation is established according to Newton’s second law.

$$\begin{aligned}&F=-\,\sigma S=M_e \ddot{x}+C_e \dot{x}+F_\mathrm{z} \end{aligned}$$

(1)

$$\begin{aligned}&M_\mathrm{e} =\frac{M_M }{3}+M_L \end{aligned}$$

(2)

where F is the output force of GMM rod, $M_{e}$ is the equivalent mass, $C_{e}$ is the equivalent damping coefficient, $F_{z}$ is the restoring force of disc spring, whose computing method is in appendix A, S is the GMM rod’s cross-sectional area, x is the output displacement of GMA, $M_{M}$ is the mass of GMM rod, $M_{L }$ is mass of the load.

$$\begin{aligned} x=\varepsilon L \end{aligned}$$

(3)

where $\varepsilon$ is the strain of GMM rod, and L is the length of GMM rod.

The quadratic moment domain rotation model is introduced into the linear piezomagnetic equation, and the nonlinear piezomagnetic equation is achieved [13].

$$\begin{aligned} \varepsilon =\sigma /E+\gamma _1 M^{2} \end{aligned}$$

(4)

where $\gamma _1$ is GMM rod’s nonlinear magnetic elasticity coefficient, E is GMM’s elasticity modulus, M is the magnetization intensity, which can be achieved by magnetic field intensity H. The relationship between H and M is described in appendix A.

According to the ampere circuit theorem considering the magnetic flux leakage, when the bias magnetic field is $H_{\mathrm{bias}}$, the magnetic field strength H is

$$\begin{aligned} H=H_{\mathrm{bias}} +k_{\mathrm{coil}} I \end{aligned}$$

(5)

where $k_{\mathrm{coil}}$ is the exciting coefficient.

The nonlinear dynamic model of GMA can be achieved by uniting Eqs. 1–5, which takes the current I as input and displacement x as output.

$$\begin{aligned} M_e \ddot{x}+C_e \dot{x}+K_{e3} x^{3}-K_{e2} x^{2}+K_{e1} x=F(I) \end{aligned}$$

(6)

where $K_{e3} =K_{\mathrm{spr}3}$, $K_{e2} =K_{\mathrm{spr}2}$, $K_{e1} =K_{\mathrm{spr}1} +\frac{ES}{L}$ are the equivalent stiffness coefficients, $F(I)=\gamma _1 ESM(I)^{2}$ is output force produced by GMM rod, M(I) is the magnetization when input current is I.

3 Research of nonlinear dynamic behaviour in GMA

In order to study the dynamic behaviour of GMA, the dynamic equation firstly is normalized and then solved by Runge–Kutta. Qualitative analysis of nonlinear dynamics is applied to study GMA’s nonlinear dynamic behaviour characteristics and reveal the influence of key structural parameters on the system stability.

Fig. 2

Bifurcation diagram of $\varphi _1$

Fig. 3

Response characteristics in $\varphi _1 =10^{-4}$. a Spectrum, b poincaré mapping, c phase diagram, d time-domain waveform

When the dimensionless displacement $u=x/\gamma _0$ and time $\tau =\omega _0 t$ are introduced, Eq. 6 is converted to be Eq. 7, where $\gamma _0 =\sqrt{K_{e1} /K_{e3} }$, $\omega _0 =\sqrt{K_{e1} /M_e }$.

$$\begin{aligned} \ddot{u}+\varphi _1 \dot{u}+u^{3}-\varphi _2 u^{2}+u=f_\varphi F(\Omega \tau ) \end{aligned}$$

(7)

where $\varphi _1 =C_e /\sqrt{M_e K_{e1} }$ is dimensionless damping coefficient, $\varphi _2 =K_{e2} /\sqrt{K_{e1} K_{e3} }$ is square stiffness coefficient, $f_\varphi =\sqrt{K_{e3} /K_{_{e1} }^3 }$ is coupling stiffness coefficient, and $\Omega =\omega /\omega _0$ is angular frequency.

The effects of sensitive parameters on the system stability are revealed by studying the dynamics characteristics for $\varphi _1$, $\varphi _2$ and $f_\varphi$, which provide the theoretical foundation for GMA structure design based on stability.

3.1 Research on the damping coefficient

Taking the dimensionless damping coefficient $\varphi _1$ as the reference variable, the bifurcation diagram is shown in Fig. 2 when $\Omega =3$. The response characteristics are shown in Fig. 3 when $\varphi _1 =10^{-4}$. Spectrum contains multi-frequency, Poincaré mapping is the distribution of random points in the global scope, phase diagram is composed of many circular curves without overlapping, and time-domain waveform is messy without periodicity, which indicates that system is in chaotic state. Figure 4 shows the response characteristics when $\varphi _1 =0.15$. Spectrum shows that the main frequency is the integer times of 1/2 $\Omega$ and Poincaré mapping only has two points, which indicates that the system goes into period-doubling bifurcation. Figure 5 shows that the system is in the stable periodic motion when $\varphi _1 =0.25$.

With the decrease of damping coefficient, system transforms from stable periodic motion, period-doubling bifurcation to chaos, which shows that smaller $\varphi _1$ can fall into the unstable chaotic state.

Fig. 4

Response characteristics in $\varphi _1 =0.15$. a Spectrum, b poincaré mapping

Fig. 5

Time-domain waveform in $\varphi _1 =0.25$

Fig. 6

Bifurcation diagram of $\varphi _2$. a $\Omega =2$, b $\Omega =3$

3.2 Research on the square stiffness coefficient

Taking the dimensionless square stiffness coefficient $\varphi _2$ as the variable, the nonlinear dynamic behaviour characteristics of the GMA are studied when $\Omega =2$ and $\Omega =3$. It can be seen from Fig. 6 that the system maintains the same bifurcation characteristic when $\varphi _2$ varies from 0 to 1 under different $\Omega$. Therefore, $\varphi _2$ has nothing to do with the dynamic behaviour in the GMA.

3.3 Research on the coupling stiffness coefficient

Taking the coupling stiffness coefficient $f_\varphi$ as the variable, the bifurcation diagram is shown in Fig. 7. With the increase of $f_\varphi$, the system goes from stable period, period-doubling bifurcation to chaos, which indicates that the larger $f_\varphi$ makes the system enter the unstable chaotic state.

Fig. 7

Bifurcation diagram of $f_\varphi$

Fig. 8

GMA test bed

Fig. 9

Control system

4 Parameters design based on the stability

It is concluded from Sect. 3 that the larger $\varphi _1$ and smaller $f_\varphi$ can improve the stability according to nonlinear dynamic behaviour characteristics of GMA. According to $\varphi _1 =C_e /\sqrt{M_e K_{e1} }$, larger $C_e$ and smaller $K_{e1}$ can increase $\varphi _1$. But, smaller $K_{e1}$ leads to smaller natural frequency $\omega _0 =\sqrt{K_{e1} /M_e }$. According to $f_\varphi =\sqrt{K_{e3} /K_{_{e1} }^3 }$, increasing $K_{e1}$ and decreasing $K_{e3}$ can decrease $f_\varphi$.Therefore, increasing $C_e$, $K_{e1}$ and decreasing $K_{e3}$ can improve the system stability.

According to $K_{e3} =K_{\mathrm{spr}3}$, $K_{e1} =K_{\mathrm{spr}1} +\frac{ES}{L}$ and disc spring characteristics in appendix A, the following conclusions can be drawn.

• 1. Increasing the GMM rod’s S / L will increase $K_{e1}$ and enhance the stability. So, slender GMM rod is not favourable for stability.

• 2. The coupling stiffness coefficient $f_\varphi$ of A, B, C disc springs increases successively in the same diameter, and A disc spring has higher stability.

• 3. Increasing the diameter D of disc spring can increase $K_{e1}$ and decrease $K_{e3}$, which can enhance the system stability.

• 4. The larger number of disc springs in overlap can reduce $f_\varphi$ and improve stability, while the result of involution is just the opposite.

Fig. 10

Simulation and experiment. a Different frequency, b different loads, c different combination methods of disc springs, d different series of disc springs, e different minor loops

5 Test verification

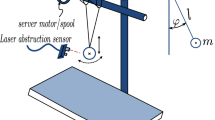
GMA test bed (Fig. 8) is applied to do verification experiment for the mathematical model and stability. It is mainly composed of GMA, laser displacement sensor, temperature control system and control system. V100-MS laser displacement sensor can test the displacement of GMA, and its frequency response is up to 20 kHz. Temperature control system is applied to maintain a stable operating temperature for GMM rod. The diagram of control system is shown in Fig. 9. LabWindows and RTX are used for upper and lower computer, respectively, and sampling period is 0.5 ms. The control card in the industrial personal computer (IPC) sends the introductions to the servo drivers and then generates exciting current to activate GMA. The data acquisition card (DAQ) is used to achieve displacement through laser displacement. When doing some experiments, some experimental conditions must be satisfied.

• 1. The quiet working environment must be ensured, and any outside noise may affect the results.

• 2. The laser beam should be perpendicular to the cross section of output shaft in GMA. Otherwise, it will affect the measurement result.

• 3. Temperature control system should keep working in the experiment to maintain constant working temperature for GMM rod.

1. Mathematical model verification

Figure 10 is the simulation and experiment curve of GMA in different frequency, loads, combination methods, series of disc springs and minor loop. The good fitting proves the correctness and validity of the GMA model.

2. Stability verification

Figure 11 shows the spectrum of GMA output displacement in different structural parameters. When C disc springs are in involution and driving frequency is 166.7 HZ, the output displacement contains a variety of frequency, which indicates that the system is in chaos (Fig. 11a), while the system is in stable periodic motion when C disc springs are in overlap (Fig. 11b). When C disc springs are in overlap and driving frequency is 200 HZ, the system is in chaos (Fig. 11c), while the system is in stable periodic motion when it chooses A disc springs (Fig. 11d). Therefore, the higher structural stiffness can improve the stability of GMA.

Fig. 11

Spectrum in different structural parameters. a Involution of C disc spring in 166.7 HZ, b overlap of C disc spring in 166.7 HZ, c overlap of C disc spring in 200 HZ, d overlap of A disc spring in 200 HZ

6 Conclusion

• 1. Adding structural factors to the GMA mathematical model can effectively improve the accuracy of the model.

• 2. It is possible to cause the system to fall into instability with lower structure rigidity and damping.

• 3. Disc spring plays an important role in stability for GMA. The larger diameter D, higher number of $n_{\mathrm{c}}$ in overlap and A disc spring can effectively improve the stability

Appendix A

1. Working principles of GMA

The working principle of GMA is shown in Fig. 12. The GMM rod drives load under the action of the magnetic field generated by the excitation coil and permanent magnet. GMM needs pre-pressure produced by compacting disc spring to improve the magnetostriction coefficient. The ring permanent magnet can produce bias magnetic field to eliminate the double-frequency property of materials and export bidirectional displacement. Top and lower cover forms closed magnetic circuit to reduce magnetic leakage.

Fig. 12

GMA

2. GMM mode between ${\varvec{H}}$ and ${\varvec{M}}$

Jiles–Atherton (J–A) model is established based on the magnetic wall motion theory existing in ferromagnetic material proposed by Jiles DC and Atherton DL and has developed into a relatively mature theory [14,15,16,17,18]. Classical J–A dynamic H–M model can be given as

$$\begin{aligned}&H_e =H+\alpha M+\frac{9\lambda _s \sigma }{2\mu _0 M_\mathrm{s}^2 }M\nonumber \\&\quad \quad =H+\widetilde{\alpha }M \end{aligned}$$

(A1)

$$\begin{aligned}&M_{\mathrm{an}} =M_\mathrm{s} \left( \coth \frac{H_e }{a}-\frac{a}{H_e }\right) \end{aligned}$$

(A2)

$$\begin{aligned}&M=M_{\mathrm{rev}} +M_{\mathrm{irr}} \end{aligned}$$

(A3)

$$\begin{aligned}&M_{\mathrm{rev}} =c(M_{\mathrm{an}} -M_{\mathrm{irr}} ) \end{aligned}$$

(A4)

$$\begin{aligned}&M_{\mathrm{irr}} =(M-cM_{\mathrm{an}} )/(1-c) \end{aligned}$$

(A5)

$$\begin{aligned}&M=M_{\mathrm{an}} -k\delta (1-c)\frac{\hbox {d}M_{\mathrm{irr}} }{\hbox {d}H_e }-k_1 \frac{\hbox {d}M}{\hbox {dt}}\frac{\hbox {d}M}{\hbox {d}H_e }\nonumber \\&\quad \quad \quad -\,k_2 \left| {\frac{\hbox {d}M}{\hbox {dt}}} \right| ^{\frac{1}{2}}\frac{\hbox {d}M}{\hbox {d}H_e } \end{aligned}$$

(A6)

where $H_e$ is the effective magnetic field intensity, H is the magnetic field intensity, M is the magnetization intensity, $_{ }\alpha$ is the average internal coupling field coefficient, $_{ }\sigma$ is the stress on the GMM rod, $\mu _0$ is the vacuum permeability, $M_\mathrm{s}$ is the saturation magnetization, $\lambda _s$ is the saturation magnetostrictive coefficient, $M_{\mathrm{an}}$ is the anhysteretic magnetization, a is the shape parameter of anhysteretic magnetization, $M_{\mathrm{rev}}$ is the reversible magnetization, $M_{\mathrm{irr}}$ is the irreversible magnetization, c is the reversible loss coefficient, $\delta$ is the direction factor, when $\hbox {d}H/\hbox {dt\,>\,0}$, $\delta =1$ and when $\hbox {d}H/\hbox {dt\,<\,0}$, $\delta =-\,1$, k is irreversible loss coefficient, $k_1$ is the eddy-current loss factor, and $k_2$ is anomalous loss factor.

The minor loop model can be got by modifying parameter $a,\alpha , c$ and k according to the parameters characteristics and the difference between simulation and experiment curves [19].

$$\begin{aligned} \left\{ {\begin{array}{ll} a_{\min or} =ae^{\gamma _a (\lambda _s -\lambda _\mathrm{m} )} \\ \alpha _{\min or} =\alpha e^{\gamma _\alpha (\lambda _s -\lambda _\mathrm{m} )} \\ c_{\min or} =ce^{\gamma _c (\lambda _s -\lambda _\mathrm{m} )} \\ k_{\min or} =ke^{\gamma _k (\lambda _s -\lambda _\mathrm{m} )} \\ \end{array}} \right. \end{aligned}$$

(A7)

where $\gamma _k$, $\gamma _a$, $\gamma _c$ and $\gamma _\alpha$ are the local correction coefficients of k, a, c and $\alpha$, respectively, $k_{\min or}$, $a_{\min or}$, $c_{\min or}$, $\alpha _{\min or}$ are the revised parameters of minor loop, and $\lambda _\mathrm{m}$ is the maximum magnetostrictive coefficient of minor loop.

3. Disc spring model

As the main device to exert pre-pressure on GMA, disc spring has an important influence on the output characteristics of GMA. The restoring force generated by the single disc spring is

$$\begin{aligned} F_d =K_{\mathrm{spr3}} x_f^3 -K_{\mathrm{spr2}} x_f^2 +K_{\mathrm{spr1}} x_f \end{aligned}$$

(A8)

where $K_{\mathrm{spr3}} =\frac{t}{2\chi D^{2}}$, $K_{\mathrm{spr2}} =\frac{3th_0 }{2\chi D^{2}}$, $K_{\mathrm{spr1}} =\frac{h_0^2 t+t^{3}}{\chi D^{2}}$, $x_f$ is the disc spring deformation, and $h_{0}$ is the maximum deformation of disc spring . The structure of the disc spring is shown in Fig. 13.

Fig. 13

Structure of disc spring

According to literature 20, there are A, B and C series of disc springs and the relationship between D, t and $h_0$ is shown Table 1.

Table 1 Relationship between structure parameters of disc spring

Fig. 14

Combination methods of disc springs. a Involution, b overlap, c mixture

It can been seen from Table 1 that no matter what kind of disc spring it is, D / t and $D/h_0$ are constants. So, $K_{\mathrm{spr3}}$, $K_{\mathrm{spr2}}$, $K_{\mathrm{spr1}}$ are converted to Eq. A9.

$$\begin{aligned} \left\{ {\begin{array}{ll} K_{\mathrm{spr1}} =\frac{D}{\chi }\left( \frac{1}{C_t C_{h_0 }^2 }+\frac{1}{C_{_t }^3 }\right) \\ K_{\mathrm{spr2}} =\frac{3}{2\chi C_t C_{h_0 } } \\ K_{\mathrm{spr3}} =\frac{1}{2\chi C_t D} \\ \end{array}} \right. \end{aligned}$$

(A9)

where $D/t=C_t$, $D/h_0 =C_{h_0 }$.

The disc spring also can change its structure stiffness by different combination methods (Fig. 14). Without considering the friction force between the disc springs, the calculation formula for the restoring force $F_{z}$ and total deformation x of the disc spring is shown in Table 2, where $n_{s}$ and $n_{c}$ are the number of disc springs in involution and overlap combination.

Table 2 Characteristics in different combinations

4. parameters

The model parameters for GMA are shown in Table 3 based on physical property and parameters identification [21].

Table 3 Model parameters