Skip to main content
SpringerLink
Log in

Lumps and rogue waves of generalized Nizhnik–Novikov–Veselov equation

  • Original Paper
  • Published:
Nonlinear Dynamics Aims and scope Submit manuscript

Abstract

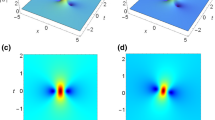
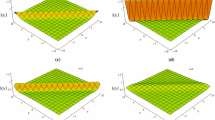
We investigate the generalized \((2+1)\) Nizhnik–Novikov–Veselov equation and construct its linear eigenvalue problem in the coordinate space from the results of singularity structure analysis thereby dispelling the notion of weak Lax pair. We then exploit the Lax pair employing Darboux transformation and generate lumps and rogue waves. The dynamics of lumps and rogue waves is then investigated.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5

Similar content being viewed by others

References

  1. Boiti, M., Leon, J.P., Martina, L., Pempinelli, F.: Scattering of localized solitons in the plane. Phys. Lett. A 132, 432–439 (1988)

    Article  MathSciNet  Google Scholar 

  2. Fokas, A.S., Santini, P.M.: Dromions and a boundary value problem for the Davey–Stewartsan I equation. Physica D 44, 99–130 (1990)

    Article  MATH  MathSciNet  Google Scholar 

  3. Chen, J., Feng, B.F., Chen, Y.: General brightdark soliton solution to (2 \(+\) 1)-dimensional multi-component long-wave–short-wave resonance interaction system. Nonlinear Dyn. 88, 1273–1288 (2017)

    Article  Google Scholar 

  4. Estevez, P.G., Prada, J., Villarroel, J.: On an algorithmic construction of lump solution in a \((2+1)\) integrable equation. J. Phys. A Math. Theor. 40, 7213–7231 (2007)

    Article  MATH  MathSciNet  Google Scholar 

  5. Liming, L., Bao, F., Zuonong, Z.: Multisoliton, multibreather, and higher order rogue wave solution to the complex short pulse equation. Physica D 327, 13–29 (2016)

    Article  MATH  MathSciNet  Google Scholar 

  6. Chang, L., Zeping, W.: Rogue waves in the \((2+1)\) dimensional nonlinear Schrödinger equations. Int. J. Numer. Meth. Heat Fluid Flow 25, 656–664 (2015)

    Article  MATH  Google Scholar 

  7. Wen, L.L., Zhang, H.Q.: Rogue wave solutions of the (2+1)-dimensional derivative nonlinear Schrödinger equation. Nonlinear Dyn. 86, 877–889 (2016)

    Article  MATH  Google Scholar 

  8. Miura, R.M. (ed.): Bäcklund Transformation: Lecture Notes in Mathematica, vol. 515. Springer, Berlin (1976)

    Google Scholar 

  9. Dong, H.H., Guo, B.Y., Yin, B.S.: Generalized fractional super trace identity for Hamiltonion structure of NlS–MKDV hierarchy with self consistent sources. Anal. Math. Phys. 6, 199–209 (2016)

    Article  MATH  MathSciNet  Google Scholar 

  10. Tiecheng, X., Temuer, C.: The Conservation laws and self consistent sources for a super Yang hierarchy. Nonlinear Dyn. 70, 1951–1958 (2012)

    Article  MATH  MathSciNet  Google Scholar 

  11. Boiti, M., Leon, J.P., Manna, M., Pempinelli, F.: On the spectral transform of a Korteweg–de Vries equation in two spatial dimensions. Inverse Probl. 2, 271–279 (1986)

  12. Boiti, M., Leon, J.P., Manna, M., Pempinelli, F.: On a spectral transform of a KDV-like equation related to the Schrödinger operator in the plane. Inverse Probl. 3, 25–36 (1987)

    Article  MATH  Google Scholar 

  13. Rogers, C., Konopelchenko, B.G., Stallybrass, M.P., Schief, W.K.: The Nizhnik–Veselov–Novikov equation. Associated boundary value problems. Int. J. Nonlinear Mech. 31, 441–450 (1996)

    Article  MATH  MathSciNet  Google Scholar 

  14. Radha, R., Lakshmanan, M.: Singularity analysis and Localized coherent structures in \((2+1)\) dimensional generalized Korteweg–de Vries equation. J. Math. Phys. 35, 4746–4756 (1994)

    Article  MATH  MathSciNet  Google Scholar 

  15. Kumar, C.S., Radha, R., Lashmanan, M.: Trilinearization and Localized coherent structures and periodic solutions for the \((2+1)\) dimensional KdV and NNV equations. Chaos Solitons Fractals 39, 942–955 (2009)

    Article  MATH  MathSciNet  Google Scholar 

  16. Painlevé, P.: Sur les equations différentielles du second ordre et d’ordre supérieur dont l’integrale générale est uniforme. Acta Math. 25, 1–85 (1902)

    Article  MATH  MathSciNet  Google Scholar 

  17. Weiss, J.: The Painlevé property for partial differential equations II: Bäcklund transformations, Lax pair and Schwartzian derivative. J. Math. Phys. 24, 1405–1413 (1983)

    Article  MATH  MathSciNet  Google Scholar 

  18. Estévez, P.G., Hernaéz, G.A.: Painlevé analysis and singular manifold method for a \((2+1)\) dimensional non-linear Schrödinger equation. J. Nonlinear Math. Phys. 9, 106–111 (2001)

    Article  MATH  Google Scholar 

Download references

Acknowledgements

R. S wishes to thank Department of Atomic Energy - National Board of Higher Mathematics (DAE-NBHM) for providing a Junior Research Fellowship. R. R. acknowledges DST (Grant No. SR/S2/HEP-26/2012), Council of Scientific and Industrial Research (CSIR), India (Grant 03(1323)/14/EMR-II dated 03.11.2014) and Department of Atomic Energy - National Board of Higher Mathematics (DAE-NBHM), India (Grant 2/48(21)/2014/NBHM(R.P.) /R & D II/15451) for financial support in the form of Major Research Projects. The research of P. G. E has been supported in part by MINECO (Grants MAT2013-46308 and MAT2016-75955) and Junta de Castilla y León (Grant SA226U13). P. Albares acknowledges a fellowship from the Junta de Castilla y León.

Author information

Authors and Affiliations

  1. Departamento de Física Fundamental, Universidad de Salamanca, 37008, Salamanca, Spain

    P. Albares & P. G. Estevez

  2. Centre for Nonlinear Science (CeNSc), Post-Graduate and Research Department of Physics, Government College for Women (Autonomous), Kumbakonam, 612001, India

    R. Radha & R. Saranya

  3. Post-Graduate and Research Department of Mathematics, Government College for Women (Autonomous), Kumbakonam, 612001, India

    R. Saranya

Authors
  1. P. Albares
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. P. G. Estevez
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. R. Radha
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. R. Saranya
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to R. Radha.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Albares, P., Estevez, P.G., Radha, R. et al. Lumps and rogue waves of generalized Nizhnik–Novikov–Veselov equation. Nonlinear Dyn 90, 2305–2315 (2017). https://doi.org/10.1007/s11071-017-3804-7

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11071-017-3804-7

Keywords

Search

Navigation