Analysis of connected vehicle networks using network-based perturbation techniques

Abstract

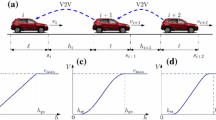
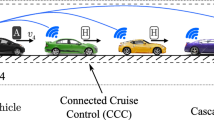
In this paper we propose a novel technique to decompose networked systems and use this technique to investigate the dynamics of connected vehicle networks with wireless vehicle-to-vehicle (V2V) communication. We apply modal perturbation analysis to approximate the modes of the perturbed network about the modes of the corresponding cyclically symmetric network. By exploiting the cyclic symmetry, we approximate the dynamics of a given mode by solving a small number of linear algebraic equations. We apply this approach to decompose connected vehicle networks into traveling waves which allows us to assess the impacts of long-range V2V communication on the stability of traffic flow.

Appendices

Appendix 1: Third-order approximation of modal dynamics

To obtain the third-order perturbation of the dynamics of the k-th mode $[\hat{\mathbf {D}}^{(1,2,3)}]^{k}_{k}$ for an arbitrary $i_{1},\sigma _{1},i_{2},\sigma _{2},i_{3},\sigma _{3}$ sextuple we take the derivative of (49) with respect to $\varepsilon _{i_{3}\sigma _{3}}$ (denoted by $\varepsilon _{3}$) which yields

$$\begin{aligned}&\mathrm {\partial }_{\varepsilon _{1}}\mathrm {\partial }_{\varepsilon _{2}} \mathrm {\partial }_{\varepsilon _{3}}\Big (\hat{\mathbf {J}}-\mathbf {I}_{N} \otimes [\hat{\mathbf {D}}]^{k}_{k}\Big )[\hat{\mathbf {T}}]_{k}\nonumber \\&\quad +\,\mathrm {\partial }_{\varepsilon _{1}}\mathrm {\partial }_{\varepsilon _{2}} \Big (\hat{\mathbf {J}}-\mathbf {I}_{N}\otimes [\hat{\mathbf {D}}]^{k}_{k}\Big ) \mathrm {\partial }_{\varepsilon _{3}}[\hat{\mathbf {T}}]_{k}\nonumber \\&\quad +\,\mathrm {\partial }_{\varepsilon _{1}}\mathrm {\partial }_{\varepsilon _{3}}\Big (\hat{ \mathbf {J}}-\mathbf {I}_{N}\otimes [\hat{\mathbf {D}}]^{k}_{k}\Big ) \mathrm {\partial }_{\varepsilon _{2}}[\hat{\mathbf {T}}]_{k}\nonumber \\&\quad +\,\mathrm {\partial }_{\varepsilon _{2}}\mathrm {\partial }_{\varepsilon _{3}} \Big (\hat{\mathbf {J}}-\mathbf {I}_{N}\otimes [\hat{\mathbf {D}}]^{k}_{k}\Big ) \mathrm {\partial }_{\varepsilon _{1}}[\hat{\mathbf {T}}]_{k}\nonumber \\&\quad +\,\mathrm {\partial }_{\varepsilon _{1}}\Big (\hat{\mathbf {J}}-\mathbf {I}_{N} \otimes [\hat{\mathbf {D}}]^{k}_{k}\Big )\mathrm {\partial }_{\varepsilon _{2}} \mathrm {\partial }_{\varepsilon _{3}}[\hat{\mathbf {T}}]_{k}\nonumber \\&\quad +\,\mathrm {\partial }_{\varepsilon _{2}}\Big (\hat{\mathbf {J}}-\mathbf {I}_{N} \otimes [\hat{\mathbf {D}}]^{k}_{k}\Big )\mathrm {\partial }_{\varepsilon _{1}} \mathrm {\partial }_{\varepsilon _{3}}[\hat{\mathbf {T}}]_{k}\nonumber \\&\quad +\,\mathrm {\partial }_{\varepsilon _{3}}\Big (\hat{\mathbf {J}}-\mathbf {I}_{N} \otimes [\hat{\mathbf {D}}]^{k}_{k}\Big )\mathrm {\partial }_{\varepsilon _{1}} \mathrm {\partial }_{\varepsilon _{2}}[\hat{\mathbf {T}}]_{k}\nonumber \\&\quad +\,\Big (\hat{\mathbf {J}}- \mathbf {I}_{N}\otimes [\hat{\mathbf {D}}]^{k}_{k}\Big )\mathrm {\partial }_{ \varepsilon _{1}}\mathrm {\partial }_{\varepsilon _{2}}\mathrm {\partial }_{\varepsilon _{3}}[ \hat{\mathbf {T}}]_{k}=0. \end{aligned}$$

(89)

At $\varepsilon _{i_{1}\sigma _{1}}=\varepsilon _{i_{2}\sigma _{2}}=\varepsilon _{i_{3}\sigma _{3}}=0$ we obtain

$$\begin{aligned}&\frac{1}{6}\mathbf {I}_{N}\otimes \Big ([\hat{\mathbf {D}}^{(1,2,3)}]^{k}_{k}+ [\hat{\mathbf {D}}^{(1,3,2)}]^{k}_{k}+[\hat{\mathbf {D}}^{(2,1,3)}]^{k}_{k}\nonumber \\&\quad +[\hat{\mathbf {D}}^{(2,3,1)}]^{k}_{k}+[\hat{\mathbf {D}}^{(3,1,2)}]^{k}_{k}+ [\hat{\mathbf {D}}^{(3,2,1)}]^{k}_{k}\Big )\nonumber \\&\quad =-\frac{1}{2}\mathbf {I}_{N}\otimes \Big ([\hat{\mathbf {D}}^{(1,2)}]^{k}_{k}+ [\hat{\mathbf {D}}^{(2,1)}]^{k}_{k}\Big )[\hat{\mathbf {T}}^{(3)}]_{k}\nonumber \\&\qquad -\frac{1}{2} \mathbf {I}_{N}\otimes \Big ([\hat{\mathbf {D}}^{(1,3)}]^{k}_{k}+[\hat{ \mathbf {D}}^{(3,1)}]^{k}_{k}\Big )[\hat{\mathbf {T}}^{(2)}]_{k}\nonumber \\&\qquad -\frac{1}{2}\mathbf {I}_{N}\otimes \Big ([\hat{\mathbf {D}}^{(2,3)}]^{k}_{k}+ [\hat{\mathbf {D}}^{(3,2)}]^{k}_{k}\Big )[\hat{\mathbf {T}}^{(1)}]_{k}\nonumber \\&\qquad +\frac{1}{2}(\hat{\mathbf {P}}^{(1)}-\mathbf {I}_{N}\otimes [\hat{\mathbf {D}}^{(1)}] ^{k}_{k})([\hat{\mathbf {T}}^{(2,3)}]_{k}+[\hat{\mathbf {T}}^{(3,2)}]_{k})\nonumber \\&\qquad +\frac{1}{2}(\hat{\mathbf {P}}^{(2)}-\mathbf {I}_{N}\otimes [\hat{\mathbf {D}}^{(2)} ]^{k}_{k})([\hat{\mathbf {T}}^{(1,3)}]_{k}+[\hat{\mathbf {T}}^{(3,1)}]_{k})\nonumber \\&\qquad + \frac{1}{2}(\hat{\mathbf {P}}^{(3)}-\mathbf {I}_{N}\otimes [ \hat{\mathbf {D}}^{(3)}]^{k}_{k})([\hat{\mathbf {T}}^{(1,2)}]_{k}+[\hat{ \mathbf {T}}^{(2,1)}]_{k})\nonumber \\&\qquad +\frac{1}{6}(\hat{\mathbf {J}}_{0}-\mathbf {I}_{N}\otimes [ \hat{\mathbf {D}}_{0}]^{k}_{k})\Big ([\hat{\mathbf {T}}^{(1,2,3)}]_{k}+[ \hat{\mathbf {T}}^{(1,3,2)}]_{k}\nonumber \\&\qquad +[\hat{\mathbf {T}}^{(2,1,3)}]_{k}+[ \hat{\mathbf {T}}^{(2,3,1)}]_{k}+[\hat{\mathbf {T}}^{(3,1,2)}]_{k}\nonumber \\&\qquad +[ \hat{\mathbf {T}}^{(3,2,1)}]_{k}\Big ). \end{aligned}$$

(90)

We can eliminate the last term in the expression above by multiplying by $[\hat{\mathbf {T}}_{0}^{-1}]^{k}$ from the left and using (26). Also because the above expression has six unknowns $\Big ($ the $[\hat{\mathbf {D}}^{(\cdot ,\cdot ,\cdot )}]^{k}_{k}$’s $\Big )$ for each $i_{1},\,\sigma _{1},\,i_{2},\,\sigma _{2},\,i_{3},\,\sigma _{3}$ sextuple we have the freedom to set

$$\begin{aligned} \begin{aligned} \hat{[\mathbf {D}}^{(1,2,3)}]^{k}_{k}=\,&[\hat{\mathbf {D}}_{3}(i_{1},\sigma _{1},i_{2},\sigma _{2},i_{3},\sigma _{3})]^{k}_{k}\\ =\,&-3[\hat{\mathbf {T}}^{-1}_{0}]^{k}(\mathbf {I}_{N}\otimes [\hat{\mathbf {D}}^{(1,2)} ]^{k}_{k})\hat{\mathbf {T}}_{0}[\hat{\mathbf {U}}^{(3)}]_{k}\\&+3[\hat{ \mathbf {T}}^{-1}_{0}]^{k}(\hat{\mathbf {P}}^{(1)}-\mathbf {I}_{N}\otimes [ \hat{\mathbf {D}}^{(1)}]^{k}_{k})\hat{\mathbf {T}}_{0}[\hat{\mathbf {U}}^{( 2,3)}]_{k}, \end{aligned} \end{aligned}$$

(91)

while the equations for the other third-order terms can be obtained by permuting on the indices corresponding to $i_{1},\,\sigma _{1},\,i_{2},\,\sigma _{2},\,i_{3},\,\sigma _{3}$ on the left and right hand side of (91). By algebraic manipulation one can show $[\hat{\mathbf {T}}^{-1}_{0}]^{k}(\mathbf {I}_{N}\otimes [\hat{\mathbf {D}}^{(1,2)}]^{k}_{k})\hat{\mathbf {T}}_{0}[\hat{\mathbf {U}}^{(3)}]_{k}=[\hat{\mathbf {T}}^{-1}_{0}]^{k}(\mathbf {I}_{N}\otimes [\hat{\mathbf {D}}^{(1)}]^{k}_{k})\hat{\mathbf {T}}_{0}[\hat{\mathbf {U}}^{(2,3)}]_{k}=0$. This means we can simplify (91) to

$$\begin{aligned}{}[\hat{\mathbf {D}}^{(1,2,3)}]^{k}_{k}=3[\hat{\mathbf {T}}^{-1}_{0}]^{k}\hat{\mathbf {P}}^{(1)}\hat{\mathbf {T}}_{0}[\hat{\mathbf {U}}^{(2,3)}]_{k}, \end{aligned}$$

(92)

and by using (17) we can obtain (62).

Appendix 2: Second-order approximation of the modal block eigenvector

Solving (59) for the connected vehicle network , we obtain the $(k,\ell )$-th block of $\hat{\mathbf {U}}^{(1,2)}$ whose elements are contained in

$$\begin{aligned} \mathbf {b}_{k\ell }^{(1,2)}=\begin{bmatrix} u^{(1,2)}_{k\ell ,11} \\ u^{(1,2)}_{k\ell ,21} \\ u^{(1,2)}_{k\ell ,12} \\ u^{(1,2)}_{k\ell ,22} \end{bmatrix}. \end{aligned}$$

(93)

For $k\ne \ell$ using (80,81) we obtain

$$\begin{aligned} \begin{aligned}&\mathbf {b}_{k\ell }^{(1,2)}=\frac{1}{p(p-\alpha \beta _{1})\eta _{k\,\ell }}\\&\times \begin{bmatrix} (p+\beta _{1}(\beta _{1}\eta _{\ell 1}-\alpha ))R(i_{1},\sigma _{1},i_{2},\sigma _{2})_{k\ell }+p\eta _{\ell 1}(p+\beta _{1}(\beta _{1}\eta _{k1}-\alpha ))Q(i_{1},\sigma _{1},i_{2},\sigma _{2})_{k\ell }-p\beta _{1}\eta _{\ell 1}S(i_{1},\sigma _{1},i_{2},\sigma _{2})_{k\ell }\\ p\eta _{\ell 1}(-\beta _{1}R(i_{1},\sigma _{1},i_{2},\sigma _{2})_{k\ell }-p\beta _{1}\eta _{k1}Q(i_{1},\sigma _{1},i_{2},\sigma _{2})_{k\ell }+pS(i_{1},\sigma _{1},i_{2},\sigma _{2})_{k\ell })\\ (-p\beta _{1}\eta _{k1}Q(i_{1},\sigma _{1},i_{2},\sigma _{2})_{k\ell }-\beta _{1}R(i_{1},\sigma _{1},i_{2},\sigma _{2})_{k\ell }+pS(i_{1},\sigma _{1},i_{2},\sigma _{2})_{k\ell })\\ p(R(i_{1},\sigma _{1},i_{2},\sigma _{2})_{k\ell }+p\eta _{k1}Q(i_{1},\sigma _{1}, i_{2},\sigma _{2})_{k\ell }-\alpha ~S(i_{1},\sigma _{1}, i_{2},\sigma _{2})_{k\;\ell }) \end{bmatrix}, \end{aligned} \end{aligned}$$

(94)

where

$$\begin{aligned} \begin{aligned} Q(i_{1},\sigma _{1},i_{2},\sigma _{2})_{k\;\ell }&=\frac{2}{N}u^{(1)}_{k\ell ,12}\Big (\mathrm {e}^{i\frac{2\pi }{N}\sigma _{2}(\ell -1)}-1\Big ),\\ R(i_{1},\sigma _{1},i_{2},\sigma _{2})_{k\;\ell }&=\frac{2}{N}\bigg (-\sum ^{N}_{j=1} \mathrm {e}^{i\frac{2\pi }{N}(i_{1}-1)(j-k)}\\&\qquad \times \Big (\mathrm {e}^{i\frac{2\pi }{N}\sigma _{1}(j-1)}-1\Big )u^{(2)}_{j\ell ,21}\bigg ),\\ S(i_{1},\sigma _{1},i_{2},\sigma _{2})_{k\;\ell }&=\frac{2}{N}\bigg (u^{(1)}_{k \ell ,22}\Big (\mathrm {e}^{i\frac{2\pi }{N}\sigma _{2}(\ell -1)}-1\Big )\\&\quad -\sum ^{N}_{j=1}\mathrm {e}^{i\frac{2\pi }{N}(i_{1}-1)(j-k)}\\&\qquad \times \Big (\mathrm {e}^{i\frac{2\pi }{N}\sigma _{1}(j-1)}-1\Big )u^{(2)}_{j\ell ,22}\bigg ). \end{aligned} \end{aligned}$$

(95)

and $u^{(1)}_{k\ell ,12},\,u^{(2)}_{j\ell ,21},\,u^{(1)}_{k\ell ,22},\,u^{(2)}_{j\ell ,22}$ are given in (77). For the case $k=\ell$ (59) has multiple possible solutions due to a nonzero nullity. In this case, we set

$$\begin{aligned} \mathbf {b}^{(1,2)}_{k\ell }=\begin{bmatrix} 0 \\ 0 \\ 0 \\ 0 \end{bmatrix}. \end{aligned}$$

(96)

Appendix 3: Cubic terms of the modal approximation

The coefficients in (82) and (83) are given by

$$\begin{aligned}&L_{0}(i_{1},\sigma _{1},i_{2},\sigma _{2},i_{3},\sigma _{3}) = \frac{1}{N^3} \frac{p\eta _{k1}}{(p-\alpha \beta _{1})^{2}}\nonumber \\&\quad \sum ^{N}_{u=1,u\ne k}\frac{(\mathrm {e}^{i\frac{2\pi }{N} \sigma _{1}(u-1)}-1)\mathrm {e}^{i\frac{2\pi }{N}(i_{1}-1)(u-k)}}{\eta _{uk}}\nonumber \\&\quad \times \bigg (-\frac{(\mathrm {e}^{i\frac{2\pi }{N}\sigma _{2}(k-1)}-1)(\mathrm {e}^{ i\frac{2\pi }{N}\sigma _{3}(k-1)}-1)\mathrm {e}^{i\frac{2\pi }{N} (i_{2}-1)(k-u)}}{\eta _{uk}}\nonumber \\&\qquad (\beta _{1}\eta _{u1}+\alpha )+\sum ^{N}_{j=1,j\ne k}\nonumber \\&\quad \frac{(\mathrm {e}^{i\frac{2\pi }{N}\sigma _{2}(j-1)}-1) (\mathrm {e}^{i\frac{2\pi }{N}\sigma _{3}(k-1)}-1)\mathrm {e}^{i \frac{2\pi }{N}(i_{2}-1)(j-u)}\mathrm {e}^{i\frac{2\pi }{N}(i_{3}-1)(k-j)}}{ \eta _{jk}}\nonumber \\&\quad (\beta _{1}\eta _{k1}+\alpha )\bigg ),\nonumber \\&\quad \mathrm {and}\nonumber \\&\quad L_{1}(i_{1},\sigma _{1},i_{2},\sigma _{2},i_{3},\sigma _{3}) = \frac{1}{N^3} \frac{1}{(p-\alpha \beta _{1})^{2}}\nonumber \\&\quad \sum ^{N}_{u=1,u\ne k}\frac{(\mathrm {e}^{ i\frac{2\pi }{N}\sigma _{1}(u-1)}-1)\mathrm {e}^{i\frac{2\pi }{N}(i_{1}-1) (u-k)}}{\eta _{uk}}\nonumber \\&\quad \times \bigg (\frac{(\mathrm {e}^{i\frac{2\pi }{N}\sigma _{2}(k-1)}-1) (\mathrm {e}^{i\frac{2\pi }{N}\sigma _{3}(k-1)}-1)\mathrm {e}^{i \frac{2\pi }{N}(i_{2}-1)(k-u)}}{\eta _{uk}}\nonumber \\&\qquad (p\eta _{u1}+\alpha ^2)-\sum ^{N}_{j=1,j\ne k}\nonumber \\&\quad \frac{(\mathrm {e}^{i\frac{2\pi }{N}\sigma _{2}(j-1)}-1)(\mathrm {e}^{ i\frac{2\pi }{N}\sigma _{3}(k-1)}-1)\mathrm {e}^{i\frac{2\pi }{N} (i_{2}-1)(j-u)}\mathrm {e}^{i\frac{2\pi }{N}(i_{3}-1)(k-j)}}{\eta _{jk}}\nonumber \\&\qquad (p\eta _{k1}+\alpha ^2)\bigg ). \end{aligned}$$

(97)

Appendix 4: Coefficients for modal stability boundaries and modal frequencies

The coefficients for $p_{k}$ and $\omega _{k}$ in (85) and (86) are obtained by plugging in (85) and (86) into (84) with $p=p_{k}$ and $\lambda =i\omega _{k}$. The zeroth-order terms in (85) and (86) are then determined by setting all $\beta _{i\sigma }=0$, taking the real and imaginary parts of (84), and solving the resulting two equations for $p_{k0}$ and $\omega _{k0}$ we obtain

$$\begin{aligned} \begin{aligned}&p_{k0}\,=\,{\textstyle \frac{1}{2}}(2\beta _{1}+\alpha )\Big ((2\beta _{1}+\alpha )\tan ^2\Big (\textstyle {\frac{\theta _{k}}{2}}\Big )+\alpha \Big ),\,\\&\omega _{k0}=(2\beta _{1}+\alpha )\tan \Big (\textstyle {\frac{\theta _{k}}{2}}\Big ), \end{aligned} \end{aligned}$$

(98)

where $\theta _{k}=\frac{2\pi }{N}(k-1)$. These expressions indeed correspond to (72) and (73).

To obtain the first-order terms for indices $i_{1},\sigma _{1}$, we take the partial derivative of (84) with respect to $\beta _{i_{1}\sigma _{1}}$ and evaluate the expression at $\beta _{i_{1}\sigma _{1}}=0$. Then taking the real and imaginary parts, and performing some algebraic manipulation we get

$$\begin{aligned} \begin{aligned} p_{k1}(i_{1},\sigma _{1})&=\frac{1}{2N}\Bigg (\omega _{k0}\bigg (\sin (\sigma _{1} \theta _{k})+\frac{2\big (1+\sin \big (\frac{\theta _{k}}{2}\big )\big )}{\sin (\theta _{k})}\\&\quad \times \big (1-\cos (\sigma _{1}\theta _{k})\big )\bigg )\\&\quad +\alpha \bigg (\frac{\sin (\sigma _{1}\theta _{k})}{\tan \big (\frac{\theta _{k}}{2}\big )}+ \big (1-\cos (\sigma _{1}\theta _{k})\big )\bigg )\Bigg )\\ \omega _{k1}(i_{1},\sigma _{1})&=\frac{1}{N}\bigg (\sin (\sigma _{1}\theta _{k}) +\tan ( \textstyle {\frac{\theta _{k}}{2}})\big (1-\cos (\sigma _{1}\theta _{k})\big )\bigg ). \end{aligned} \end{aligned}$$

(99)

Similarly, the second-order terms for the indices $i_{1},\sigma _{1},i_{2},\sigma _{2}$ can be obtained by taking the second partial derivative of (84) with respect to $\beta _{i_{1}\sigma _{1}}$ and $\beta _{i_{2}\sigma _{2}}$ and evaluating the results at $\beta _{i_{1}\sigma _{1}}=\beta _{i_{2}\sigma _{2}}=0$. Splitting the real and imaginary parts we obtain

$$\begin{aligned}&p_{k2}(i_{1},\sigma _{1},i_{2},\sigma _{2})=\frac{2}{N}\omega _{k1}(i_{1}, \sigma _{1})_{k}\frac{1-\cos (\sigma _{2}\theta _{k})}{\sin (\theta _{k})}\nonumber \\&\quad +\,\bigg (2\omega _{k0}\frac{1+\sin ^{2}\big (\frac{\theta _{k}}{2}\big )}{\sin (\theta _{k})}+ \alpha \bigg )\bigg (\mathrm {Re}\,K_{1}(i_{1},\sigma _{1},i_{2},\sigma _{2})|_{\mathrm {c}}\nonumber \\&\quad +\, \frac{1}{\omega _{k0}}\mathrm {Im}\,K_{0}(i_{1},\sigma _{1},i_{2},\sigma _{2})|_{ \mathrm {c}}\bigg )\nonumber \\&\quad +\,\bigg (\omega _{k0}+\alpha \frac{2\cos ^{2}\big (\frac{\theta _{k}}{2}\big )}{\sin (\theta _{k})}\bigg ) \bigg (-\mathrm {Im}K_{1}\,(i_{1},\sigma _{1},i_{2},\sigma _{2})|_{\mathrm {c}}\nonumber \\&\quad +\, \frac{1}{\omega _{k0}}\mathrm {Re}\,K_{0}(i_{1},\sigma _{1},i_{2},\sigma _{2})|_{ \mathrm {c}}\bigg )\nonumber \\&\omega _{k2}(i_{1},\sigma _{1},i_{2},\sigma _{2})=2\bigg (\mathrm {Re}\,K_{1}(i_{1}, \sigma _{1},i_{2},\sigma _{2})|_{\mathrm {c}}\tan \left( \textstyle {\frac{\theta _{k}}{2}}\right) \nonumber \\&\quad -\, \mathrm {Im}\,K_{1}(i_{1},\sigma _{1},i_{2},\sigma _{2})|_{\mathrm {c}}\bigg )\nonumber \\&\quad +\,\frac{2}{\omega _{k0}}\bigg (\mathrm {Re}\,K_{0}(i_{1},\sigma _{1},i_{2}, \sigma _{2})|_{\mathrm {c}}\nonumber \\&\quad +\,\mathrm {Im}\,K_{0}(i_{1},\sigma _{1},i_{2}, \sigma _{2})|_{\mathrm {c}}\tan \left( \textstyle {\frac{\theta _{k}}{2}}\right) \bigg ), \end{aligned}$$

(100)

where “$|_{\mathrm {c}}$” indicates that the quantity is evaluated with all $\beta _{i\sigma }=0$.

Finally, to obtain the third-order terms for the indices $i_{1},\sigma _{1},i_{2},\sigma _{2},i_{3},\sigma _{3}$ we take the third partial derivative of (84) with respect to $\beta _{i_{1}\sigma _{1}}$, $\beta _{i_{2}\sigma _{2}}$, and $\beta _{i_{3}\sigma _{3}}$ and evaluate the result at $\beta _{i_{1}\sigma _{1}}=\beta _{i_{2}\sigma _{2}}=\beta _{i_{3}\sigma _{3}}=0$. Taking the real and imaginary parts yields

$$\begin{aligned}&p_{k3}(i_{1},\sigma _{1},i_{2},\sigma _{2},i_{3},\sigma _{3})=3\omega _{k1}(i_{1}, \sigma _{1})\omega _{k2}(i_{1},\sigma _{1},i_{2},\sigma _{2})\nonumber \\&\quad +\,\frac{3}{N}\frac{1-\cos ( \sigma _{1}\theta _{})}{\sin (\theta _{k})}\omega _{k2}(i_{2},\sigma _{2},i_{3},\sigma _{3})\nonumber \\&\quad +\,\bigg (\frac{3}{2}\omega _{k0}+\frac{\alpha }{2}\frac{1}{\tan \big (\frac{\theta _{k}}{2}\big )} \bigg )\omega _{k3}(i_{1},\sigma _{1},i_{2},\sigma _{2},i_{3},\sigma _{3})\nonumber \\&\quad +\,6\omega _{k1}(i_{1},\sigma _{1})\bigg (\mathrm {Re}\,K_{1}(i_{2},\sigma _{2},i_{3}, \sigma _{3})|_{\mathrm {c}}\frac{1}{\tan (\theta _{k})}\nonumber \\&\quad +\,\mathrm {Im}\,K_{1}(i_{2}, \sigma _{2},i_{3},\sigma _{3})|_{\mathrm {c}}\bigg )\nonumber \\&\quad +\,6\omega _{k0}\bigg (\mathrm {\partial }_{\varepsilon _{1}}\mathrm {Re}\,K_{1}(i_{2}, \sigma _{2},i_{3},\sigma _{3})|_{\mathrm {c}}\frac{1}{\tan (\theta _{k})}\nonumber \\&\quad +\, \mathrm {\partial }_{\varepsilon _{1}}\mathrm {Im}\,K_{1}(i_{2},\sigma _{2},i_{3}, \sigma _{3})|_{\mathrm {c}}\bigg )\nonumber \\&\quad +\,6\omega _{k0}\bigg (\mathrm {Re}\,L_{1}(i_{1},\sigma _{1},i_{2},\sigma _{2},i_{3}, \sigma _{3})|_{\mathrm {c}}\frac{1}{\tan (\theta _{k})}\nonumber \\&\quad +\,\mathrm {Im}\,L_{1}(i_{1}, \sigma _{1},i_{2},\sigma _{2},i_{3},\sigma _{3})|_{\mathrm {c}}\bigg )\nonumber \\&\quad +\,6\bigg (\mathrm {\partial }_{\varepsilon _{1}}\mathrm {Im}\,K_{0}(i_{2},\sigma _{2},i_{3}, \sigma _{3})|_{\mathrm {c}}\frac{1}{\tan (\theta _{k})}\nonumber \\&\quad -\,\mathrm {\partial }_{\varepsilon _{1}} \mathrm {Re}\,K_{0}(i_{2},\sigma _{2},i_{3},\sigma _{3})|_{\mathrm {c}}\bigg )\nonumber \\&\quad +\,6\bigg (\mathrm {Im}\,L_{0}(i_{1},\sigma _{1},i_{2},\sigma _{2},i_{3},\sigma _{3})|_{ \mathrm {c}}\frac{1}{\tan (\theta _{k})}\nonumber \\&\quad -\mathrm {Re}\,L_{0}(i_{1},\sigma _{1},i_{2}, \sigma _{2},i_{3},\sigma _{3})|_{\mathrm {c}}\bigg ),\nonumber \\&\omega _{k3}(i_{1},\sigma _{1},i_{2},\sigma _{2},i_{3},\sigma _{3})=-3\frac{ \omega _{k1}(i_{1},\sigma _{1})\omega _{k2}(i_{2},\sigma _{2},i_{3},\sigma _{3})}{ \omega _{k0}}\nonumber \\&\quad +\,6\frac{\omega _{k1}(i_{1},\sigma _{1})}{\omega _{k0}}\bigg (\mathrm {Re}\,K_{1}(i_{2}, \sigma _{2},i_{3},\sigma _{3})|_{\mathrm {c}}\tan \big (\textstyle {\frac{\theta _{k}}{2}}\big )\nonumber \\&\quad -\, \mathrm {Im}\,K_{1}(i_{2},\sigma _{2},i_{3},\sigma _{3})|_{\mathrm {c}}\bigg )\nonumber \\&\quad +\,6\bigg (\mathrm {\partial }_{\varepsilon _{1}}\mathrm {Re}\,K_{1}(i_{2},\sigma _{2},i_{3}, \sigma _{3})|_{\mathrm {c}}\tan \big (\textstyle {\frac{\theta _{k}}{2}}\big )\nonumber \\&\quad -\,\mathrm {\partial }_{ \varepsilon _{1}}\mathrm {Im}\,K_{1}(i_{2},\sigma _{2},i_{3},\sigma _{3})|_{\mathrm {c}}\bigg )\nonumber \\&\quad +\,6\bigg (\mathrm {Re}\,L_{1}(i_{1},\sigma _{1},i_{2},\sigma _{2},i_{3},\sigma _{3})|_{ \mathrm {c}}\tan \big (\textstyle {\frac{\theta _{k}}{2}}\big )\nonumber \\&\quad -\,\mathrm {Im}\,L_{1}(i_{1}, \sigma _{1},i_{2},\sigma _{2},i_{3},\sigma _{3})|_{\mathrm {c}}\bigg )\nonumber \\&\quad +\,\frac{6}{\omega _{k0}}\bigg (\mathrm {\partial }_{\varepsilon _{1}}\mathrm {Re}\,K_{0}(i_{2}, \sigma _{2},i_{3},\sigma _{3})|_{\mathrm {c}}\nonumber \\&\quad +\,\mathrm {\partial }_{\varepsilon _{1}}\mathrm {Im} \,K_{0}(i_{2},\sigma _{2},i_{3},\sigma _{3})|_{\mathrm {c}}\tan (\textstyle {\frac{ \theta _{k}}{2}})\bigg )\nonumber \\&\quad +\,\frac{6}{\omega _{k0}}\bigg (\mathrm {Re}\,L_{0}(i_{1},\sigma _{1},i_{2},\sigma _{2},i_{3}, \sigma _{3})|_{\mathrm {c}}\nonumber \\&\quad +\,\mathrm {Im}\,L_{0}(i_{1},\sigma _{1},i_{2},\sigma _{2},i_{3}, \sigma _{3})|_{\mathrm {c}}\tan \big (\textstyle {\frac{\theta _{k}}{2}}\big )\bigg ). \end{aligned}$$

(101)