Skip to main content
SpringerLink
Log in

Nonlinear vibration of slightly curved pipe with conveying pulsating fluid

  • Original Paper
  • Published:
Nonlinear Dynamics Aims and scope Submit manuscript

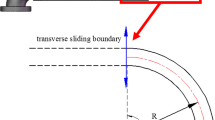
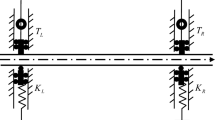
Abstract

The nonlinear governing motion equation of slightly curved pipe with conveying pulsating fluid is set up by Hamilton’s principle. The motion equation is discretized into a set of low dimensional system of nonlinear ordinary differential equations by the Galerkin method. Linear analysis of system is performed upon this set of equations. The effect of amplitude of initial deflection and flow velocity on linear dynamic of system is analyzed. Curves of the resonance responses about \(\varOmega \approx {\omega _\mathrm{{1}}}\) and \(\varOmega \approx \mathrm{{2}}{\omega _\mathrm{{1}}}\) are performed by means of the pseudo-arclength continuation technique. The global nonlinear dynamic of system is analyzed by establishing the bifurcation diagrams. The dynamical behaviors are identified by the phase diagram and Poincare maps. The periodic motion, chaotic motion and quasi-periodic motion are found in this system.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15

Similar content being viewed by others

References

  1. Paidoussis, M.P., Issid, N.: Dynamic stability of pipes conveying fluid. J. Sound Vib. 33(3), 267–294 (1974)

    Article  Google Scholar 

  2. Blevins, R.D., Saunders, H.: Flow-Induced Vibration. Van Nostrand Reinhold Co., New York (1977)

    MATH  Google Scholar 

  3. Paidoussis, M.P.: Fluid-structure Interactions: Slender Structures and Axial Flow, vol. 1. Academic press, Cambridge (1998)

    Google Scholar 

  4. Ibrahim, R.: Overview of mechanics of pipes conveying fluids-part I: fundamental studies. J. Press. Vessel Technol. 132(3), 034001 (2010)

    Article  Google Scholar 

  5. Paidoussis, M., Sundararajan, C.: Parametric and combination resonances of a pipe conveying pulsating fluid. J. Appl. Mech. 42(4), 780–784 (1975)

    Article  MATH  Google Scholar 

  6. Ariaratnam, S., Namachchivaya, N.S.: Dynamic stability of pipes conveying pulsating fluid. J. Sound Vib. 107(2), 215–230 (1986)

    Article  MATH  Google Scholar 

  7. Yoshizawa, M., Nao, H., Hasegawa, E., Tsujioka, Y.: Lateral vibration of a flexible pipe conveying fluid with pulsating flow. Bull. JSME 29(253), 2243–2250 (1986)

    Article  Google Scholar 

  8. Dang, X., Liu, W., Zheng, T.: Efficient numerical analysis for dynamic stability of pipes conveying fluids. J. Press. Vessel Technol. 111(3), 300–303 (1989)

    Article  Google Scholar 

  9. Namchchivaya, N.S.: Non-linear dynamics of supported pipe conveying pulsating fluid I. Subharmonic resonance. Int. J. Non-linear Mech. 24(3), 185–196 (1989)

    Article  MATH  Google Scholar 

  10. Namchchivaya, N.S., Tien, W.: Non-linear dynamics of supported pipe conveying pulsating fluid II. Combination resonance. Int. J. Non-linear Mech. 24(3), 197–208 (1989)

    Article  MATH  Google Scholar 

  11. Jayaraman, K., Narayanan, S.: Chaotic oscillations in pipes conveying pulsating fluid. Nonlinear Dyn. 10(4), 333–357 (1996)

    Article  Google Scholar 

  12. Panda, L., Kar, R.: Nonlinear dynamics of a pipe conveying pulsating fluid with combination, principal parametric and internal resonances. J. Sound Vib. 309(3), 375–406 (2008)

    Article  Google Scholar 

  13. Jin, J., Song, Z.: Parametric resonances of supported pipes conveying pulsating fluid. J. Fluids Struct. 20(6), 763–783 (2005)

    Article  Google Scholar 

  14. Wang, L.: A further study on the non-linear dynamics of simply supported pipes conveying pulsating fluid. Int. J. Non-linear Mech. 44(1), 115–121 (2009)

    Article  Google Scholar 

  15. Semler, C., Li, G., Paidoussis, M.: The non-linear equations of motion of pipes conveying fluid. J. Sound Vib. 169(5), 577–599 (1994)

    Article  MATH  Google Scholar 

  16. Jung, D., Chung, J., Mazzoleni, A.: Dynamic stability of a semi-circular pipe conveying harmonically oscillating fluid. J. Sound Vib. 315(1), 100–117 (2008)

    Article  Google Scholar 

  17. Yamashita, K., Nakamura, K., Yabuno, H.: Out-of-plane vibration of a curved pipe due to pulsating flow (nonlinear interactions between in-plane and out-of-plane vibrations). In: ASME 2010 3rd Joint US-European Fluids Engineering Summer Meeting collocated with 8th International Conference on Nanochannels, Microchannels, and Minichannels. American Society of Mechanical Engineers, pp. 1197–1207 (2010)

  18. Nakamura, K., Yamashita, K., Taniguchi, A., Yoshizawa, M.: Nonlinear out-of-plane vibration of a curved pipe due to pulsating flow. In: ASME 2009 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference. American Society of Mechanical Engineers, pp. 1679–1686 (2009)

  19. Ni, Q., Tang, M., Wang, Y., Wang, L.: In-plane and out-of-plane dynamics of a curved pipe conveying pulsating fluid. Nonlinear Dyn. 75(3), 603–619 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  20. Sinir, B.G.: Bifurcation and chaos of slightly curved pipes. Math. Comput. Appl. 15(3), 490–502 (2010)

    MathSciNet  MATH  Google Scholar 

  21. Wang, L., Dai, H., Qian, Q.: Dynamics of simply supported fluid-conveying pipes with geometric imperfections. J. Fluids Struct. 29, 97–106 (2012)

    Article  Google Scholar 

  22. Farshidianfar, A., Soltani, P.: Nonlinear flow-induced vibration of a SWCNT with a geometrical imperfection. Comput. Mater. Sci. 53(1), 105–116 (2012)

  23. Aghababaei, O., Nahvi, H., Ziaei-Rad, S.: Non-linear non-planar vibrations of geometrically imperfect inextensional beams, Part I: Equations of motion and experimental validation. Int. J. Non-linear Mech. 44, 147–160 (2009)

  24. Aghababaei, O., Nahvi, H., Ziaei-Rad, S.: Non-linear non-planar vibrations of geometrically imperfect inextensional beams, Part II: bifurcation analysis under base excitations. Int. J. Non-linear Mech. 44, 161–179 (2009)

  25. Love, A.E.H.A.: Treatise on Mathematical Theory of Elasticity. Dover, New York (1994)

    Google Scholar 

  26. Doedel, E.J., Champneys, A.R., Fairgrieve, T.F., Kuznetsov, Y.A., Sandstede, B., Wang, X.: Continuation and bifurcation software for ordinary differential equations (with HomCont). In: AUTO97 (1998)

  27. Semler, C., Gentleman, W., Paidoussis, M.: Numerical solutions of second order implicit non-linear ordinary differential equations. J. Sound Vib. 195(4), 553–574 (1996)

    Article  MathSciNet  MATH  Google Scholar 

Download references

Acknowledgements

This work was partly Supported by the Opening Project of Sichuan Province University Key Laboratory of Bridge Non-destruction Detecting and Engineering Computing (2016QZJ03), Sichuan University of Science & Engineering fund (2015KY02), Fund Project of Sichuan University of Science & Engineering in hit-haunting for talents (No. 2016RCL31) and Found of Science & Technology Department of Sichuan Province (Grant No. 2016JQ0046).

Author information

Authors and Affiliations

  1. School of Science, Sichuan University of Science & Engineering, Zigong, 643000, China

    Yun-dong Li

  2. School of Mechanics and Engineering, Southwest Jiaotong University, Chengdu, 610031, China

    Yi-ren Yang

Authors
  1. Yun-dong Li
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Yi-ren Yang
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Yun-dong Li.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Li, Yd., Yang, Yr. Nonlinear vibration of slightly curved pipe with conveying pulsating fluid. Nonlinear Dyn 88, 2513–2529 (2017). https://doi.org/10.1007/s11071-017-3393-5

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11071-017-3393-5

Keywords

Search

Navigation