Dual input–output pairs for modeling hysteresis inspired by mem-models

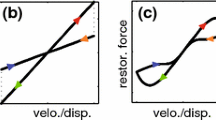
Abstract

We call attention to a dual-pair concept for modeling hysteresis involving instantaneous switching: Specifically, there are two input–output pairs for each hysteresis model under one specific input, namely a differential pair and an integral pair. Currently in engineering mechanics, only one pair is being recognized and utilized, not the other. Whereas this dual-pair concept is inherent in the differential and algebraic forms of memristors and memcapacitors, the concept has not been carried over to memristive system theory, nor to memcapacitive system theory. We show that the “zero-crossing” feature in memristors, memcapacitors, and memristive/memcapacitive models (i.e., the “mem-models”) is also a feature of the differential pairs of well-known non-mem-models, examples of which are Ramberg–Osgood, Bouc–Wen, bilinear hysteresis, and classical Preisach. The dual-pair concept thus connects mem-models and non-mem-models, thereby facilitating the modeling of hysteresis, and raising a set of scientific questions for further studies that might not otherwise come to awareness.

Appendix for Section 2

1.1 Bouc–Wen model

The formula for a Bouc-Wen (BW) model [2, 31] focusing on the auxiliary

$$\begin{aligned} \dot{r} = \left( \frac{1}{\eta }\right) \left[ A \dot{x} - \nu \left( \beta |\dot{x}| |r|^{n-1} r + \gamma \dot{x} |r|^n\right) \right] \end{aligned}$$

(30)

where $\eta$, A, $\nu$, $\beta$, $\gamma$ are model parameters, $\dot{x}$ is the velocity (r is denoted as z by many authors). A numerical example is given in Fig. 11.

Fig. 11

One Bouc–Wen model with $\eta = 10$, $A = 1$, $\nu = 1$, $\beta = 0.5$, $n = 5$, $\gamma = 0.5$ in Eq. (30) and subject to input $\dot{x} = \frac{t}{100} \sin (2\pi \frac{t}{100})$. r(t) is solved from Eq. (30) using the state-event location algorithm [26] implemented to MATLAB ode45 under “Events” option with ${{\mathrm{RelTol}}}= 10^{-6}$, ${{\mathrm{AbsTol}}}= 10^{-12}$, and ${{\mathrm{Refine}}}= 1$

We have the following pair of equations for the integral quantities:

$$\begin{aligned} x&= \int \frac{1}{\left( \frac{1}{\eta }\right) \left[ A - \nu \left( + \beta |r|^{n-1} r + \gamma |r|^n\right) \right] } {\hbox {d}}r + x_+(0),\nonumber \\&\text {when}~\dot{x} > 0 \end{aligned}$$

(31)

$$\begin{aligned} x&= \int \frac{1}{\left( \frac{1}{\eta }\right) \left[ A - \nu \left( - \beta |r|^{n-1} r + \gamma |r|^n\right) \right] } {\hbox {d}}r + x_-(0),\nonumber \\&\text {when}~\dot{x} < 0 \end{aligned}$$

(32)

In general, Eqs. (31) and (32) do not have closed-form expressions. However, it can be shown that these two integral equations define a one-to-one mapping $r \mapsto x$ like those one-to-one mappings in the algebraic forms of $p \mapsto x$ and $p \mapsto a$ for an effort-controlled memristor and memcapacitor in Tables 2 and 4, respectively. In this sense, BW is an effort-controlled model.

The differential pair is as follows:

$$\begin{aligned} \dot{x}&= \frac{1}{\left( \frac{1}{\eta }\right) \left[ A - \nu \left( + \beta |r|^{n-1} r + \gamma |r|^n\right) \right] } \dot{r}, \ \text {when}~\dot{x} {>} 0 \end{aligned}$$

(33)

$$\begin{aligned} \dot{x}&= \frac{1}{\left( \frac{1}{\eta }\right) \left[ A - \nu ( - \beta |r|^{n-1} r + \gamma |r|^n) \right] } \dot{r}, \ \text {when}~\dot{x} {<} 0 \end{aligned}$$

(34)

Adopting our notation from the effort-controlled mem-models again, we write:

$$\begin{aligned} x&= F \left( r, x_{[i]} \right) , \ \ \text {see Eqs.}\, (31) \text {and}\, (32), \,\text {for integral pair} \\ \dot{x}&= W \left( r, \text {sgn}\left( \dot{r}\right) \right) \dot{r}, \ \ \text {see Eqs.} \,(33)\, \text {and}\, (34), \nonumber \end{aligned}$$

(35)

$$\begin{aligned}&\text {for differential pair} \end{aligned}$$

(36)

where

$$\begin{aligned} x_{[i]} = x_i, \ \ i = 1, 2, 3, \ldots \end{aligned}$$

(37)

with $\dot{x} (t_i) = 0$, the velocity turning points. These are also restoring force turning points because $\dot{r} (t_i) = 0$ based on Eqs. (33) and (34).

Historically and as reviewed in [2, 11] proposed the following equation:

$$\begin{aligned} \frac{\hbox {d}{\mathcal {F}}}{\hbox {d}t} = g \left( x, {\mathcal {F}}, \text {sgn}\left( \frac{\hbox {d}x}{\hbox {d}t} \right) \right) \frac{\hbox {d}x}{\hbox {d}t} \end{aligned}$$

(38)

where ${\mathcal {F}}$ is a function representing restoring force. This equation bears similarity to Eq. (36) but is more general. Interestingly, an equation as general as Eq. (38) has not been as populated as its later development (i.e., the Bouc–Wen model) given the difficulty in deriving its explicit integral solution. The proposed differential pair for BW can thus be considered as a renewed interest in this historically important piece of work.

1.2 Bilinear hysteresis model

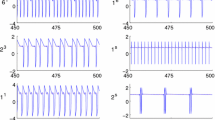
Bilinear hysteresis model [4, 5] is selected given that it can represent piecewise smooth hysteresis models defined by simple switching rules [32]. See Fig. 12 for a simulated example.

Fig. 12

One bilinear hysteresis model with two stiffness values 5 and 0.25, $r_{\text {yield}} = 0.5$, and subject to input $\dot{r}(t) = \frac{t}{1000} \sin (2\pi \frac{t}{100})$. x(t) is solved by using the state-event location algorithm [26] implemented to MATLAB ode45 under “Events” option with ${{\mathrm{RelTol}}}= 10^{-6}$ and ${{\mathrm{AbsTol}}}= 10^{-12}$, and ${{\mathrm{Refine}}}= 1$

Each piece (i.e., branch) is a straight line in (x, r). The numerical challenge of this model (indeed of any switching model) resides in treating all discontinuities (switching points)—called state events—since each discontinuity’s location in time depends on the input. In practice, the time locations of switching points are unknown and must be found in sequence as time advances. Even though there are different types of state events (see [23]), we only pay attention to one type in this dual-pair example so as to make a connection to hybrid dynamical systems.

In Fig. 12, this model shows an especially simple differential pair ($\dot{x}$, $\dot{r}$). For this piecewise linear model, even though the integral pair exhibits complicated input-dependent looping behavior, the differential pair consists of two straight lines through the origin, whose slopes are the same as the two tangent stiffness values in the integral pair.

Fig. 13

One classical Preisach model using the MATLAB GUI provided in [12] with input $r(t) = 0.0125 t \sin (t)$. The highlight is the flag-shaped hysteresis shown in the differential pairs at the lower left corner

1.3 Classical Preisach model

Classical Preisach model probably is among the most celebrated hysteresis models in engineering and beyond. Even though there is no mention of the proposed dual-pair concept, there is indeed a relevant way of thinking in the literature. For a Preisach model defined as follows in [28]:

$$\begin{aligned} B(t) = \iint _T \nu \left( h_1, h_2 \right) \gamma \left( h_1, h_2, H(t) \right) {\hbox {d}}h_1 {\hbox {d}}h_2, \end{aligned}$$

(39)

$\gamma$ represents a hysteron with switching down field $h_1$ and switching up field $h_2$, T denotes the Preisach triangle, and $\nu \left( h_1, h_2 \right)$ is the two-dimensional Preisach function. In [15, 28, 29], consecutive “turning points” of the field history are used. In [28], $\frac{\hbox {d}B}{\hbox {d}H}$, a quantity defined as dynamic permeability or susceptibility, plays an important role in circuit and electromagnetic field computation problems and can be a three-dimensional tensor.

Fig. 14

Same classical Preisach model as in Fig. 13 but subject to a different input time history of r(t), a sinusoidal wave multiplied with a windowing function as plotted. The highlight are the two minor loops demonstrating the congruency property of a classical Preisach model and their counterparts in the differential pair

“With the aid of the Preisach model, the dynamic permeability for increasing magnetic field intensity can be expressed as:

$$\begin{aligned} \frac{\hbox {d}B}{\hbox {d}H} = 2 \int _{H_r}^H \nu \left( h_1, H \right) {\hbox {d}}h_1 \end{aligned}$$

(40)

and for decreasing magnetic field intensity

$$\begin{aligned} \frac{\hbox {d}B}{\hbox {d}H} = 2 \int _H^{H_r} \nu \left( H, h_2 \right) {\hbox {d}}h_2. \end{aligned}$$

(41)

In these relations, $H_r$ is the last dominant extremum of the magnetic field intensity” [28]. A trivial manipulation involving time leads to the following symbolic expression for both increasing and decreasing situations:

$$\begin{aligned} \frac{\hbox {d}B}{\hbox {d}H} =&\frac{1+\text {sgn}\left( \dot{H}\right) }{2} W_+(H, H_r)\nonumber \\&\quad +\frac{1-\text {sgn}\left( \dot{H}\right) }{2} W_-(H, H_r) \nonumber \\&= W \left( H, \text {sgn}\left( \dot{H}\right) , H_r \right) \Rightarrow \end{aligned}$$

(42)

$$\begin{aligned} \dot{B}&= W \left( H, \text {sgn}\left( \dot{H}\right) , H_r \right) \dot{H} \end{aligned}$$

(43)

Following Chapter 11 in [16], B and H may be analogous to x and r, respectively. Adopting the mem-model notation (again), we write:

$$\begin{aligned}&\dot{x} = W \left( r, \text {sgn}\left( \dot{r}\right) , r_{[i]} \right) \dot{r}, \ \ \text {for differential pair} \end{aligned}$$

(44)

$$\begin{aligned}&x = F \left( r, \text {sgn}\left( \dot{r}\right) , r_{[i]} \right) , \ \ \text {for integral pair} \end{aligned}$$

(45)

where $r_{[i]}$ denotes the last dominant extremum of r.

To further validate the proposed dual-pair concept, numerical examples given in Figs. 13 and 14 are for one classical Preisach model under two different piecewise monotonic inputs. Using piecewise monotonic inputs is not uncommon for Preisach models, e.g., the congruency property is proved by considering a monotonically increasing/decreasing input [19].