Skip to main content
SpringerLink
Log in

Synchronization behavior of coupled neuron circuits composed of memristors

  • Original Paper
  • Published:
Nonlinear Dynamics Aims and scope Submit manuscript

Abstract

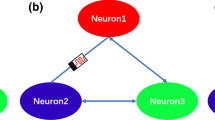
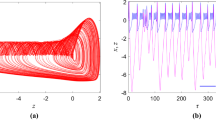
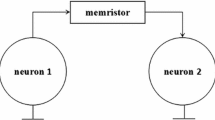
The fluctuation of intracellular and extracellular ion concentration induces the variation of membrane potential, and also complex distribution of electromagnetic field is generated. Furthermore, the membrane potential can be modulated by time-varying electromagnetic field. Therefore, magnetic flux is proposed to model the effect of electromagnetic induction in case of complex electrical activities of cell, and memristor is used to connect the coupling between membrane potential and magnetic flux. Based on the improved neuron model with electromagnetic induction being considered, the bidirectional coupling-induced synchronization behaviors between two coupled neurons are investigated on Spice tool and also printed circuit board. It is found that electromagnetic induction is helpful for discharge of neurons under positive feedback coupling, while electromagnetic induction is necessary to enhance synchronization behaviors of coupled neurons under negative feedback coupling. The frequency analysis on isolate neuron confirms that the frequency spectrum is enlarged under electromagnetic induction, and self-induction effect is detected. These experimental results can be helpful for further dynamical analysis on synchronization of neuronal network subjected to electromagnetic radiation.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8

Similar content being viewed by others

References

  1. Hodgkin, A.L., Huxley, A.F.: A quantitative description of membrane current and its application to conduction and excitation in nerve. J. Physiol. 117, 500–544 (1952)

    Article  Google Scholar 

  2. Ader, C., Schneider, R., Hornig, S., et al.: A structural link between inactivation and block of a K\(^{+}\) channel. Nat. Struct. Molec. Biol. 15, 605–612 (2008)

    Article  Google Scholar 

  3. Fleidervish, I.A., Libman, L., Katz, E., et al.: Endogenous polyamines regulate cortical neuronal excitability by blocking voltage-gated Na\(^{+}\) channels. PNAS 105, 18994–18999 (2008)

    Article  Google Scholar 

  4. Gong, Y.B., Hao, Y.H., Xie, Y.H.: Channel block-optimized spiking activity of Hodgkin-Huxley neurons on random networks. Phys. A 389, 349–357 (2010)

    Article  Google Scholar 

  5. Liu, S.B., Wu, Y., Li, J.J., et al.: The dynamic behavior of spiral waves in stochastic Hodgkin-Huxley neuronal networks with ion channel blocks. Nonlinear Dyn. 73, 1055–1063 (2013)

    Article  MathSciNet  Google Scholar 

  6. Ozer, M., Perc, M., Uzuntarla, M.: Controlling the spontaneous spiking regularity via channel blocking on Newman-Watts networks of Hodgkin-Huxley neurons. EPL 86, 40008 (2009)

    Article  Google Scholar 

  7. Wang, B.Y., Gong, Y.B.: Effects of channel noise on synchronization transitions in delayed scale-free network of stochastic Hodgkin-Huxley neurons. Chin. Phys. B 24, 0118702 (2014)

    Article  Google Scholar 

  8. Sun, X.J., Shi, X.: Effects of channel blocks on the spiking regularity in clustered neuronal networks. Sci. China Technol. Sci. 57, 884–897 (2014)

    Google Scholar 

  9. Huang, Y.D., Li, X., Shuai, J.W.: Langevin approach with rescaled noise for stochastic channel dynamics in Hodgkin-Huxley neurons. Chin. Phys. B 24, 120501 (2015)

    Article  Google Scholar 

  10. Qiu, K., Tang, J., Ma, J., et al.: Controlling intracellular Ca\(^{2+}\) spiral waves by the local agonist in the cell membrane. Chin. Phys. B 19, 030508 (2010)

    Article  Google Scholar 

  11. Hindmarsh, J.L., Rose, R.M.: A model of the nerve impulse using two first-order differential equations. Nature 296, 162–164 (1982)

    Article  Google Scholar 

  12. Herz, A.V.M., Gollisch, T., Machens, C.K., et al.: Modeling single-neuron dynamics and computations: a balance of detail and abstraction. Science 314, 80–85 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  13. Izhikevich, E.M.: Which model to use for cortical spiking neurons? IEEE Trans. Neural Netw. 15, 1063–1070 (2004)

    Article  Google Scholar 

  14. Gu, H.G., Pan, B.B.: A four-dimensional neuronal model to describe the complex nonlinear dynamics observed in the firing patterns of a sciatic nerve chronic constriction injury model. Nonlinear Dyn. 81, 2107–2126 (2015)

    Article  MathSciNet  Google Scholar 

  15. Ibarz, B., Casado, J.M., Sanjuán, M.A.F.: Map-based models in neuronal dynamics. Phys. Rep. 501, 1–74 (2011)

    Article  Google Scholar 

  16. Wang, C.N., He, Y.J., Ma, J., et al.: Parameters estimation, mixed synchronization, and antisynchronization in Chaotic Systems. Complexity 20, 64–73 (2014)

    Article  MathSciNet  Google Scholar 

  17. Ma, J., Xu, Y., Wang, C.N., et al.: Pattern selection and self-organization induced by random boundary initial values in a neuronal network. Phys. A 461, 586–594 (2016)

    Article  MathSciNet  Google Scholar 

  18. Song, X.L., Wang, C.N., Ma, J., et al.: Collapse of ordered spatial pattern in neuronal network. Phys. A 451, 95–112 (2016)

    Article  MathSciNet  Google Scholar 

  19. Ma, J., Tang, J.: A review for dynamics of collective behaviors of network of neurons. Sci. China Technol. Sci. 58, 2038–2045 (2015)

    Article  Google Scholar 

  20. Ma, J., Xu, J.: An introduction and guidance for neurodynamics. Sci. Bull. 60, 1969–1971 (2015)

    Article  Google Scholar 

  21. Wang, H.T., Chen, Y.: Firing dynamics of an autaptic neuron. Chin. Phys. B 24, 0128709 (2015)

    Article  Google Scholar 

  22. Song, X.L., Wang, C.N., Ma, J., et al.: Transition of electric activity of neurons induced by chemical and electric autapses. Sci. China Technol. Sci. 58, 1007–1014 (2015)

    Article  Google Scholar 

  23. Yilmaz, E., Baysal, V., Ozer, M., et al.: Autaptic pacemaker mediated propagation of weak rhythmic activity across small-world neuronal networks. Phys. A 444, 538–546 (2016)

    Article  MathSciNet  Google Scholar 

  24. Herrmann, C.S., Klaus, A.: Autapse turns neuron into oscillator. Int. J. Bifurc. Chaos 14, 623–633 (2004)

    Article  MathSciNet  MATH  Google Scholar 

  25. Guo, D.Q., Chen, M.M., Perc, M., et al.: Firing regulation of fast-spiking interneurons by autaptic inhibition. EPL 114, 30001 (2016)

    Article  Google Scholar 

  26. Ren, G.D., Wu, G., Ma, J., et al.: Simulation of electric activity of neuron by setting up a reliable neuronal circuit driven by electric autapse. Acta Phys. Sin. 64, 058702 (2015)

    Google Scholar 

  27. Ma, J., Song, X.L., Jin, W.Y., et al.: Autapse-induced synchronization in a coupled neuronal network. Chaos Solitons Fract. 80, 31–38 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  28. Ma, J., Qin, H.X., Song, X.L., et al.: Pattern selection in neuronal network driven by electric autapses with diversity in time delays. Int. J. Mod. Phys. B 29, 1450239 (2015)

    Article  Google Scholar 

  29. Qin, H.X., Wu, Y., Wang, C.N., et al.: Emitting waves from defects in network with autapses. Commun. Nonlinear Sci. Numer. Simulat. 23(1), 164–174 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  30. Yi, G.S., Wang, J., Tsang, K.M., et al.: Spike-frequency adaptation of a two compartment neuron modulated by extracellular electric fields. Biol. Cybern. 109, 287–306 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  31. Yi, G.S., Wang, J., Han, C.X., et al.: Spiking patterns of a minimal neuron to ELF sinusoidal electric field. Appl. Math. Model 36, 3673–3684 (2012)

    Article  Google Scholar 

  32. Akiyama, H., Shimizu, Y., Miyakawa, H., et al.: Extracellular DC electric fields induce nonuniform membrane polarization in rat hippocampal CA1 pyramidal neurons. Brain Res. 1383, 22–35 (2011)

  33. Li, J.J., Liu, S.B., Liu, W.M., et al.: Suppression of firing activities in neuron and neurons of network induced by electromagnetic radiation. Nonlinear Dyn. 83, 801–810 (2016)

    Article  MathSciNet  Google Scholar 

  34. Lv, M., Ma, J.: Model of electrical activity in a neuron under magnetic flow effect. Nonlinear Dyn. 85, 1479–1490 (2016)

    Article  Google Scholar 

  35. Lv, M., Ma, J.: Multiple modes of electrical activities in a new neuron model under electromagnetic radiation. Neurocomputing 205, 375–381 (2016)

  36. Li, Q.D., Tang, S., Zeng, H.Z., et al.: On hyperchaos in a small memristive neural network. Nonlinear Dyn. 78, 1087–1099 (2014)

    Article  MATH  Google Scholar 

  37. Pham, V.T., Jafari, S., Vaidyanathan, S., et al.: A novel memristive neural network with hidden attractors and its circuitry implementation. Sci. China Technol. Sci. 59, 358–363 (2016)

    Article  Google Scholar 

  38. Cafagna, D., Grassi, G.: On the simplest fractional-order memristor-based chaotic system. Nonlinear Dyn. 70, 1185–1197 (2012)

    Article  MathSciNet  Google Scholar 

  39. Yuan, F., Wang, G.Y., Wang, X.Y.: Dynamical characteristics of an HP memristor based on an equivalent circuit model in a chaotic oscillator. Chin. Phys. B 24, 060506 (2015)

    Article  Google Scholar 

  40. Ma, J., Chen, Z.Q., Wang, Z.L., et al.: A four-wing hyper-chaotic attractor generated from a 4-D memristive system with a line equilibrium. Nonlinear Dyn. 81, 1275–1288 (2015)

    Article  MATH  Google Scholar 

  41. Chen, M., Li, M.Y., Yu, Q., et al.: Dynamics of self-excited attractors and hidden attractors in generalized memristor-based Chua’s circuit. Nonlinear Dyn. 81, 215–226 (2015)

    Article  MathSciNet  Google Scholar 

  42. Sabarathinam, S., Volos, C.K., Thamilmaran, K.: Implementation and study of the nonlinear dynamics of a memristor-based duffing oscillator. Nonlinear Dyn. (2016). doi:10.1007/s11071-016-3022-8

Download references

Acknowledgements

This work is supported by National Natural Science Foundation of China under Grant Nos. 11365014 and 11372122 and also supported by the Gansu National Science of Foundation under Grant No. 1506RJZA095.

Author information

Authors and Affiliations

  1. Department of Physics, Lanzhou University of Technology, Lanzhou, 730050, China

    Guodong Ren, Ying Xu & Chunni Wang

  2. NAAM-Research Group, Department of Mathematics, Faculty of Science, King Abdulaziz University, P.O.Box 80203, Jeddah, 21589, Saudi Arabia

    Chunni Wang

Authors
  1. Guodong Ren
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Ying Xu
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Chunni Wang
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Chunni Wang.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Ren, G., Xu, Y. & Wang, C. Synchronization behavior of coupled neuron circuits composed of memristors. Nonlinear Dyn 88, 893–901 (2017). https://doi.org/10.1007/s11071-016-3283-2

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11071-016-3283-2

Keywords

Search

Navigation