On the formation of hidden chaotic attractors and nested invariant tori in the Sprott A system

Abstract

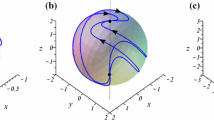
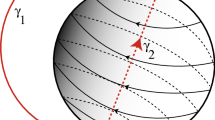
We consider the well-known Sprott A system, which depends on a single real parameter a and, for $a=1$, was shown to present a hidden chaotic attractor. We study the formation of hidden chaotic attractors as well as the formation of nested invariant tori in this system, performing a bifurcation analysis by varying the parameter a. We prove that, for $a=0$, the Sprott A system has a line of equilibria in the z-axis, the phase space is foliated by concentric invariant spheres with two equilibrium points located at the south and north poles, and each one of these spheres is filled by heteroclinic orbits of south pole–north pole type. For $a\ne 0$, the spheres are no longer invariant algebraic surfaces and the heteroclinic orbits are destroyed. We do a detailed numerical study for $a>0$ small, showing that small nested invariant tori and a limit set, which encompasses these tori and is the $\alpha$- and $\omega$-limit set of almost all orbits in the phase space, are formed in a neighborhood of the origin. As the parameter a increases, this limit set evolves into a hidden chaotic attractor, which coexists with the nested invariant tori. In particular, we find hidden chaotic attractors for $a<1$. Furthermore, we make a global analysis of Sprott A system, including the dynamics at infinity via the Poincaré compactification, showing that for $a>0$, the only orbit which escapes to infinity is the one contained in the z-axis and all other orbits are either homoclinic to a limit set (or to a hidden chaotic attractor, depending on the value of a), or contained on an invariant torus, depending on the initial condition considered.