Skip to main content
SpringerLink
Log in

Bifurcation, periodic and chaotic motions of the modified equal width-Burgers (MEW-Burgers) equation with external periodic perturbation

  • Original Paper
  • Published:
Nonlinear Dynamics Aims and scope Submit manuscript

Abstract

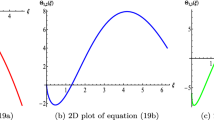
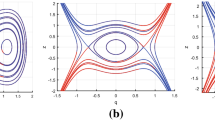
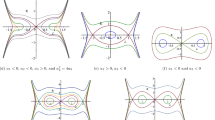
The modified equal width-Burgers (MEW-Burgers) equation is introduced for the first time. The bifurcation behavior of the MEW-Burgers equation is studied. Considering an external periodic perturbation, the periodic and chaotic motions of the perturbed MEW-Burgers equation are investigated by using phase projection analysis, time series analysis, Poincaré section and bifurcation diagram. The strength (\(f_0\)) of the external periodic perturbation plays a crucial role in the periodic and chaotic motions of the perturbed MEW-Burgers equation.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16

Similar content being viewed by others

References

  1. Gardner, C.S., Greene, J.M., Kruskal, M.D., Miura, R.M.: Method for solving the Korteweg-de Vries equation. Phys. Rev. Lett. 19, 1095–1097 (1967)

    Article  MATH  Google Scholar 

  2. Evans, D.J., Raslan, K.R.: Solitary waves for the generalized equal width (GEW) equation. Int. J. Comput. Math. 82(4), 445–455 (2005)

    Article  MathSciNet  MATH  Google Scholar 

  3. Yu, J., Lou, S.Y.: Deformation and (3+1)-dimensional integrable model. Sci. China (Ser. A) 43, 655–660 (2000)

    Article  MathSciNet  MATH  Google Scholar 

  4. Lou, S.Y.: Searching for higher dimensional integrable models from lower ones via Painleve analysis. Phys. Rev. Lett. 80, 5027–5031 (1998)

    Article  MathSciNet  MATH  Google Scholar 

  5. Nguetcho, A.S.T., Jibin, L., Bilbault, J.M.: Bifurcations of phase portraits of a Singular Nonlinear Equation of the Second Class. Commun. Nonlinear Sci. Numer. Simul. 19(8), 2590–2601 (2014)

    Article  MathSciNet  Google Scholar 

  6. Horikawa, Y., Kitajima, H.: Quasiperiodic and exponential transient phase waves and their bifurcations in a ring of unidirectionally coupled parametric oscillators. Nonlinear Dyn. 70(2), 1079–1094 (2012)

    Article  MathSciNet  Google Scholar 

  7. Mohebbi, A.: Solitary wave solutions of the nonlinear generalized Pochhammer–Chree and regularized long wave equations. Nonlinear Dyn. 70(4), 2463–2474 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  8. Abdullaev, F.K.: Dynamical chaos of solitons and nonlinear periodic waves. Phys. Rep. 179, 1–78 (1989)

    Article  MathSciNet  Google Scholar 

  9. Grimshaw, R., Tian, X.: Periodic and chaotic behaviour in a reduction of the perturbed Korteweg-de Vries equation. Proc. R. Soc. Lond. A 455, 1–21 (1994)

    Article  MathSciNet  MATH  Google Scholar 

  10. Zheng, D.J., Yeh, W.J., Symko, O.G.: Periodic doubling in a perturbed sine-Gordon system. Phys. Lett. A 140, 225–228 (1989)

    Article  Google Scholar 

  11. Blyuss, K.B.: Chaotic behaviour of solutions to a perturbed Korteweg-de Vries equation. Rep. Math. Phys. 49, 29–38 (2002)

    Article  MathSciNet  MATH  Google Scholar 

  12. Moon, H.T.: Homoclinic crossings and pattern selection. Phys. Rev. Lett. 64, 412–414 (1990)

    Article  Google Scholar 

  13. Morrison, P.J., Meiss, J.D., Carey, J.R.: Scattering of RLW solitary waves. Phys. D 11, 324–336 (1984)

    Article  MathSciNet  MATH  Google Scholar 

  14. Pregrine, D.H.: Calculations of the development of an undular bore. J. Fluid Mech. 25, 321–330 (1966)

    Article  Google Scholar 

  15. Abdulloev, K.O., Bogolubsky, I.L., Markhankv, V.G.: One more example of inelastic soliton interaction. Phys. Lett. 56A, 427–428 (1976)

    Article  MathSciNet  Google Scholar 

  16. Zaki, S.I.: Solitary wave interactions for the modified equal width equation. Comput. Phys. Commun. 126, 219–231 (2000)

    Article  MATH  Google Scholar 

  17. Wazwaz, A.M.: The tanh and sine-cosine methods for a reliable treatment of the modified equal width equation and its variants. Commun. Nonlinear Sci. Numer. Simul. 11, 148–160 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  18. Saha, A.: Bifurcation of travelling wave solutions for the generalized KP-MEW equations. Commun. Nonlinear Sci. Numer. Simul. 17, 3539–3551 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  19. Saha, A., Prasad, P.K.: A study on bifurcations of traveling wave solutions for the generalized Zakharov–Kuznetsov modified equal width equation. Int. J. Pure Appl. Math. 87(6), 795–808 (2013)

    Article  Google Scholar 

  20. Jannat, N., Ferdousi, M., Mamun, A.A.: Ion-acoustic shock waves in nonextensive multi-ion plasmas. Commun. Theor. Phys. 64, 479–484 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  21. Ferdousi, M., Miah, M.R., Sultana, S., Mamun, A.A.: Dust-acoustic shock waves in an electron depleted nonextensive dusty plasmas. Astrophys. Space Sci. 360, 43 (2015)

  22. Ema, S.A., Ferdousi, M., Sultana, S., Mamun, A.A.: Dust-ion-acoustic shock waves in nonextensive dusty multi-ion plasmas. Eur. Phys. J. Plus 130, 46 (2015)

    Article  Google Scholar 

  23. Uddin, M.J., Alam, M.S., Mamun, A.A.: Positron-acoustic shock waves associated with cold viscous positron fluid in superthermal electron-positron-ion plasmas. Phys. Plasmas 22, 062111 (2015)

    Article  MATH  Google Scholar 

  24. Pakzad, H.R.: Dust acoustic solitary and shock waves in coupled dusty plasmas with variable dust charge and vortex-like ion distribution. Astrophys. Space Sci. 330, 301–310 (2010)

    Article  MATH  Google Scholar 

  25. Bains, A.S., Tribeche, M.: Oblique shock dynamics in nonextensive magnetized plasma. Astrophys. Space Sci. 351, 191–195 (2014)

    Article  Google Scholar 

  26. Lakshmanan, M., Rajasekar, S.: Nonlinear Dynamics. Springer, Heidelberg (2003)

    Book  MATH  Google Scholar 

  27. Nieto, J.J., Tores, A.: A nonlinear biomathematical model for the study of intracranial aneurysms. J. Neurol. Sci. 177, 18–23 (2000)

    Article  Google Scholar 

  28. Guckenheimer, J., Holmes, P.J.: Nonlinear Oscillations, Dynamical Systems and Bifurcations of Vector Fields. Springer, New York (1983)

    Book  MATH  Google Scholar 

  29. Zhang, J.Y., Feng, B.Y.: Geometric Theory in Ordinary Differential Equations and Bifurcation, 2nd edn. Peking University Press, Beijing (2000)

    Google Scholar 

  30. Dubinov, A.E., Kolotkov, D.Y., Sazonkin, M.A.: Supernonlinear waves in plasma. Plasma Phys. Rep. 38(10), 833–844 (2012)

    Article  Google Scholar 

  31. Molenaar, D., Clercx, H.J.H., van Heijst, G.J.F.: Transition to chaos in a confined two-dimensional fluid flow. Phys. Rev. Lett. 95, 104503 (2005)

    Article  Google Scholar 

Download references

Acknowledgements

The author of this article would like to thank the Editor and reviewers for their valuable suggestions and comments which helped to improve the paper.

Author information

Authors and Affiliations

  1. Department of Mathematics, Sikkim Manipal Institute of Technology, Sikkim Manipal University, Majitar, Rangpo, East-Sikkim, 737136, India

    Asit Saha

Authors
  1. Asit Saha
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Asit Saha.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Saha, A. Bifurcation, periodic and chaotic motions of the modified equal width-Burgers (MEW-Burgers) equation with external periodic perturbation. Nonlinear Dyn 87, 2193–2201 (2017). https://doi.org/10.1007/s11071-016-3183-5

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11071-016-3183-5

Keywords

Search

Navigation