Skip to main content
SpringerLink
Log in

Study of hidden attractors, multiple limit cycles from Hopf bifurcation and boundedness of motion in the generalized hyperchaotic Rabinovich system

  • Original Paper
  • Published:
Nonlinear Dynamics Aims and scope Submit manuscript

Abstract

Based on Rabinovich system, a 4D Rabinovich system is generalized to study hidden attractors, multiple limit cycles and boundedness of motion. In the sense of coexisting attractors, the remarkable finding is that the proposed system has hidden hyperchaotic attractors around a unique stable equilibrium. To understand the complex dynamics of the system, some basic properties, such as Lyapunov exponents, and the way of producing hidden hyperchaos are analyzed with numerical simulation. Moreover, it is proved that there exist four small-amplitude limit cycles bifurcating from the unique equilibrium via Hopf bifurcation. Finally, boundedness of motion of the hyperchaotic attractors is rigorously proved.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Fig. 1
Fig. 2
Fig. 3
Fig. 4

Similar content being viewed by others

References

  1. Sprott, J.C.: Chaos and Time Series Analysis. Oxford University Press, Oxford (2003)

    MATH  Google Scholar 

  2. Lorenz, E.N.: Deterministic non-periodic flow. J. Atmos. Sci. 20, 130–141 (1963)

    Article  Google Scholar 

  3. Sprott, J.C.: A dynamical system with a strange attractor and invariant tori. Phys. Lett. A 378, 1361–1363 (2014)

    Article  MathSciNet  Google Scholar 

  4. Sprott, J.C., Wang, X., Chen, G.: When two dual chaotic systems shake hands. Int. J. Bifurc. Chaos 24, 1450086 (2014)

    Article  MathSciNet  Google Scholar 

  5. Li, C., Sprott, J.C.: Multistability in the Lorenz system: a broken butterfly. Int. J. Bifurc. Chaos 24, 1450131 (2014)

    Article  MathSciNet  Google Scholar 

  6. Wei, Z., Zhang, W.: Hidden attractors and dynamical behaviors in an extended Rikitake system. Int. J. Bifurc. Chaos 24, 1550028 (2015)

    Article  MathSciNet  Google Scholar 

  7. Wu, G., Baleanu, D.: Discrete fractional logistic map and its chaos. Nonlinear Dyn. 75, 283–287 (2014)

  8. Huang, C., Cao, J.: Hopf bifurcation in an n-dimensional Goodwin model via multiple delays feedback. Nonlinear Dyn. 79, 2541–2552 (2014)

    Article  MathSciNet  Google Scholar 

  9. Boulkroune, A., Bouzeriba, A., Hamel, S., Bouden, T.: A projective synchronization scheme based on fuzzy adaptive control for unknown multivariable chaotic systems. Nonlinear Dyn. 78, 433–447 (2014)

    Article  MathSciNet  Google Scholar 

  10. Boulkroune, A., Bouzeriba, A., Hamel, S., Bouden, T.: Adaptive fuzzy control-based projective synchronization of uncertain nonaffine chaotic systems. Complexity (2014). doi:10.1002/cplx.21596

  11. Boulkroune, A., Msaad, M.: Fuzzy adaptive observer-based projective synchronization for nonlinear systems with input nonlinearity. J. Vib. Control 18, 437–450 (2012)

    Article  MathSciNet  Google Scholar 

  12. Silva, C.P.: Sil’nikov theorem—a tutorial. IEEE Trans. Circuits Syst. I 40, 657–682 (1993)

    Article  Google Scholar 

  13. Zhou, T., Chen, G.: Classification of chaos in 3-D autonomous quadratic systems-I: basic framework and methods. Int. J. Bifurc. Chaos 16, 2459–2479 (2006)

    Article  MATH  Google Scholar 

  14. Leonov, G.A., Kuznetsov, N.V.: Hidden attractors in dynamical systems: from hidden oscillations in Hilbert–Kolmogorov, Aizerman, and Kalman problems to hidden chaotic attractor in Chua circuits. Int. J. Bifurc. Chaos 23, 1330002 (2013)

    Article  MathSciNet  Google Scholar 

  15. Leonov, G.A., Kuznetsov, N.V., Vagaitsev, V.I.: Localization of hidden Chua’s attractors. Phys. Lett. A 375, 2230–2233 (2011)

  16. Leonov, G.A., Kuznetsov, N.V., Vagaitsev, V.I.: Hidden attractor in smooth Chua systems. Phys. D 241, 1482–1486 (2012)

    Article  MATH  MathSciNet  Google Scholar 

  17. Wei, Z.: Dynamical behaviors of a chaotic system with no equilibria. Phys. Lett. A 376, 102–108 (2011)

    Article  MATH  MathSciNet  Google Scholar 

  18. Jafari, S., Sprott, J.C., Golpayegani, S.M.R.H.: Elementary quadratic chaotic flows with no equilibria. Phys. Lett. A 377, 699–702 (2013)

    Article  MathSciNet  Google Scholar 

  19. Wang, X., Chen, G.: A chaotic system with only one stable equilibrium. Commun. Nonlinear Sci. Numer. Simul. 17, 1264–1272 (2012)

    Article  MathSciNet  Google Scholar 

  20. Wei, Z., Yang, Q.: Dynamical analysis of a new autonomous 3-D chaotic system only with stable equilibria. Nonlinear Anal.: Real World Appl. 12, 106–118 (2011)

    Article  MATH  MathSciNet  Google Scholar 

  21. Wei, Z., Yang, Q.: Dynamical analysis of the generalized Sprott C system with only two stable equilibria. Nonlinear Dyn. 68, 543–554 (2012)

    Article  MATH  MathSciNet  Google Scholar 

  22. Molaie, M., Jafari, S., Sprott, J.C., Golpayegani, S.M.R.H.: Simple chaotic flows with one stable equilibrium. Int. J. Bifurc. Chaos 23, 1350188 (2013)

    Article  Google Scholar 

  23. Sprott, J.C., Wang, X., Chen, G.: Coexistence of point, periodic and strange attractors. Int. J. Bifurc. Chaos 23, 1350093 (2013)

    Article  MathSciNet  Google Scholar 

  24. Wang, Z., Cang, S., Ochola, E.O., Sun, Y.: A hyperchaotic system without equilibrium. Nonlinear Dyn. 69, 531–537 (2012)

    Article  MathSciNet  Google Scholar 

  25. Li, C., Sprott, J.C.: Coexisting hidden attractors in a 4-D simplified Lorenz system. Int. J. Bifurc. Chaos 24, 1450034 (2014)

    Article  MathSciNet  Google Scholar 

  26. Pham, V.T., Volos, V., Jafari, S., Wei, Z., Wang, X.: Constructing a novel no-equilibrium chaotic system. Int. J. Bifurc. Chaos 24, 1450073 (2014)

    Article  MathSciNet  Google Scholar 

  27. Wei, Z., Wang, R., Liu, A.: A new finding of the existence of hidden hyperchaotic attractors with no equilibria. Math. Comput. Simul. 100, 13–23 (2014)

    Article  MathSciNet  Google Scholar 

  28. Mahmoud, G.M., Mahmoud, E.E., Ahmed, M.E.: On the hyperchaotic complex Lü system. Nonlinear Dyn. 58, 725–738 (2009)

    Article  MATH  MathSciNet  Google Scholar 

  29. Li, F., Jin, Y.: Hopf bifurcation analysis and numerical simulation in a 4D-hyperchaotic system. Nonlinear Dyn. 67, 2857–2864 (2012)

    Article  MATH  MathSciNet  Google Scholar 

  30. Saberi, N.H., Gorder, R.A.V.: Competitive modes for Baier–Sahle hyperchaotic flow in arbitrary dimensions. Nonlinear Dyn. 74, 581–590 (2013)

    Article  MATH  Google Scholar 

  31. Chen, Y., Yang, Q.: Dynamics of a hyperchaotic Lorenz-type system. Nonlinear Dyn. 77, 569–581 (2014)

    Article  Google Scholar 

  32. Guckenheimer, J., Holmes, P.: Nonlinear Oscillations, Dynamical Systems, and Bifurcations of Vector Fields. Springer, New York (1983)

    Book  MATH  Google Scholar 

  33. Kuznetsov, Y.A.: Elements of Applied Bifurcation Theory, 2nd edn. Springer, New York (1998)

    MATH  Google Scholar 

  34. Yu, P.: Computation of normal forms via a perturbation technique. J. Sound Vib. 211, 19–38 (1998)

    Article  MATH  Google Scholar 

  35. Yu, Pei: Closed-form conditions of bifurcation points for general differential equations. Int. J. Bifurc. Chaos 15, 1467 (2005)

    Article  MATH  Google Scholar 

  36. Yu, P., Han, M.: Small limit cycles bifurcating from fine focus points in cubic order \(Z_2\)-equivariant vector fields. Chaos Solut. Fract. 24, 329–348 (2005)

    Article  MATH  MathSciNet  Google Scholar 

  37. Llibre, J., Zhang, X.: Hopf bifurcation in higher dimensional differential systems via the averaging method. Pac. J. Math. 240, 321–341 (2009)

    Article  MATH  MathSciNet  Google Scholar 

  38. Han, M., Yu, P.: Normal Forms, Melnikov Functions, and Bifurcations of Limit Cycles. Springer, New York (2012)

    Book  MATH  Google Scholar 

  39. Tian, Y., Yu, P.: An explicit recursive formula for computing the normal forms associated with semisimple cases. Commun. Nonlinear Sci. Numer. Simul. 19(7), 2294–2308 (2014)

    Article  MathSciNet  Google Scholar 

  40. Llibre, J., Valls, C.: Hopf bifurcation for some analytic differential systems in \(R^3\) via averaging theory. Discret. Contin. Dyn. Syst. Ser. B 30, 779–790 (2011)

    Article  MATH  MathSciNet  Google Scholar 

  41. Llibre, J., Chavela, E.P.: Zero-Hopf bifurcation for a class of Lorenz-type systems. Discret. Contin. Dyn. Syst. Ser. B 19, 1731–1736 (2014)

    Article  MATH  Google Scholar 

  42. Pikovsky, A.S., Rabinovich, M.I., Traktengerts, V.Y.: Onset of stochasticity in decay confinement of parametric instability. Sov. Phys. JETP 47, 715–719 (1978)

    Google Scholar 

  43. Llibre, J., Messias, M., da Silva, P.R.: On the global dynamics of the Rabinovich system. J. Phys. A: Math. Theor. 41, 275210 (2008)

  44. Liu, Y., Yang, Q., Pang, Q.: A hyperchaotic system from the Rabinovich system. J. Comput. Appl. Math. 234, 101–113 (2010)

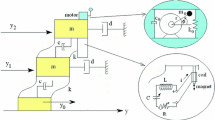
    Article  MATH  MathSciNet  Google Scholar 

  45. Liu, Y.: Circuit implementation and finite-time synchronization of the 4D Rabinovich hyperchaotic system. Nonlinear Dyn. 67, 89–96 (2012)

  46. Liu, Y.: Hyperchaotic system from controlled Rabinovich system. Control Theor. Appl. 28, 1671–1678 (2011)

    Google Scholar 

  47. Kayode, O., Samuel, T.O.: Synchronization of 4D Rabinovich hyperchaotic systems for secure communication. J. Niger. Assoc. Math. Phys. 21, 35–40 (2012)

    Google Scholar 

  48. Sprott, J.C.: A proposed standard for the publication of new chaotic systems. Int. J. Bifurc. Chaos 21, 2391–2394 (2011)

    Article  MathSciNet  Google Scholar 

  49. Wolf, A., Swift, J.B., Swinney, H.L., Vastano, J.A.: Determining Lyapunov exponents from a time series. Phys. D 16, 285–317 (1985)

    Article  MATH  MathSciNet  Google Scholar 

  50. Leonov, G.A., Kuznetsov, N.V.: Time-varying linearization and the Perron effects. Int. J. Bifurc. Chaos 17, 1079–1107 (2007)

    Article  MATH  MathSciNet  Google Scholar 

  51. Kaplan, J., Yorke, J.: Lecture Notes in Mathematics, p. 204. Springer, Berlin (1979)

    Google Scholar 

  52. Hou, Z., Kang, N., Kong, X., Chen, G., Yan, G.: On the nonequivalence of Lorenz system and Chen system. Int. J. Bifurc. Chaos 20, 557–560 (2010)

    Article  MATH  MathSciNet  Google Scholar 

Download references

Acknowledgments

The authors acknowledge the referees and the editor for carefully reading this manuscript and suggesting many helpful comments. This work was supported by the Natural Science Foundation of China (11401543, 11290152, 11072008, 41230637), the Natural Science Foundation of Hubei Province (No. 2014CFB897), the Fundamental Research Funds for the Central Universities, China University of Geosciences (Wuhan) (No. CUGL150419), China Postdoctoral Science Foundation funded project (No. 2014M560028), Beijing Postdoctoral Research Foundation (2015ZZ), the Natural Science and Engineering Research Council of Canada (No. R2686A02) and the Funding Project for Academic Human Resources Development in Institutions of Higher Learning under the Jurisdiction of Beijing Municipality (PHRIHLB).

Author information

Authors and Affiliations

  1. School of Mathematics and Physics, China University of Geosciences, Wuhan, 430074, People’s Republic of China

    Zhouchao Wei

  2. College of Mechanical Engineering, Beijing University of Technology, Beijing, 100124, People’s Republic of China

    Zhouchao Wei, Wei Zhang & Minghui Yao

  3. Department of Applied Mathematics, Western University, London, ON, N6A 5B7, Canada

    Pei Yu

Authors
  1. Zhouchao Wei
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Pei Yu
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Wei Zhang
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Minghui Yao
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Wei Zhang.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Wei, Z., Yu, P., Zhang, W. et al. Study of hidden attractors, multiple limit cycles from Hopf bifurcation and boundedness of motion in the generalized hyperchaotic Rabinovich system. Nonlinear Dyn 82, 131–141 (2015). https://doi.org/10.1007/s11071-015-2144-8

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11071-015-2144-8

Keywords

Search

Navigation