Skip to main content
SpringerLink
Log in

A modified nonlinear POD method for order reduction based on transient time series

  • Original Paper
  • Published:
Nonlinear Dynamics Aims and scope Submit manuscript

Abstract

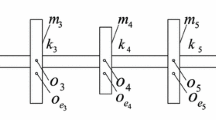
In this paper, a modified nonlinear proper orthogonal decomposition (POD) method based on transient time series on account of approximate inertial manifold method is proposed to reduce the order of the multiple degrees of freedom (DOFs) of a rotor system. A model of 23 DOFs rotor system comprising a pair of liquid-film bearing with pedestal looseness at one end is established by using the Newton’s second law. The multi-DOFs system is reduced to a two-DOFs model by using the modified POD method, which preserves the original dynamics behaviors. The comparison between the modified and the traditional POD method shows that the modified POD method is more effective especially in finding the bifurcation point and detecting the bifurcation diagrams and the mean square error of amplitudes curves. Finally, a relative error analysis is also carried out to evaluate the accuracy of the proposed order reduction method, indicating that the relative error is below 5 % excluding the interval between original bifurcation point and the shift of the reduced system.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5

Similar content being viewed by others

References

  1. Rega, G., Troger, H.: Dimension reduction of dynamical systems: methods, models, applications. Nonlinear Dyn. 41, 1–15 (2005)

    Article  MathSciNet  MATH  Google Scholar 

  2. Steindl, A., Troger, H.: Methods for dimension reduction and their application in nonlinear dynamics. Int. J. Solids Struct. 38, 2131–2147 (2001)

    Article  MATH  Google Scholar 

  3. Knobloch, E., Wiesenfeld, K.A.: Bifurcation in fluctuating systems: the centre manifold approach. J. Stat. Phys. 33, 611–637 (1983)

    Article  MathSciNet  MATH  Google Scholar 

  4. Verdugo, A., Rand, R.: Center manifold analysis of a DDE model of gene expression. Commun. Nonlinear Sci. Numer. Simul. 13, 1112–1120 (2008)

  5. Sinou, J.J., Thouverez, F., Jezequel, L.: Centre manifold and multivariable approximants applied to non-linear stability analysis. Int. J. Non-Linear Mech. 38, 1421–1442 (2003)

    Article  MATH  Google Scholar 

  6. Sun, C.J., Lin, Y.P., Han, M.A.: Stability and Hopf bifurcation for an epidemic disease model with delay. Chaos Solitons Fractals 30, 204–216 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  7. Song, Y.L., Wei, J.J., Yuan, Y.: Bifurcation analysis on a survival red blood cells model. J. Math. Anal. Appl. 316, 459–471 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  8. Nikolic, M., Rajkovic, M.: Bifurcations in nonlinear models of fluid-conveying pipes supported at both ends. J. Fluids Struct. 22, 173–195 (2006)

    Article  Google Scholar 

  9. Nishida, T., Teramoto, Y., Yoshihara, H.: Hopf bifurcation in viscous incompressible flow down an inclined plane. J. Math. Fluid Mech. 7, 29–71 (2005)

  10. Gentile, G., Mastropietro, V., Procesi, M.: Periodic solutions for completely resonant nonlinear wave equations with Dirichlet boundary conditions. Commun. Math. Phys. 256, 437–490 (2005)

    Article  MathSciNet  MATH  Google Scholar 

  11. Sandfry, R.A., Hall, C.D.: Bifurcations of relative equilibria of an oblate gyrostat with a discrete damper. Nonlinear Dyn. 48(3), 319–329 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  12. Edriss, S.: On approximate inertial manifolds to the Navier–Stokes equations. J. Math. Anal. Appl. 149, 540–557 (1990)

  13. Constantin, P., Foias, C.: Global Lyapunove exponents, Kaplan–Yorke formulas and the dimension of the attractors for 2D Navier–Stokes equations. Commun. Pure Appl. Math. 38, 1–27 (1985)

    Article  MathSciNet  MATH  Google Scholar 

  14. Constantin, P., Foias, C., Teman, R.: Attractors representing turbulent flows. Mem. Am. Math. Soc. 53, 1–65 (1985)

  15. Foias, C., Teman, R.: Some analytic and geometric properties of the solutions of the Navier–Stokes equations. J. Math. Pures Appl. 58, 339–368 (1979)

    MathSciNet  MATH  Google Scholar 

  16. Foial, C., Sell, G., Teman, R.: Inertial manifolds for nonlinear evolutionary equations. J. Differ. Equ. 73, 93–114 (1988)

  17. Marion, M.: Approximate inertial manifolds for reaction–diffusion equations in high space dimension. Dyn. Differ. Equ. 1, 245–267 (1989)

  18. Marion, M.: Approximate inertial manifolds for the Cahn–Hilliard equation. RAIRO Math. Model. Anal. Numer. 23, 463–488 (1989)

  19. Yang, H.L., Radons, G.: Geometry of inertial manifolds probed via a Lyapunov projection method. Phys. Rev. Lett. 108, 154101 (2012)

  20. Marion, M., Temam, R.: Nonlinear Galerkin methods. SIAM J. Numer Anal. 5, 1139–1157 (1989)

    Article  MathSciNet  Google Scholar 

  21. Glosmann, P., Kreuzer, E.: Nonlinear system analysis with Karhunen–Loeve transform. Nonlinear Dyn. 41, 111–128 (2005)

    Article  MathSciNet  Google Scholar 

  22. Georgiou, I.T.: Invariant manifolds, nonclassical normal modes, and proper orthogonal modes in the dynamics of the flexible spherical pendulum. Nonlinear Dyn. 25, 3–31 (2001)

    Article  MathSciNet  MATH  Google Scholar 

  23. Feldmann, U., Kreuzer, E., Pinto, F.: Dynamic diagnosis of railway tracks by means of Karhunen–Loeve transformation. Nonlinear Dyn. 22(2), 193–203 (2000)

    Article  MATH  Google Scholar 

  24. Kerschen, G., Golinval, J.C., Vakakis, A.F., Bergman, L.A.: The method of proper orthogonal decomposition for dynamical characterization and order reduction of mechanical systems: an overview. Nonlinear Dyn. 41, 147–169 (2005)

  25. Kappagantu, R., Feeny, B.F.: Part 1: dynamical characterization of a frictionally exited beam. Nonlinear Dyn. 22(4), 317–333 (2000)

    Article  MATH  Google Scholar 

  26. Kappagantu, R., Feeny, B.F.: Part 2: proper orthogonal modal modeling of a frictionally excited beam. Nonlinear Dyn. 23, 1–11 (2000)

    Article  MATH  Google Scholar 

  27. Amabili, M., Touze, C.: Reduced-order models for nonlinear vibrations of fluid-filled circular cylindrical shells: comparison of POD and asymptotic nonlinear normal modes methods. J. Fluids Struct. 23(6), 885–903 (2007)

    Article  Google Scholar 

  28. Liang, Y.C., Lee, H.P., Lim, S.P., Lin, W.Z., Lee, K.H., Wu, C.G.: Proper orthogonal decomposition and its applications, part I: theory. J. Sound Vib. 252(3), 527–544 (2002)

    Article  MathSciNet  MATH  Google Scholar 

  29. Liang, Y.C., Lin, W.Z., Lee, H.P., Lim, S.P., Lee, K.H., Sun, H.: Proper orthogonal decomposition and its applications, part II: model reduction for MEMS dynamical analysis. J. Sound Vib. 256(3), 515–532 (2002)

    Article  Google Scholar 

  30. Terragni, F., Jose, M.V.: On the use of POD-based ROMs to analyze bifurcations in some dissipative systems. Phys. D 241, 1393–1405 (2012)

  31. Couplet, M., Basdevant, C., Sagaut, P.: Calibrated reduced-order POD-Galerkin system for fluid flow modeling. J. Comput. Phys. 207, 192–220 (2005)

    Article  MathSciNet  MATH  Google Scholar 

  32. Sirisup, S., Karniadakis, G.E., Kevrekidis, I.G.: Equations-free/Galerkin-free POD assisted computation of incompressible flows. J. Comput. Phys. 207, 568–587 (2005)

    Article  MathSciNet  MATH  Google Scholar 

  33. Rapun, M.L., Vega, J.M.: Reduced order models based on local POD plus Galerkin projection. J. Comput. Phys. 229, 3046–3063 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  34. Terragni, F., Valero, E., Vega, J.M.: Local POD plus Galerkin projection in the unsteady lid-driven cavity problem. SIAM J. Sci. Comput. 33, 3538–3561 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  35. Nayfeh, A.H., Balachandran, B.: Applied Nonlinear Dynamics: Analytical, Computational and Experimental Methods. Wiley, New York (1995)

    Book  MATH  Google Scholar 

  36. Chen, Y.S., Leung, A.Y.T.: Bifurcation and Chaos in Engineering. Springer, London (1998)

    Book  MATH  Google Scholar 

  37. Yu, H., Chen, Y.S., Cao, Q.J.: Bifurcation analysis for nonlinear multi-degree-of-freedom rotor system with liquid-film lubricated bearings. Appl. Math. Mech. Engl. Ed. 34(6), 777–790 (2013)

    Article  Google Scholar 

  38. Teman, R.: Navier–Stokes Equations and Nonlinear Functional Analysis. SIAM, Philadelphia (1983)

    Google Scholar 

  39. Teman, R.: Navier–Stokes Equation, Theory and Numerical Analysis, 3rd edn. North-Holland, Amsterdam (1984)

    Google Scholar 

  40. Adiletta, G., Guido, A.R., Rossi, C.: Chaotic motions of a rigid rotor in short journal bearings. Nonlinear Dyn. 10, 251–269 (1996)

    Article  Google Scholar 

Download references

Acknowledgments

The authors would like to acknowledge the financial supports from the Natural Science Foundation of China (Grant Nos. 10632040 and 11372082).

Author information

Authors and Affiliations

  1. School of Astronautics, Harbin Institute of Technology, Harbin , 150001, People’s Republic of China

    Kuan Lu, Hai Yu, Yushu Chen, Qingjie Cao & Lei Hou

Authors
  1. Kuan Lu
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Hai Yu
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Yushu Chen
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Qingjie Cao
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Lei Hou
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Kuan Lu.

Appendix

Appendix

$$\begin{aligned} c_{11}&= 10^{-2}\left( 1.9979\frac{c_1 }{m_1 }+6.3193\frac{c_2 }{m_2 }+9.9517\frac{c_3 }{m_3 }\right. \\&\quad +\,12.954\frac{c_4 }{m_4 }+14.934\frac{c_5 }{m_5 }+14.896\frac{c_6 }{m_6 } \\&\quad +\,13.546\frac{c_7 }{m_7 }+11.033\frac{c_8 }{m_8 }+7.7582\frac{c_9 }{m_9 }\\&\quad \left. +\,4.4199\frac{c_{10} }{m_{10} }+2.0503\frac{c_{11} }{m_{11} }+0.14015\frac{c_s }{m_{12} }\right) \\ c_{12}&= 10^{-2}\left( 0.1747\frac{c_1 }{m_1 }+0.50805\frac{c_2 }{m_2 }+0.43517\frac{c_3 }{m_3 }\right. \\&\quad +\,0.21398\frac{c_4 }{m_4 }-0.05375\frac{c_5 }{m_5 }-0.26634\frac{c_6 }{m_6 } \\&\quad -\,0.35194\frac{c_7 }{m_7 }-0.31994\frac{c_8 }{m_8 }-0.21875\frac{c_9 }{m_9 }\\&\quad \left. -\,0.11377\frac{c_{10} }{m_{10} }\!-\!0.1043\frac{c_{11} }{m_{11} }\!+\!0.096872\frac{c_s }{m_{12} }\right) \\ c_{21}&= 10^{-2}(0.1747\frac{c_1 }{m_1 }+0.50805\frac{c_2 }{m_2 }+0.43517\frac{c_3 }{m_3 }\\&\quad +\,0.21398\frac{c_4 }{m_4 }-0.05375\frac{c_5 }{m_5 }-0.26634\frac{c_6 }{m_6 } \\&\quad -\,0.35194\frac{c_7 }{m_7 }-0.31994\frac{c_8 }{m_8 }-0.21875\frac{c_9 }{m_9 }\\&\quad -\,0.11377\frac{c_{10} }{m_{10} }-0.1043\frac{c_{11} }{m_{11} }+0.096872\frac{c_s }{m_{12} }) \\ c_{22}&= 10^{-2}\left( 3.9645\frac{c_1 }{m_1 }+7.7322\frac{c_2 }{m_2 }+10.581\frac{c_3 }{m_3 }\right. \\&\quad +\,12.825\frac{c_4 }{m_4 }+14.171\frac{c_5 }{m_5 }+13.867\frac{c_6 }{m_6 } \\&\quad +\,12.461\frac{c_7 }{m_7 }+10.136\frac{c_8 }{m_8 }+7.2763\frac{c_9 }{m_9 }\\&\quad \left. +\,4.4643\frac{c_{10} }{m_{10} }+2.455\frac{c_{11} }{m_{11} }+0.0066975\frac{c_s }{m_{12} }\right) \end{aligned}$$
$$\begin{aligned} k_{11}&= 10^{-8}\left( -0.03547\frac{k_5 }{m_6 }+1.3019\frac{k_6 }{m_6 }+0.263\frac{k_s }{m_{12} }\right. \\&\quad -\,2.7589\frac{k_8 }{m_9 }+3.6742\frac{k_9 }{m_9 }+5.3886\frac{k_1 }{m_2 }\\&\quad -\,2.9737\frac{k_2 }{m_2 }+3.0203\frac{k_3 }{m_4 } \\&\quad -\,1.7859\frac{k_4 }{m_4 }+1.928\frac{k_4 }{m_5 }+0.035518\frac{k_5 }{m_5 }\\&\quad -\,1.5408\frac{k_{10} }{m_{11} }-1.2315\frac{k_6 }{m_7 }+2.4972\frac{k_7 }{m_7 }\\&\quad +\,3.8427\frac{k_2 }{m_3 }-2.6143\frac{k_3 }{m_3 } \\&\quad +\,2.5903\frac{k_9 }{m_{10} }+2.9058\frac{k_{10} }{m_{10} }-2.2172\frac{k_7 }{m_8 }\\&\quad \left. -\,2.7206\frac{k_1 }{m_1 }+3.3869\frac{k_8 }{m_8 }\right) \\ k_{12}&= 10^{-8}\left( -0.40584\frac{k_5 }{m_6 }-0.30843\frac{k_6 }{m_6 }\right. \\&\quad +\,0.18178\frac{k_s }{m_{12} }\\&\quad +\,1.277\frac{k_8 }{m_9 }-1.6474\frac{k_9 }{m_9 }-1.8797\frac{k_1 }{m_2 }\\&\quad +\,1.5507\frac{k_2 }{m_2 }-1.4206\frac{k_3 }{m_4 } \\&\quad +\,0.99842\frac{k_4 }{m_4 }-1.0456\frac{k_4 }{m_5 }+0.40628\frac{k_5 }{m_5 }\\&\quad +\,1.6473\frac{k_{10} }{m_{11} }+0.32023\frac{k_6 }{m_7 }-0.89506\frac{k_7 }{m_7 }\\&\quad -\,1.7101\frac{k_2 }{m_3 }+1.3256\frac{k_3 }{m_3 } \\&\quad +\,1.5552\frac{k_9 }{m_{10} }-1.7937\frac{k_{10} }{m_{10} }+0.89517\frac{k_7 }{m_8 }\\&\quad \left. +\,1.5869\frac{k_1 }{m_1 }-1.3098\frac{k_8 }{m_8 }\right) \end{aligned}$$
$$\begin{aligned} k_{21}&= 10^{-8}\left( -0.0073538\frac{k_5 }{m_6 }+0.48086\frac{k_6 }{m_6 }\right. \\&\quad +\,0.18178\frac{k_s }{m_{12} }-\,1.1199\frac{k_8 }{m_9 }+1.3582\frac{k_9 }{m_9 }\\&\quad +2.2124\frac{k_1 }{m_2 }-\,1.5733\frac{k_2 }{m_2 }+0.91057\frac{k_3 }{m_4 } \\&\quad -\,0.54315\frac{k_4 }{m_4 }+0.49602\frac{k_4 }{m_5 }-0.0069134\frac{k_5 }{m_5 }\\&\quad -\,1.7759\frac{k_{10} }{m_{11} }-0.46906\frac{k_6 }{m_7 }+0.83512\frac{k_7 }{m_7 }\\&\quad +\,1.4139\frac{k_2 }{m_3 }+1.0056\frac{k_3 }{m_3 } \\&\quad -\,1.4504\frac{k_9 }{m_{10} }+1.6295\frac{k_{10} }{m_{10} }-0.83501\frac{k_7 }{m_8 }\\&\quad \left. -\,2.5053\frac{k_1 }{m_1 }+1.0871\frac{k_8 }{m_8 }\right) \\ k_{22}&= 10^{-8}\left( -2.8136\frac{k_5 }{m_6 }\!+\!1.3556\frac{k_6 }{m_6 }\!+\!0.12565\frac{k_s }{m_{12} }\right. \\&\quad -\,2.4191\frac{k_8 }{m_9 }+3.0657\frac{k_9 }{m_9 }+4.4024\frac{k_1 }{m_2 }\\&\quad -\,2.3578\frac{k_2 }{m_2 }+2.255\frac{k_3 }{m_4 } \\&\quad -\,1.2115\frac{k_4 }{m_4 }+0.29045\frac{k_4 }{m_5 }-1.3564\frac{k_5 }{m_5 }\\&\quad -\,1.2821\frac{k_{10} }{m_{11} }\\&\quad +\,2.309\frac{k_6 }{m_7 }+2.9876\frac{k_7 }{m_7 }-1.9562\frac{k_2 }{m_3 }\\&\quad -\,2.2111\frac{k_3 }{m_3 } \\&\quad +\,2.414\frac{k_9 }{m_{10} }-2.0539\frac{k_{10} }{m_{10} }-2.0539\frac{k_7 }{m_8 }\\&\quad \left. -\,2.6678\frac{k_1 }{m_1 }+2.9474\frac{k_8 }{m_8 }\right) \end{aligned}$$
$$\begin{aligned} f_1&= -\frac{0.13413}{M_1 }f_{1x} -\frac{0.044593}{M_1 }f_{1y} -\frac{0.12501}{M_{11} }f_{2x} \\&\quad -\,\frac{0.069826}{M_{11} }f_{2y} -\frac{0.037437}{M_{12} }f_{1y}\\ f_{1x}&= f_x (-0.31552p_1 -0.012433p_2 , 0.001973p_1\\&\quad +\,0.34105p_2 \\&\quad -\,0.34855\dot{p}_1 +0.011375\dot{p}_2 , 0.014298\dot{p}_1\\&\quad +\,0.35867\dot{p}_2 ) \\ f_{1y}&= f_y (-0.31546p_1 -0.012273p_2 , 0.001477p_1\\&\quad +\,0.32505p_2 \\&\quad -\,0.35955\dot{p}_1 +0.010275\dot{p}_2 , 0.016298\dot{p}_1\\&\quad +\,0.35797\dot{p}_2 ) \\ f_{\omega 1}&= -0.25064b_2 \cos t-0.31546b_3 \cos t\\&\quad -\,0.35955b_4 \cos t-0.38562b_5 \cos t\\&\quad -\,0.38513b_6 \cos t-0.36766b_7 \cos t \\&\quad -\,0.33216b_8 \cos t-0.27792b_9 \cos t\\&\quad -\,0.20586b_{10} \cos t+0.001592b_8 \sin t\\&\quad +\,0.016822b_7 \sin t+0.016298b_4 \sin t \\&\quad -\,0.018518b_9 \sin t+0.025132b_5 \sin t\\&\quad +\,0.025196b_6 \sin t-0.019256b_2 \sin t\\&\quad +\,0.001477b_3 \sin t-0.042671b_{10} \sin t \end{aligned}$$
$$\begin{aligned} f_2&= -\frac{0.074424}{M_1 }f_{1x} +\frac{0.18468}{M_1 }f_{1y} -\frac{0.069966}{M_{11} }f_{2x} \\&\quad +\,\frac{0.1402}{M_{11} }f_{2y} -\frac{0.025876}{M_{12} }f_{1y}\\ \end{aligned}$$
$$\begin{aligned} f_{2x}&= f_x (-0.38562p_1 +0.02587p_2 , 0.025132p_1\\&\quad +\,0.37556p_2 \\&\quad -\,0.38513\dot{p}_1 +0.031192\dot{p}_2 , 0.025196\dot{p}_1\\&\quad +\,0.37107\dot{p}_2 ) \\ f_{2y}&= f_y (-0.36766p_1 +0.02568p_2 , 0.016822p_1\\&\quad +\,0.35207p_2 \\&\quad -\,0.33216\dot{p}_1 +0.011157\dot{p}_2 , 0.001592\dot{p}_1\\&\quad +\,0.31818\dot{p}_2 ) \end{aligned}$$
$$\begin{aligned} f_{\omega 2}&= -0.041395b_2 \cos t-0.012273b_3 \cos t\\&\quad +\,0.010275b_4 \cos t+0.02587b_5 \cos t\\&\quad +\,0.031192b_6 \cos t+0.025681b_7 \cos t \\&\quad +\,0.01157b_8 \cos t-0.01009b_9 \cos t\\&\quad -\,0.037572b_{10} \cos t+0.31818b_8 \sin t\\&\quad +\,0.35207b_7 \sin t+0.35797b_4 \sin t \\&\quad +\,0.26956b_9 \sin t+0.37556b_5 \sin t\\&\quad +\,0.27497b_6 \sin t+0.32505b_2 \sin t\\&\quad +\,0.001477b_3 \sin t+0.20792b_{10} \sin t \\ g_1&= 0.07091G, g_2 =3.2031G \end{aligned}$$

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Lu, K., Yu, H., Chen, Y. et al. A modified nonlinear POD method for order reduction based on transient time series. Nonlinear Dyn 79, 1195–1206 (2015). https://doi.org/10.1007/s11071-014-1736-z

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11071-014-1736-z

Keywords

Search

Navigation