Skip to main content
SpringerLink
Log in

Multi-soliton solutions for the three-coupled KdV equations engendered by the Neumann system

  • Original Paper
  • Published:
Nonlinear Dynamics Aims and scope Submit manuscript

Abstract

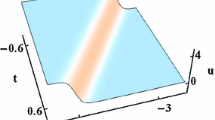
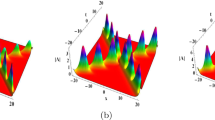
Korteweg–de Vries (KdV)-type equations describe certain nonlinear phenomena in fluids and plasmas. In this paper, three-coupled KdV equations corresponding to the Neumann system of the fourth-order eigenvalue problem is investigated. Through the dependent variable transformations, bilinear forms of such equations are obtained, from which the multi-soliton solutions are derived. Soliton propagation and interaction are analyzed: (1) Bell- and anti-bell-shaped solitons are found; (2) Among the soliton images, one depends on the sign of wave numbers k i ’s (i=1,2,3), while the others are independent of such a sign; (3) Interaction between two solitons and among three solitons are elastic, i.e., the amplitude and velocity of each soliton remain unvaried after the interaction except for the phase shift.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8

Similar content being viewed by others

References

  1. Tian, B., Gao, Y.T.: Spherical nebulons and Bäcklund plasma with symbolic computation. Eur. Phys. J. D 33, 59–65 (2005)

    Article  Google Scholar 

  2. Yan, Z.Y., Zhang, H.Q.: Symbolic computation and new families of exact soliton-like solutions to the integrable Broer–Kaup (BK) equations in (2+1)-dimensional spaces. J. Phys. A 34, 1785–1793 (2001)

    Article  MATH  MathSciNet  Google Scholar 

  3. Gao, Y.T., Tian, B.: Cosmic dust-ion-acoustic waves, spherical modified Kadomtsev–Petviashvili model, and symbolic computation. Phys. Plasmas 13, 112901 (2006)

    Article  Google Scholar 

  4. Tian, B., Shan, W.R., Zhang, C.Y., Wei, G.M., Gao, Y.T.: Transformations for a generalized variable-coefficient nonlinear Schördinger model from plasma physics, arterial mechanics and optical fibers with symbolic computation. Eur. Phys. J. B 47, 329–332 (2005)

    Article  Google Scholar 

  5. Barnett, M.P., Capitani, J.F., Gathen, V.Z., Gerhard, J.: Symbolic calculation in chemistry, selected examples. Int. J. Quant. Chem. 100, 80–104 (2004)

    Article  Google Scholar 

  6. Ablowitz, M.J., Segur, H.: Solitons and the Inverse Scattering Transform. SIAM, Philadelphia (1981)

    Book  MATH  Google Scholar 

  7. Ablowitz, M.J., Clarkson, P.A.: Solitons, Nonlinear Evolution Equation and Inverse Scattering. Cambridge Univ. Press, New York (1991)

    Book  Google Scholar 

  8. Biswas, A., Ismail, M.S.: 1-Soliton solution of the coupled KdV equation and Gear Grimshaw model. Appl. Math. Comput. 216, 3662–3670 (2010)

    Article  MATH  MathSciNet  Google Scholar 

  9. Wang, D.S.: Integrability of a coupled KdV system: Painlevé property Lax pair and Bäcklund transformation. Appl. Math. Comput. 216, 1349–1354 (2010)

    Article  MATH  MathSciNet  Google Scholar 

  10. Svinolupov, S.I.: Jordan algebras and generalized KdV equations. Theor. Mat. Fiz. 87, 391–403 (1991)

    MathSciNet  Google Scholar 

  11. Svinolupov, S.I.: Jordan algebras and integrable systems. Funct. Anal. Appl. 27, 257–265 (1994)

    Article  MathSciNet  Google Scholar 

  12. Güses, M., Karasu, A.: Degenerate Svinolupov KdV systems. Phys. Lett. A 214, 21–26 (1996)

    Article  MathSciNet  Google Scholar 

  13. Karasu, A.: Jordan KdV systems and Painlevé property. Int. J. Theor. Phys. 36, 705–713 (1997)

    Article  MATH  MathSciNet  Google Scholar 

  14. Antonowicz, M., Fordy, A.P.: Coupled KdV equations with multi-Hamiltonian structures. J. Phys. D 28, 345–357 (1987)

    Article  MATH  MathSciNet  Google Scholar 

  15. Athorne, C., Fordy, A.P.: Generalized KdV and MKdV equations associated with symmetric spaces. J. Phys. A 20, 377–387 (1987)

    Article  MathSciNet  Google Scholar 

  16. Zhao, Y., Gu, Z.Q., Liu, Y.F.: The Neumann system for the 4th-order eigenvalue problem and constraint flows of the coupled KdV-type equations. Eur. Phys. J. Plus 127, 77–90 (2012)

    Article  Google Scholar 

  17. Neumann, C.: De problemate quodam mechanico, quod ad priman integralium ultraellipticorum classem revocatur. J. Reine Angew. Math. 56, 46–63 (1859)

    Article  MATH  Google Scholar 

  18. Lax, P.D.: Lectures in Appl. Math. Periodic solutions of the KdV equations lectures. Lect. Appl. Math. 15, 85–96 (1974)

    MathSciNet  Google Scholar 

  19. Novikov, S.P.: Funkts: periodic problem for the Korteweg–de Vries equation. Anal. Prilozh. 8, 54–66 (1974)

    Google Scholar 

  20. Flaschka, H., McLaughlin, D.W.: Prog. Theor. Phys. 55, 438–456 (1976)

    Article  MATH  MathSciNet  Google Scholar 

  21. Alber, S.I.: Investigation of equations of Korteweg–de Vries type by the method of recurrence relations. J. Lond. Math. Soc. 19, 467–480 (1979)

    Article  MathSciNet  Google Scholar 

  22. Gu, Z.Q.: The Neumann system for the 3rd-order eigenvalue problems related to the Boussinesq equation. Nuovo Cimento B 117, 615–632 (2002)

    Google Scholar 

  23. Hirota, R.: The Direct Method in Soliton Theory. Cambridge Univ. Press, Cambridge (2004)

    Book  MATH  Google Scholar 

  24. Flaschka, H.: Symposium on Non-linear Integrable Systems Classical Theory and Quantum Theory. World Sci., Kyoto (1981)

    Google Scholar 

  25. Whitham, G.B.: Linear and Nonlinear Waves. Wiley, New York (1974)

    MATH  Google Scholar 

  26. Johnson, R.S.: A Modern Introduction to the Mathematical Theory of Water Waves. Cambridge Univ. Press, Cambridge (1997)

    Book  MATH  Google Scholar 

  27. Daripa, P.: Higher-order Boussinesq equations for two-way propagation of shallow water waves. Eur. J. Mech. B, Fluids 25, 1008–1021 (2006)

    Article  MATH  MathSciNet  Google Scholar 

  28. Szilagyi, J., Parlange, M.B.: Baseflow separation based on analytical solutions of the Boussinesq equation. J. Hydrol. 204, 251–260 (1998)

    Article  Google Scholar 

  29. Gu, Z.Q.: Complex confocal involutive system associated with the solution of the AKNS evolution equation. J. Math. Phys. 32, 1498–1504 (1991)

    Article  MATH  MathSciNet  Google Scholar 

  30. Lax, P.D.: Integrals of nonlinear equations of evolution and solitary waves. Commun. Pure Appl. Math. 21, 467–490 (1968)

    Article  MATH  MathSciNet  Google Scholar 

  31. Sawada, K., Kotera, T.: Prog. Theor. Phys. 51, 1355 (1974)

    Article  MATH  MathSciNet  Google Scholar 

  32. Caudrey, P.J., Dodd, R.K., Gibbon, J.D.: A new hierarchy of Korteweg–de Vries equations. Proc. R. Soc. Lond. Ser. A, Math. Phys. Sci. 351, 407–422 (1976)

    Article  MATH  MathSciNet  Google Scholar 

  33. Kaup, D.J.: On the inverse scattering problem for cubic eigenvalue problems of the class ϕ xxx +6Qϕ x +6Rϕ=λϕ. Stud. Appl. Math. 62, 189–216 (1980)

    MATH  MathSciNet  Google Scholar 

  34. Kupershmidt, B.A.: Phys. Lett. A 102, 213 (1984)

    Article  MathSciNet  Google Scholar 

  35. Chen, J.B.: A class of Neumann type systems and its application. Dyn. Partial Differ. Equ. 9, 147–171 (2012)

    Article  MATH  MathSciNet  Google Scholar 

  36. Benes, N., Kasman, A., Young, K.: On decompositions of the KdV 2-soliton. J. Nonlinear Sci. 16, 179–200 (2006)

    Article  MATH  MathSciNet  Google Scholar 

  37. Christov, I., Christov, C.I.: Mechanics research communications. Phys. Lett. A 372, 481–486 (2008)

    Article  Google Scholar 

  38. Hirota, R.: Extact solution of the KdV equation for multiple collisions of soliton. Phys. Rev. Lett. 27, 1184–1192 (1971)

    Article  Google Scholar 

  39. Satsuma, J.: J. Phys. Soc. Jpn. 40, 286 (1976)

    Article  MathSciNet  Google Scholar 

  40. Satsuma, J., Kaup, D.J.: J. Phys. Soc. Jpn. 43, 692 (1977)

    Article  MathSciNet  Google Scholar 

  41. Matveev, V.B., Salle, M.A.: Darboux Transformations and Solitons. Springer, New York (1991)

    Book  MATH  Google Scholar 

  42. Tian, B., Gao, Y.T.: Spherical Kadomtsev–Petviashvili equation and nebulons for dust ion-acoustic waves with symbolic computation. Phys. Lett. A 340, 243–250 (2005)

    Article  MATH  Google Scholar 

  43. Xu, T., Tian, B., Li, L.L., Lü, X., Zhang, C.: Dynamics of Alfvén solitons in inhomogeneous plasmas. Phys. Plasmas 15, 102307 (2008)

    Article  Google Scholar 

  44. Zhang, Y., Song, Y., Cheng, L., Ge, J.Y., Wei, W.W.: Exact solutions and Painlevé analysis of a new (2+1)-dimensional generalized KdV equation. Nonlinear Dyn. 68, 445–458 (2012)

    Article  MATH  MathSciNet  Google Scholar 

  45. Lü, X.: Novel behavior and properties forthe nonlinear pulse propagation in optical fibers. Europhys. Lett. 97, 10005 (2012)

    Article  Google Scholar 

  46. Lü, X.: Vector bright soliton behaviors associated with negative coherent coupling. Phys. Rev. E 85, 026117 (2012)

    Article  Google Scholar 

  47. Lü, X.: Soliton solutions via auxiliary function method for a coherently-coupled model in the optical fiber communications. Nonl. Anal., Real World Appl. 14, 929–939 (2013)

    Article  MATH  Google Scholar 

  48. Jiang, Y., Tian, B., Liu, W.J., Sun, K., Li, M., Wang, P.: Soliton interactions and complexes for coupled nonlinear Schrodinger equations. Phys. Rev. E 85, 036605 (2012)

    Article  Google Scholar 

  49. Jiang, Y., Tian, B., Liu, W.J., Li, M., Wang, P., Sun, K.: Solitons, Backlund transformation, and Lax pair for the (2+1)-dimensional Boiti-Leon-Pempinelli equation for the water waves. J. Math. Phys. 51, 093519 (2010)

    Article  MathSciNet  Google Scholar 

  50. Wang, P., Tian, B., Liu, W.J., Li, M., Sun, K.: Soliton solutions for a generalized inhomogeneous variable-coefficient Hirota equation with symbolic computation. Stud. Appl. Math. 125, 213–222 (2010)

    MATH  MathSciNet  Google Scholar 

  51. Wang, P., Tian, B., Liu, W.J., Qu, Q.X., Li, M., Sun, K.: Lax pair, conservation laws and N-soliton solutions for the extended Korteweg-de Vries equations in fluids. Eur. Phys. J. D 61, 701–708 (2011)

    Article  Google Scholar 

Download references

Acknowledgements

We express our sincere thanks to all the members of our discussion group for their valuable comments. This work has been supported by the National Natural Science Foundation of China under Grant No. 11272023, and by the Open Fund of State Key Laboratory of Information Photonics and Optical Communications (Beijing University of Posts and Telecommunications).

Author information

Authors and Affiliations

  1. Ministry-of-Education Key Laboratory of Fluid Mechanics and National Laboratory for Computational Fluid Dynamics, Beijing University of Aeronautics and Astronautics, Beijing, 100191, China

    Da-Wei Zuo, Yi-Tian Gao, Gao-Qing Meng, Yu-Jia Shen & Xin Yu

  2. Department of Mathematics and Physics, Shijiazhuang Tiedao University, Shijiazhuang, 050043, China

    Da-Wei Zuo

Authors
  1. Da-Wei Zuo
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Yi-Tian Gao
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Gao-Qing Meng
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Yu-Jia Shen
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Xin Yu
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Yi-Tian Gao.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Zuo, DW., Gao, YT., Meng, GQ. et al. Multi-soliton solutions for the three-coupled KdV equations engendered by the Neumann system. Nonlinear Dyn 75, 701–708 (2014). https://doi.org/10.1007/s11071-013-1096-0

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11071-013-1096-0

Keywords

Search

Navigation