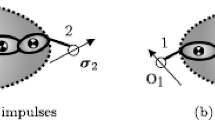Skip to main content
SpringerLink
Log in

Orthogonal Complement Based Divide-and-Conquer Algorithm for constrained multibody systems

  • Original Article
  • Published:
Nonlinear Dynamics Aims and scope Submit manuscript

Abstract

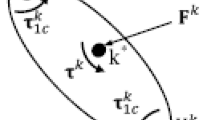
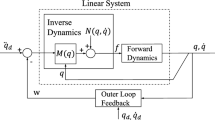
A new algorithm, Orthogonal Complement based Divide-and-Conquer Algorithm (O-DCA), is presented in this paper for calculating the forward dynamics of constrained multi-rigid bodies including topologies involving single or coupled closed kinematic loops. The algorithm is exact and noniterative. The constraints are imposed at the acceleration level by utilizing a kinematic relation between the joint motion subspace (or partial velocities) and its orthogonal complement. Sample test cases indicate excellent constraint satisfaction and robust handling of singular configurations. Since the present algorithm does not use either a reduction or augmentation approach in the traditional sense for imposing the constraints, it does not suffer from the associated problems for systems passing through singular configurations. The computational complexity of the algorithm is expected to be O(n+m) and O(log(n+m)) for serial and parallel implementation, respectively, where n is the number of generalized coordinates and m is the number of independent algebraic constraints.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Hooker, W.W., Margulies, G.: The dynamical attitude equations for an n-body satellite. J. Astronaut. Sci. 7(4), 123–128 (1965)

    MathSciNet  Google Scholar 

  2. Luh, J.S.Y., Walker, M.W., Paul, R.P.C.: On-line computational scheme for mechanical manipulators. J. Dynam. Syst. Meas. Control 102, 69–76 (1980)

    MathSciNet  Google Scholar 

  3. Walker, M.W., Orin, D.E.: Efficient dynamic computer simulation of robotic mechanisms. J. Dynam. Syst. Meas. Control 104, 205–211 (1982)

    MATH  Google Scholar 

  4. Rosenthal, D.E., Sherman, M.A.: High performance multibody simulations via symbolic equation manipulation and Kane's method. J. Astronaut. Sci. 34(3), 223–239 (1986)

    Google Scholar 

  5. Neilan, P.E.: Efficient computer simulation of motions of multibody systems. PhD Thesis, Stanford University (1986)

  6. Vereshchagin, A.F.: Computer simulation of the dynamics of complicated mechanisms of robot-manipulators. Eng. Cybernet. 12(6), 65–70 (1974)

    Google Scholar 

  7. Armstrong, W.W.: Recursive solution to the equations of motion of an n-link manipulator. In: Fifth World Congress on the Theory of Machines and Mechanisms, Vol. 2, Montreal, Canada, pp 1342–1346 (1979)

  8. Featherstone, R.: The calculation of robotic dynamics using articulated body inertias. Int. J. Rob. Res. 2(1), 13–30 (1983)

    Google Scholar 

  9. Brandl, H., Johanni, R., Otter, M.: A very efficient algorithm for the simulation of robots and similar multibody systems without inversion of the mass matrix. In: IFAC/IFIP/IMACS Symposium, Vienna, Austria (1986)

  10. Bae, D.S., Haug, E.J.: A recursive formation for constrained mechanical system dynamics: Part I, Open loop systems. Mech. Struct. Machines 15(3), 359–382 (1987)

    Google Scholar 

  11. Rosenthal, D.E.: An order n formulation for robotic systems. J. Astronaut. Sci. 38(4), 511–529 (1990)

    Google Scholar 

  12. Anderson, K.S.: Recursive derivation of explicit equations of motion for efficient dynamic/control simulation of large multibody systems. PhD Thesis, Stanford University, Stanford, CA(1990)

  13. Kreutz-Delgado, K., Jain, A., Rodriguez, G.: Recursive formulation of operational space control. Int. J. Rob. Res. 11(4), 320–328 (1992)

    Google Scholar 

  14. Jain, A.: Unified formulation of dynamics for serial rigid multibody systems. J. Guid. Control Dynam. 14(3), 531–542 (1991)

    MATH  Google Scholar 

  15. Featherstone, R.: Robot Dynamics Algorithms. Kluwer Academic, New York (1987)

    Google Scholar 

  16. Bae, D.S., Haug, E.J.: A recursive formation for constrained mechanical system dynamics: Part II, Closed loop systems. Mech. Struct. Machines 15(4), 481–506 (1987)

    Google Scholar 

  17. Wehage, R.A.: Application of matrix partitioning and recursive projection to O(n) solution of constrained equations of motion. In: ASME Design Engineering Division, DE, Vol. 15-2, pp. 221–230 (1988)

  18. Anderson, K.S., Critchley, J.H.: Improved order-n performance algorithm for the simulation of constrained multi-rigid-body systems. Multibody Syst. Dynam. 9, 185–212 (2003)

    Article  MathSciNet  MATH  Google Scholar 

  19. Critchley, J.H., Anderson, K.S.: A generalized recursive coordinate reduction method for multibody system dynamics. J. Multiscale Comput. Eng. 1(2 & 3), 181–200 (2003)

    Article  Google Scholar 

  20. Lötstedt, P.: On a penalty function method for the simulation of mechanical systems subject to constraints. Report TRITA-NA-7919, Royal Institute of Technology, Stockholm, Sweden (1979)

  21. Lötstedt, P.: Mechanical systems of rigid bodies subject to unilateral constraints. SIAM J. Appl. Math. 42(2), 281–296 (1982)

    Article  MathSciNet  MATH  Google Scholar 

  22. Baumgarte, J.: Stabilization of constraints and integrals of motion in dynamic systems. Comput. Method Appl. Mech. Eng. 1, 1–16 (1972)

    Article  MathSciNet  MATH  Google Scholar 

  23. Baumgarte, J.W.: A new method for stabilization of holonomic contraints. J. Appl. Mech. 50, 869–870 (1983)

    Article  MathSciNet  MATH  Google Scholar 

  24. Park, K.C., Chiou, J.C.: Stabilization of computational procedures for constrained dynamical systems. J. Guid. Control Dynam. 11(4), 365–370 (1988)

    Article  MathSciNet  MATH  Google Scholar 

  25. Bayo, E., Garcia de Jalon, J., Serna, M.A.: Modified Lagrangian formulation for the dynamic analysis of constrained mechanical systems. Comput. Methods Appl. Mech. Eng. 71(2), 183–195 (1988)

    Article  MathSciNet  MATH  Google Scholar 

  26. Anderson, K.S.: An order-n formulation for motion simulation of general constrained multi-rigid-body systems. Comput. Struct. 43(3), 565–572 (1992)

    Article  MATH  Google Scholar 

  27. Stejskal, V., Valášek, M.: Kinematics and Dynamics of Machinery. Marcel Dekker, New York (1996)

    Google Scholar 

  28. Saha, S.K., Schiehlen, W.O.: Recursive kinematics and dynamics for parallel structured closed-loop multibody systems. Mech. Struct. Machines 29(2), 143–175 (2001)

    Article  Google Scholar 

  29. Fijany, A., Sharf, I., D'Eleuterio, G.M.T.: Parallel O(log n) algorithms for computation of manipulator forward dynamics. IEEE Trans. Rob. Autom. 11(3), 389–400 (1995)

    Article  Google Scholar 

  30. Featherstone, R.: A divide-and-conquer articulated body algorithm for parallel O(log(n)) calculation of rigid body dynamics. Part 1: Basic algorithm. Int. J. Rob. Res. 18(9), 867–875 (1999)

    Article  Google Scholar 

  31. Featherstone, R.: A divide-and-conquer articulated body algorithm for parallel O(log(n)) calculation of rigid body dynamics. Part 2: Trees, loops, and accuracy. Int. J. Rob. Res. 18(9), 876–892 (1999)

    Article  Google Scholar 

  32. Kim S.S., VanderPloeg M.J.: Generalized and efficient method for dynamic analysis of mechanical systems using velocity transforms. J. Mech. Trans. Autom. Des. 108(2), 1986, 176–182.

    Article  Google Scholar 

  33. Nikravesh P.E.: Systematic reduction of multibody equations to a minimal set. Int. J. Non-Linear Mech. 25(2–3), 143–151 (1990)

    Article  MATH  Google Scholar 

  34. Kane T.R., Levinson D.A.: Dynamics: Theory and Application. McGraw-Hill, New York (1985)

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Computational Dynamics Laboratory, Department of Mechanical Aerospace and Nuclear Engineering, Rensselaer Polytechnic Institute, 110 8th Street., Troy, NY, 12180, USA

    Rudranarayan M. Mukherjee & Kurt S. Anderson

Authors
  1. Rudranarayan M. Mukherjee
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Kurt S. Anderson
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Rudranarayan M. Mukherjee.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Mukherjee, R.M., Anderson, K.S. Orthogonal Complement Based Divide-and-Conquer Algorithm for constrained multibody systems. Nonlinear Dyn 48, 199–215 (2007). https://doi.org/10.1007/s11071-006-9083-3

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11071-006-9083-3

Keywords

Search

Navigation