Skip to main content

Advertisement

SpringerLink
Log in

Solving the Dynamic User Optimal Assignment Problem Considering Queue Spillback

  • Published:
Networks and Spatial Economics Aims and scope Submit manuscript

Abstract

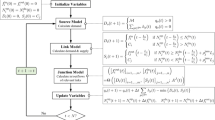
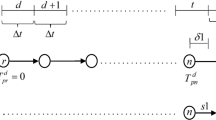
This paper studies the dynamic user optimal (DUO) traffic assignment problem considering simultaneous route and departure time choice. The DUO problem is formulated as a discrete variational inequality (DVI), with an embeded LWR-consistent mesoscopic dynamic network loading (DNL) model to encapsulate traffic dynamics. The presented DNL model is capable of capturing realistic traffic phenomena such as queue spillback. Various VI solution algorithms, particularly those based on feasible directions and a line search, are applied to solve the formulated DUO problem. Two examples are constructed to check equilibrium solutions obtained from numerical algorithms, to compare the performance of the algorithms, and to study the impacts of traffic interacts across multiple links on equilibrium solutions.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  • Arnott R, de Palma A, Lindsey R (1990) Departure time and route choice for routes in parallel. Transp Res 24B:209–228

    Article  Google Scholar 

  • Beckmann M, McGuire CB, Winsten CB (1956) Studies in the economics of transportation. Yale University Press, New Haven, CT

    Google Scholar 

  • Chabini I (1998) Discrete dynamic shortest path problems in transportation applications. Transp Res Rec 1645:170–175

    Article  Google Scholar 

  • Chen H-K, Hsueh C-F (1998) A model and an algorithm for the dynamic user-optimal route choice problem. Transp Res 32B:219–234

    Article  Google Scholar 

  • Chen A, Lo H, Yang H (2001) A self-adaptive projection and contraction algorithm for the traffic assignment problem with path-specific costs. Eur J Oper Res 135:27–41

    Article  Google Scholar 

  • Daganzo CF (1994) The cell transmission model: a dynamic representation of highway traffic consistent with the hydrodynamic theory. Transp Res 28B:269–287

    Article  Google Scholar 

  • Daganzo CF (1995) The cell transmission model, Part II: network traffic. Transp Res 29B:79–93

    Article  Google Scholar 

  • Daganzo CF (1998) Queue spillovers in transportation networks with a route choice. Transp Sci 32:3–11

    Article  Google Scholar 

  • Facchinei F, Pang J-S (2003) Finite-dimensional variational inequalities and complementarity problems, vol. I, II. Springer, New York

    Google Scholar 

  • Friesz TL, Mookherjee R (2006) Solving the dynamic network user equilibrium problem with state-dependent time shifts. Transp Res 40B:207–229

    Article  Google Scholar 

  • Friesz TL, Bernstein D, Smith TE, Tobin RL, Wei BW (1993) A variational inequality formulation of the dynamic network equilibrium problem. Operation Research 41:179–191

    Article  Google Scholar 

  • Friesz TL, Bernstein D, Suo Z, Tobin RL (2001) Dynamic network user equilibrium with state-dependent time lags. Networks and Spatial Economics 1:319–349

    Article  Google Scholar 

  • Han D, Lo H (2002) New alternating direction method for a class of nonlinear variational inequality problems. J Optim Theory Appl 112:549–560

    Article  Google Scholar 

  • He B (1997) A class of projection and contraction methods for monotone variational inequality. Appl Math Optim 35:69–76

    Google Scholar 

  • Huang HJ, Lam WHK (2002) Modeling and solving dynamic user equilibrium route and departure time choice problem in network with queues. Transp Res 36B:253–273

    Article  Google Scholar 

  • Jin WL, Zhang HM (2003) On the distribution schemes for determining flows through a merge. Transp Res 37B:521–540

    Article  Google Scholar 

  • Kuwahara M (1990) Equilibrium queuing patterns at a two-tandem bottleneck during the morning peak. Transp Sci 24:217–229

    Article  Google Scholar 

  • Lighthill MJ, Whitham JB (1955) On kinematic waves: I. Flow modeling in long rivers, II. A theory of traffic flow on long crowded roads. In Proceedings of the Roy Society A 229:291–345

  • Lo HP, Szeto WY (2002) A cell-based variational inequality formulation of the dynamic user optimal assignment problem. Transp Res 36B:421–443

    Article  Google Scholar 

  • Mahmassani H, Herman R (1984) Dynamic user equilibrium departure time and route choice on idealized traffic arterials. Transp Sci 18:362–384

    Article  Google Scholar 

  • Nagurney A (1993) Network economics: A variational inequality approach. Kluwer, Norwell, MA, USA

    Google Scholar 

  • Newell G (1987) The morning commute for non-identical travelers. Transp Sci 21:74–88

    Article  Google Scholar 

  • Nguyen S, Dupius C (1984) An efficient method for computing traffic equilibria in networks with asymmetric transportation costs. Transp Sci 18:185–202

    Article  Google Scholar 

  • Nie Y (2006) A variational inequality approach for inferring dynamic origin-destination travel demands. PhD dissertation, University of California, Davis. http://www.civil.northwestern.edu/people/nie-diss.pdf

  • Nie Y, Zhang HM (2005) Equilibrium analysis of the morning commute problem: numerical solution procedures. Journal of Mathematical and Computer Modeling, under review

  • Ran B, Hall RW, Boyce D (1996) A link-based variational inequality model for dynamic departure time/route choice. Transp Res 30B:31–46

    Article  Google Scholar 

  • Richards PI (1956) Shockwaves on the highway. Operation Research 4:42–51

    Article  Google Scholar 

  • Sheffi Y (1985) Urban transportation networks. Prentice-Hall, New Jersey

    Google Scholar 

  • Small KA (1982) The scheduling of consumer activities: work trips. Am Econ Rev 72:467–479

    Google Scholar 

  • Smith MJ (1993) A new dynamic traffic model and the existence and calculation of dynamic user equilibria on congested capacity-constrained road networks. Transp Res 26B:49–63

    Article  Google Scholar 

  • Szeto WY, Lo HP (2004) A cell-based simultaneous route and departure time choice model with elastic demand. Transp Res 38B:593–612

    Article  Google Scholar 

  • Tong CO, Wong SC (2000) A predictive dynamic traffic assignment model in congested capacity-constrained road networks. Transp Res 34B:625–644

    Article  Google Scholar 

  • Vickrey W (1969) Congestion theory and transport investment. Am Econ Rev 59:251–261

    Google Scholar 

  • Wardrop JG (1952) Some theoretical aspects of road traffic research. In Proceedings of the Institute of Civil Engineers, Part II 1:325–378

  • Wei BW, Tobin RL, Friesz TL, Bernstein D (1995) A discrete time, nested cost operator approach to the dynamic network user equilibrium problem. Transp Sci 29:79–92

    Article  Google Scholar 

  • Wei BW, Tobin RL, Carey M (2002) The existence, uniqueness and computation of an arc-based dynamic network user equilibrium formulation. Transp Res 36B:897–918

    Google Scholar 

  • Yang H, Huang H-J (1997) Analysis of the time-varying pricing of a bottleneck with elastic demand using optimal control theory. Transp Res 31B:425–440

    Article  Google Scholar 

  • Zhang HM, Nie Y (2005) Modeling network flow with and without link interaction: properties and implications. Paper presented at the 84th annual meeting of the Transportation Research Board

  • Zhu DL, P Marcotte (1993) Modified descent direction methods for solving the monotone variational inequality problem. Oper Res Lett 14:111–120

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Civil and Environmental Engineering, Northwestern University, Evanston, IL, USA

    Yu (Marco) Nie

  2. Department of Civil and Environmental Engineering, University of California, Davis, CA, 95616, USA

    H. M. Zhang

Authors
  1. Yu (Marco) Nie
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. H. M. Zhang
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Yu (Marco) Nie.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Nie, Y.(., Zhang, H.M. Solving the Dynamic User Optimal Assignment Problem Considering Queue Spillback. Netw Spat Econ 10, 49–71 (2010). https://doi.org/10.1007/s11067-007-9022-y

Download citation

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11067-007-9022-y

Keywords

Search

Navigation