A Robust Extreme Learning Machine Based on Adaptive Loss Function for Regression Modeling

Abstract

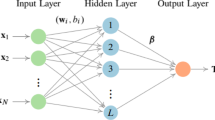
The extreme learning machine (ELM) algorithm is advantageous to regression modeling owing to its simple structure, fast computation, and good generalization performance. However, the existing ELM algorithm uses an $l_{2}$-norm loss function, which is sensitive to outliers and has low robustness. In addition, some existing robust loss functions are not sufficiently flexible to accurately estimate the relationship between sample points and loss values, resulting in unsatisfactory ELM performance. To address these problems, this study established a robust ELM (ALFELM) algorithm. First, an adaptive loss function with two tunable hyperparameters was introduced; the function can be transformed into several robust loss functions by varying the parameters. It overcomes the limitations of fixed robust loss functions. Then, the Bayesian optimization strategy was used to determine the optimal parameters of the loss function. Furthermore, the classical iterative reweighted least squares method was used to solve for output weights, with a weight function corresponding to the loss function and a regularization parameter to prevent overfitting. Finally, the proposed method was tested using several artificial and benchmark datasets, and its effectiveness was verified for a real engineering case. The results indicated that the proposed ALFELM algorithm is more robust and accurate compared with other methods, especially for a large number of outliers. In addition, the algorithm can be used to establish effective regression models for actual processes.