Skip to main content
SpringerLink
Log in

A Unified Synchronization Criterion for Reaction-Diffusion Neural Networks with Time-Varying Impulsive Delays and System Delay

  • Published:
Neural Processing Letters Aims and scope Submit manuscript

Abstract

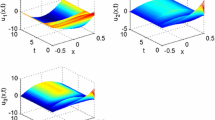
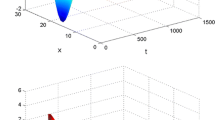
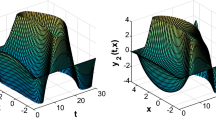
The paper mainly focuses on the synchronization of the coupled delayed reaction-diffusion neural networks (CDRDNNs) with delayed impulses. Firstly, the synchronization of CDRDNNs is studied by the direct error method instead of weighted average method. Then, a strict comparison principle is derived to solve the synchronization of the systems with delayed impulses. Combined with this comparison principle and the average impulsive delay (AID) method, some sufficient conditions of CDRDNNs are proposed. In addition, the sufficient criteria suggest that the impulsive delay could play a positive role for synchronization of CDRDNNs to a certain extent. Finally, two examples are provided to illustrate the validity of our established results.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11

Similar content being viewed by others

References

  1. Arik S (2000) Stability analysis of delayed neural networks. IEEE Trans Circuits Syst I Regul Pap 47(7):1089–1092

    Article  MathSciNet  MATH  Google Scholar 

  2. Wu W, Xiong N, Wu C (2017) Improved clustering algorithm based on energy consumption in wireless sensor networks. IET Networks 6(3):47–53

    Article  Google Scholar 

  3. Qi X, Bao H, Cao J (2019) Exponential input-to-state stability of quaternion-valued neural networks with time delay. Appl Math Comput 358:382–393

    MathSciNet  MATH  Google Scholar 

  4. Li L, Shi X, Liang J (2019) Synchronization of impulsive coupled complex-valued neural networks with delay: the matrix measure method. Neural Netw 117:285–294

    Article  MATH  Google Scholar 

  5. Strogatz S (2001) Exploring complex networks. Nature 410(6825):268–276

    Article  MATH  Google Scholar 

  6. Hu C, He H, Jiang H (2020) Synchronization of complex-valued dynamic networks with intermittently adaptive coupling: a direct error method. Automatica 112:108675

    Article  MathSciNet  MATH  Google Scholar 

  7. Wu K, Li B, Du Y, Du S (2020) Synchronization for impulsive hybrid-coupled reaction-diffusion neural networks with time-varying delays. Commun Nonlinear Sci Numer Simulat 82:105031

    Article  MathSciNet  MATH  Google Scholar 

  8. Rakkiyappan R, Gayathri D, Velmurugan G, Cao J (2019) Exponential synchronization of inertial memristor-based neural networks with time delay using average impulsive interval approach. Neural Process Lett 50:2053–2071

    Article  Google Scholar 

  9. Liu B, Lu W, Chen T (2011) Generalized Halanay inequalities and their applications to neural networks with unbounded time-varying delays. IEEE Trans Neural Networks 22(9):1508–1513

    Article  Google Scholar 

  10. Cao J, Wan Y (2014) Matrix measure strategies for stability and synchronization of inertial BAM neural network with time delays. Neural Netw 53:165–172

    Article  MATH  Google Scholar 

  11. Lu J, Jiang B, Zheng W Potential impacts of delay on stability of impulsive control systems. IEEE Transactions on Automatic Control https://doi.org/10.1109/TAC.2021.3120672, in press

  12. Lu J, Wang Z, Cao J, Ho D, Kurths J (2012) Pinning impulsive stabilization of nonlinear dynamical networks with time-varying delay. International Journal of Bifurcation and Chaos 22(7):1250176

    Article  MATH  Google Scholar 

  13. Li X, Ho D, Cao J (2019) Finite-time stability and settling-time estimation of nonlinear impulsive systems. Automatica 99:361–368

    Article  MathSciNet  MATH  Google Scholar 

  14. Lu J, Ho D, Cao J (2010) A unified synchronization criterion for impulsive dynamical networks. Automatica 46(7):1215–1221

    Article  MathSciNet  MATH  Google Scholar 

  15. Li L, Mu G (2019) Synchronization of coupled complex-valued impulsive neural networks with time delays. Neural Process Lett 50(3):2515–2527

    Article  MathSciNet  Google Scholar 

  16. He W, Qian F, Cao J (2017) Pinning-controlled synchronization of delayed neural networks with distributed-delay coupling via impulsive control. Neural Netw 85:1–9

    Article  MATH  Google Scholar 

  17. Sun Y, Li L, Liu X (2020) Exponential synchronization of neural networks with time-varying delays and stochastic impulses. Neural Netw 132:342–352

    Article  MATH  Google Scholar 

  18. Li X, Peng D, Cao J (2020) Lyapunov stability for impulsive systems via event-triggered impulsive control. IEEE Trans Autom Control 65(11):4908–4913

    Article  MathSciNet  MATH  Google Scholar 

  19. Wang Y, Lu J, Lou Y (2019) Halanay-type inequality with delayed impulses and its applications. SCIENCE CHINA Inf Sci 62(9):1–10

    Article  MathSciNet  Google Scholar 

  20. Heemels W, Teel A, Wouw N, Nešić D (2010) Networked control systems with communication constraints: tradeoffs between transmission intervals, delays and performance. IEEE Trans Autom Control 55(8):1781–1796

    Article  MathSciNet  MATH  Google Scholar 

  21. Li X, Li P (2020) Stability of time-delay systems with impulsive control involving stabilizing delays. Automatica 124:109336

    Article  MathSciNet  MATH  Google Scholar 

  22. Jiang B, Lu J, Liu Y (2020) Exponential stability of delayed systems with average-delay impulses. SIAM J Control Optim 58(6):3763–3784

    Article  MathSciNet  MATH  Google Scholar 

  23. Li X, Song S (2017) Stabilization of delay systems: delay-dependent impulsive control. IEEE Trans Autom Control 62(1):406–411

    Article  MathSciNet  MATH  Google Scholar 

  24. Li X, Song S, Wu J (2019) Exponential stability of nonlinear systems with delayed impulses and applications. IEEE Trans Autom Control 64:4024–4034

    Article  MathSciNet  MATH  Google Scholar 

  25. Wang Y, Cao J (2007) Synchronization of a class of delayed neural networks with reaction-diffusion terms. Phys Lett A 369(3):201–211

    Article  Google Scholar 

  26. Song X, Man J, Ahn C, Song S (2021) Finite-time dissipative synchronization for Markovian jump generalized inertial neural networks with reaction-diffusion terms. IEEE Transactions on Systems, Man, and Cybernetics: Systems 51(6):3650–3661

    Article  Google Scholar 

  27. Lu B, Jiang H, Hu C, Abdurahman A (2018) Pinning impulsive stabilization for BAM reaction-diffusion neural networks with mixed delays. J Franklin Inst 355:8802–8829

    Article  MathSciNet  MATH  Google Scholar 

  28. Wei T, Li X, Cao J Stability of delayed reaction-diffusion neural-network models with hybrid impulses via vector Lyapunov function. IEEE Transactions on Neural Networks and Learning Systems https://doi.org/10.1109/TNNLS.2022.3143884, in press

  29. Yang S, Jiang H, Hu C, Yu J (2021) Exponential synchronization of fractional-order reaction-diffusion coupled neural networks with hybrid delay-dependent impulses. J Franklin Inst 358:3167–3192

    Article  MathSciNet  MATH  Google Scholar 

  30. Tang Z, Xuan D, Park J, Wang Y, Feng J (2021) Impulsive effects based distributed synchronization of heterogeneous coupled neural networks. IEEE Trans Neural Netw Learn Syst 8(1):498–510

    MathSciNet  Google Scholar 

  31. Jiang B, Lou J, Lu J, Shi K Synchronization of chaotic neural networks: average-delay impulsive control. IEEE Transactions on Neural Networks and Learning Systems https://doi.org/10.1109/TNNLS.2021.3069830, in press

  32. Zhang H, Li L, Liu X (2022) Exponential synchronization of coupled neural networks under stochastic deception attacks. Neural Netw 145:189–198

    Article  Google Scholar 

  33. Lu J (2008) Global exponential stability and periodicity of reaction-diffusion delayed recurrent neural networks with Dirichlet boundary conditions. Chaos, Solitons Fractals 35:116–125

    Article  MathSciNet  MATH  Google Scholar 

  34. Lakshmikantham V, Bainov D, Simeonov P (1989) Theory of Impulsive Differential Equations. World Scientific, Singapore

    Book  Google Scholar 

  35. Yang Z, Xu D (2007) Stability analysis and design of impulsive control systems with time delay. IEEE Trans Autom Control 52(8):1448–1454

    Article  MathSciNet  MATH  Google Scholar 

  36. Ji X, Lu J, Jiang B, Shi K Distributed synchronization of delayed neural networks: delay-dependent hybrid impulsive control. IEEE Transactions on Network Science and Engineering https://doi.org/10.1109/TNSE.2021.3128244, in press

Download references

Acknowledgements

This work was supported in part by the National Natural Science Foundation of China under Grant 61503115 and 91538112.

Author information

Authors and Affiliations

  1. School of Mathematics, Hefei University of Technology, 230009, Hefei, China

    Qian Cui, Lulu Li & Wei Huang

Authors
  1. Qian Cui
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Lulu Li
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Wei Huang
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Lulu Li.

Ethics declarations

Conflict of interest

The authors declare that they have no conflict of interest.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Springer Nature or its licensor holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Cui, Q., Li, L. & Huang, W. A Unified Synchronization Criterion for Reaction-Diffusion Neural Networks with Time-Varying Impulsive Delays and System Delay. Neural Process Lett 55, 2989–3006 (2023). https://doi.org/10.1007/s11063-022-10994-4

Download citation

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11063-022-10994-4

Keywords

Search

Navigation