Skip to main content
SpringerLink
Log in

On Infinite Horizon Optimal Control Problems with a Feed Forward Neural Network Scheme

  • Published:
Neural Processing Letters Aims and scope Submit manuscript

Abstract

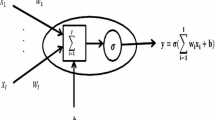
In this paper, a class of infinite-horizon nonlinear optimal control problems is considered. The main idea is to convert the infinite horizon problem to an equivalent finite-horizon optimal control problem. According to the Pontryagin minimum principle for optimal control problems and by constructing an error function, we define an unconstrained minimization problem. In the optimization problem, we use trial solutions for the state, costate and control functions where these trial solutions are constructed by using two-layer perceptron. We then minimize the error function where weights and biases associated with all neurons are unknown. Substituting the optimal values of the weights and biases into the trial solutions, we obtain the optimal solution of the original problem. We also use a dynamic optimization scheme to learning process and discuss the stability and convergence properties of it. Some examples are given to show the efficiency of the method.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8

Similar content being viewed by others

References

  1. Blot J (2009) Infinite-horizon Pontryagin principles without invertibility. J Nonlinear Convex Anal 10:177–189

    MathSciNet  MATH  Google Scholar 

  2. Blot J, Cartigny P (2000) Optimality in infinite-horizon variational problems under sign conditions. J Optim Theory Appl 106:411–419

    MathSciNet  MATH  Google Scholar 

  3. Effati S, Nazemi AR (2007) A new approach for asymptotic stability of the nonlinear ordinary differential equations. J Appl Math Comput 25:231–244

    MathSciNet  MATH  Google Scholar 

  4. Garg D, Hager WW, Rao AV (2011) Pseudospectral methods for solving infinite-horizon optimal control problems. Automatica 47:829–837

    MathSciNet  MATH  Google Scholar 

  5. Effati S, Kamyad AV, Kamyabi- Gol RA (2000) On infinite-horizon optimal control problems. Z Anal Anwend 19:269–278

    MathSciNet  MATH  Google Scholar 

  6. Jasso-Fuentes H, Hernandez-Lerma O (2008) Characterizations of overtaking optimality for controlled diffusion processes. Appl Math Optim 57:349–369

    MathSciNet  MATH  Google Scholar 

  7. Leizarowitz A (1985) Infinite horizon autonomous systems with unbounded cost. Appl Math Optim 13:19–43

    MathSciNet  MATH  Google Scholar 

  8. Mordukhovich B (1990) Minimax design for a class of distributed parameter systems. Autom Remote Control 50:1333–1340

    MATH  Google Scholar 

  9. Mordukhovich B, Shvartsman I (2004) Optimization and feedback control of constrained parabolic systems under uncertain perturbations. In: de Queiroz MS, Malisoff M, Wolenski P (eds) Optimal control, stabilization and nonsmooth analysis. Lecture notes in control and information sciences. Springer, Berlin, pp 121–132

    Google Scholar 

  10. Pickenhain S, Lykina V (2006) Sufficiency conditions for infinite horizon optimal control problems. In: Seeger A (ed) Recent advances in optimization. Proceedings of the 12th French-German-Spanish conference on optimization, Avignon. Springer, Berlin, pp 217–232

    Google Scholar 

  11. Pickenhain S, Lykina V, Wagner M (2008) On the lower semicontinuity of functionals involving Lebesgue or improper Riemann integrals in infinite horizon optimal control problems. Control Cybern 37:451–468

    MathSciNet  MATH  Google Scholar 

  12. Rapaport A, Cartigny P (2004) Turnpike theorems by a value function approach. ESAIM Control Optim Calc Var 10:123–141

    MathSciNet  MATH  Google Scholar 

  13. Rapaport A, Cartigny P (2007) Nonturnpike optimal solutions and their approximations in infinite horizon. J Optim Theory Appl 134:1–14

    MathSciNet  MATH  Google Scholar 

  14. Zaslavski AJ (2006) Turnpike properties in the calculus of variations and optimal control. Springer, New York

    MATH  Google Scholar 

  15. Anderson BDO, Moore JB (1971) Linear optimal control. Prentice-Hall, Englewood Cliffs

    MATH  Google Scholar 

  16. Leizarowitz A (1986) Tracking nonperiodic trajectories with the overtaking criterion. Appl Math Optim 14:155–171

    MathSciNet  MATH  Google Scholar 

  17. Gale D (1967) On optimal development in a multi-sector economy. Rev Econ Stud 34:1–18

    Google Scholar 

  18. Makarov VL, Rubinov AM (1977) Mathematical theory of economic dynamics and equilibria. Springer, Berlin

    MATH  Google Scholar 

  19. Zaslavski AJ (2007) Turnpike results for a discrete-time optimal control system arising in economic dynamics. Nonlinear Anal 67:2024–2049

    MathSciNet  MATH  Google Scholar 

  20. Zaslavski AJ (2009) Two turnpike results for a discrete-time optimal control systems. Nonlinear Anal 71:902–909

    MathSciNet  Google Scholar 

  21. Aubry S, Le Daeron PY (1983) The discrete Frenkel–Kontorova model and its extensions: I. Exact results for the ground-states. Physica D 8:381–422

    MathSciNet  MATH  Google Scholar 

  22. Zaslavski AJ (1987) Ground states in Frenkel–Kontorova model. Math USSR Izv 29:323–354

    MATH  Google Scholar 

  23. Coleman BD, Marcus M, Mizel VJ (1992) On the thermodynamics of periodic phases. Arch Ration Mech Anal 117:321–347

    MathSciNet  MATH  Google Scholar 

  24. Leizarowitz A, Mizel VJ (1989) One dimensional infinite horizon variational problems arising in continuum mechanics. Arch Ration Mech Anal 106:161–194

    MathSciNet  MATH  Google Scholar 

  25. Marcus M, Zaslavski AJ (1999) The structure of extremals of a class of second order variational problems. Ann Inst Henri Poincaré Anal Non Linéaire 16:593–629

    MathSciNet  MATH  Google Scholar 

  26. Blot J, Michel P (1996) First-order necessary conditions for infinite-horizon variational problems. J Optim Theory Appl 88:339–364

    MathSciNet  MATH  Google Scholar 

  27. Pontryagin LS, Boltyanski VS, Gamkrelidze RV, Mischenko EF (1962) The mathematical theory of optimal processes. Wiley, New York

    Google Scholar 

  28. Carlson DA, Haurie A (1987) Infinite-horizon optimal control. Lecture notes in economics and mathematical systems, vol 290. Springer, Germany

    Google Scholar 

  29. Smirnov GV (1996) Transversality condition for infinite-horizon problems. J Optim Theory Appl 88:671–688

    MathSciNet  MATH  Google Scholar 

  30. Aubin JP, Clarke FH (1976) Shadow prices and duality for a class of optimal control problems. SIAM J Control Optim 17:567–587

    MathSciNet  MATH  Google Scholar 

  31. Michel P (1992) On the transversality condition in infinite-horizon optimal problems. Econometrica 50:976–985

    MathSciNet  Google Scholar 

  32. Ye JJ (1993) Non-smooth maximum principle for infinite-horizon problems. J Optim Theory Appl 76:485–500

    MathSciNet  MATH  Google Scholar 

  33. Ekeland I (1988) some variational problems arising from mathematical economic. Lect Notes Math 1330:1–18

    MathSciNet  MATH  Google Scholar 

  34. Nazemi AR, Mahmoudy N (2014) Solving infinite horizon optimal control problems using the Haar wavelet collocation method. ANZIAM J 56:179–191

    MathSciNet  MATH  Google Scholar 

  35. Fahroo F, Ross IM (2008) Pseudospectral methods for infinite-horizon optimal control problems. J Guid Control Dyn 31:927–936

    Google Scholar 

  36. Schalkoff RJ (1997) Artificial neural networks. McGraw-Hill, New York

    MATH  Google Scholar 

  37. Minsky M, Papert S (1969) Perceptrons. MIT Press, Cambridge

    MATH  Google Scholar 

  38. Khanna T (1990) Foundations of neural networks. Addison-Wesley, Reading

    MATH  Google Scholar 

  39. Stanley J (1990) Introduction to neural networks, 3rd edn. Sierra Mardre Press, Sierra Madre

    Google Scholar 

  40. Lippmann RP (1987) An introduction to computing with neural nets. IEEE ASSP Mag 4:4–22

    Google Scholar 

  41. Hornick K, Stinchcombe M, White H (1989) Multilayer feedforward networks are universal approximators. Neural Netw 2(5):359–366

    MATH  Google Scholar 

  42. Lapedes A, Farber R (1988) How neural nets work? In: Anderson DZ (ed) Neural information processing systems, AIP. Springer, New York, pp 442–456

    Google Scholar 

  43. Mckeown JJ, Stella F, Hall G (1997) Some numerical aspects of the training problem for feed-forward neural nets. Neural Netw 10(8):1455–1463

    Google Scholar 

  44. Haykin S (2007) Neural networks: a comprehensive foundation, 3rd edn. Prentice-Hall, Upper Saddle River

    MATH  Google Scholar 

  45. Graupe D (2007) Principles of artificial neural networks, 2nd edn. World Scientific, Singapore

    MATH  Google Scholar 

  46. Tang H, Tan KC, Yi Z (2007) Neural networks: computational models and applications. Springer, Berlin

    MATH  Google Scholar 

  47. Muller B, Reinhardt J, Strickland MT (2002) Neural networks: an introduction, 2nd edn. Springer, Berlin

    MATH  Google Scholar 

  48. Picton P (2000) Neural networks, 2nd edn. Palgrave, Great Britain

    Google Scholar 

  49. Fine TL (1999) Feed forward neural network methodology. Springer, New York

    Google Scholar 

  50. Ellacott SW (1997) Mathematics of neural networks: models, algorithms and applications. Kluwer Academic Publishers, Boston

    Google Scholar 

  51. Lagaris IE, Likas A, Fotiadis DI (1998) Artificial neural networks for solving ordinary and partial differential equations. IEEE Trans Neural Netw 9:987–1000

    Google Scholar 

  52. Malek A, Shekari Beidokhti R (2006) Numerical solution for high order differential equations using a hybrid neural network. Optim Method Appl Math Comput 183:260–271

    MathSciNet  MATH  Google Scholar 

  53. Shekari Beidokhti R, Malek A (2009) Solving initial-boundary value problems for systems of partial differential equations using neural networks and optimization techniques. J Frankl Inst 346:898–913

    MathSciNet  MATH  Google Scholar 

  54. Tsoulos IG, Gavrilis D, Glavas E (2009) Solving differential equations with constructed neural networks. Neurocomputing 72:2385–2391

    Google Scholar 

  55. Kumar M, Yadav N (2011) Multilayer perceptrons and radial basis function neural network methods for the solution of differential equations: a survey. Comput Math Appl 62:3796–3811

    MathSciNet  MATH  Google Scholar 

  56. Dua V (2011) An artificial neural network approximation based decomposition approach for parameter estimation of system of ordinary differential equations. Comput Chem Eng 35:545–553

    Google Scholar 

  57. Shirvany Y, Hayati M, Moradian R (2008) Numerical solution of the nonlinear Schrodinger equation by feedforward neural networks. Commun Nonlinear Sci Numer Simul 13:2132–2145

    MathSciNet  MATH  Google Scholar 

  58. Shirvany Y, Hayati M, Moradian R (2009) Multilayer perceptron neural networks with novel unsupervised training method for numerical solution of the partial differential equations. Appl Soft Comput 9:20–29

    Google Scholar 

  59. Balasubramaniam P, Kumaresan N (2008) Solution of generalized matrix Riccati differential equation for indefinite stochastic linear quadratic singular system using neural networks. Appl Math Comput 204:671–679

    MathSciNet  MATH  Google Scholar 

  60. Becerikli Y, Konarm AF, Samad T (2003) Intelligent optimal control with dynamic neural networks. Neural Netw 16:251–259

    Google Scholar 

  61. Vrabie D, Lewis F (2009) Neural network approach to continuous-time direct adaptive optimal control for partially unknown nonlinear systems. Neural Netw 22:237–246

    MATH  Google Scholar 

  62. Vrabie D, Lewis F, Levine D (2008) Neural network-based adaptive optimal controller—a continuous-time formulation. Commun Comput Inf Sci 15:276–285

    MATH  Google Scholar 

  63. Cheng T, Lewis FL, Abu-Khalaf M (2007) Fixed-final-time-constrained optimal control of nonlinear systems using neural network HJB approach. IEEE Trans Neural Netw 18:1725–1737

    Google Scholar 

  64. Effati S, Pakdaman M (2013) Optimal control problem via neural networks. Neural Comput Appl 23:2093–2100

    Google Scholar 

  65. Nazemi AR (2011) A dynamical model for solving degenerate quadratic minimax problems with constraints. J Comput Appl Math 236:1282–1295

    MathSciNet  MATH  Google Scholar 

  66. Nazemi AR (2012) A dynamic system model for solving convex nonlinear optimization problems. Commun Nonlinear Sci Numer Simul 17:1696–1705

    MathSciNet  MATH  Google Scholar 

  67. Nazemi AR (2013) Solving general convex nonlinear optimization problems by an efficient neurodynamic model. Eng Appl Artif Intell 26:685–696

    Google Scholar 

  68. Nazemi AR, Omidi F (2012) A capable neural network model for solving the maximum flow problem. J Comput Appl Math 236:3498–3513

    MathSciNet  MATH  Google Scholar 

  69. Nazemi AR (2014) A neural network model for solving convex quadratic programming problems with some applications. Eng Appl Artif Intell 32:54–62

    Google Scholar 

  70. Nazemi AR, Omidi F (2013) An efficient dynamic model for solving the shortest path problem. Transp Res C 26:1–19

    Google Scholar 

  71. Nazemi AR, Sharifi E (2013) Solving a class of geometric programming problems by an efficient dynamic model. Commun Nonlinear Sci Numer Simul 18:692–709

    MathSciNet  MATH  Google Scholar 

  72. Nazemi AR, Effati S (2013) An application of a merit function for solving convex programming problems. Comput Ind Eng 66:212–221

    Google Scholar 

  73. Nazemi AR, Nazemi M (2014) A gradient-based neural network method for solving strictly convex quadratic programming problems. Cogn Comput 6:484–495

    Google Scholar 

  74. Bohner M, Kenzhebaev K, Lavrova O, Stanzhytskyi O (2017) Pontryagin’s maximum principle for dynamic systems on time scales. J Differ Equ Appl 23:1161–1189

    MathSciNet  MATH  Google Scholar 

  75. Ferreira MMA, Ribeiro AF, Smirnov GV (2015) Local minima of quadratic functionals and control of hydro-electric power stations. JOTA J Optim Theory Appl 165:985–1005

    MathSciNet  MATH  Google Scholar 

  76. Hartl RF, Sethi SP, Vickson RG (1995) A survey of the maximum pipnciples for optimal control problems with state constraints. SIAM Rev 37:181–218

    MathSciNet  MATH  Google Scholar 

  77. Cybenko G (1989) Approximation by superpositions of a sigmoidal function. Math Control Signals Syst 2:303–314

    MathSciNet  MATH  Google Scholar 

  78. Bazaraa MS, Sherali HD, Shetty CM (2006) Nonlinear programming—theory and algorithms, 3rd edn. Wiley, Hoboken

    MATH  Google Scholar 

  79. Zhang X-S (2000) Neural networks in optimization. Kluwer Academic Publishers, Dordrecht

    MATH  Google Scholar 

  80. Nocedal J, Wright S (2006) Numerical optimization, 2nd edn. Springer, Berlin

    MATH  Google Scholar 

  81. Lee KY, El-Sharkawi M (2007) A modern heuristic optimization techniques: theory and applications to power systems. Wiley, New York

    Google Scholar 

  82. Miller RK, Michel AN (1982) Ordinary differential equations. Academic Press, New York

    MATH  Google Scholar 

  83. Sun J, Chen J-S, Ko C-H (2012) Neural networks for solving second-order cone constrained variational inequality problem. Comput Optim Appl 51:623–648

    MathSciNet  MATH  Google Scholar 

  84. Hale JK (1969) Ordinary differential equations. Wiley, New York

    MATH  Google Scholar 

  85. Jajarmi A, Pariz N, Effati S, Kamyad AV (2011) Solving infinite horizon nonlinear optimal control problems using an extended modal series method. J Zhejiang Univ Sci C (Comput Electron) 12:667–677

    Google Scholar 

Download references

Funding

This study was not funded by any grant.

Author information

Authors and Affiliations

  1. Faculty of Mathematical Sciences, Shahrood University of Technology, Shahrood, Iran

    Marziyeh Mortezaee & Alireza Nazemi

Authors
  1. Marziyeh Mortezaee
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Alireza Nazemi
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Alireza Nazemi.

Ethics declarations

Conflict of interest

The authors declare that they have no conflict of interest.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Mortezaee, M., Nazemi, A. On Infinite Horizon Optimal Control Problems with a Feed Forward Neural Network Scheme. Neural Process Lett 51, 449–471 (2020). https://doi.org/10.1007/s11063-019-10099-5

Download citation

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11063-019-10099-5

Keywords

Search

Navigation