Skip to main content
SpringerLink
Log in

Memory-based State Estimation of T–S Fuzzy Markov Jump Delayed Neural Networks with Reaction–Diffusion Terms

  • Published:
Neural Processing Letters Aims and scope Submit manuscript

Abstract

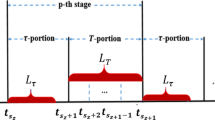
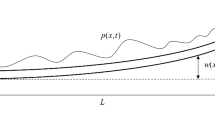
This paper investigates the problem of state estimation for Takagi–Sugeno (T–S) fuzzy Markov jump delayed neural networks with reaction–diffusion terms. A memory-based control scheme that contains a constant signal transmission delay is adopted, which is the first attempt to handle the issue of state estimation for fuzzy neural networks. Firstly, several conditions that guarantee the stability of the considered system are derived. Then, the fuzzy memory-based controller design scheme is proposed. Finally, three numerical examples are given to demonstrate the validity of the proposed method.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5

Similar content being viewed by others

References

  1. Shi P, Zhang Y, Chadli M, Agarwal RK (2016) Mixed H-infinity and passive filtering for discrete fuzzy neural networks with stochastic jumps and time delays. IEEE Trans Neural Netw Learn 27(4):903–909

    MathSciNet  Google Scholar 

  2. You GW, Park S, Oh D (2017) Diagnosis of electric vehicle batteries using recurrent neural networks. IEEE Trans Ind Electron 64(6):4885–4893

    Google Scholar 

  3. Xu Z, Su H, Shi P, Lu R, Wu ZG (2017) Reachable set estimation for Markovian jump neural networks with time-varying delays. IEEE Trans Cybern 47(10):3208–3217

    Google Scholar 

  4. Manivannan R, Panda S, Chong KT, Cao J (2018) An Arcak-type state estimation design for time-delayed static neural networks with leakage term based on unified criteria. Neural Netw 106(C):110–126

    Google Scholar 

  5. Huang Y, Chen W, Ren S, Zheng Z (2018) Analysis and pinning control for generalized synchronization of delayed coupled neural networks with different dimensional nodes. J Frankl Inst 355(13):5968–5997

    MathSciNet  MATH  Google Scholar 

  6. Li X, Zhu Q, O’Regan D (2014) pth Moment exponential stability of impulsive stochastic functional differential equations and application to control problems of NNs. J Frankl Inst 351(9):4435–4456

    MATH  Google Scholar 

  7. Singh V (2007) Some remarks on global asymptotic stability of neural networks with constant time delay. Chaos Solitons Fractals 32(5):1720–1724

    MathSciNet  MATH  Google Scholar 

  8. Li X, Fu X (2012) Lag synchronization of chaotic delayed neural networks via impulsive control. IMA J Math Control Inf 29(1):133–145

    MathSciNet  MATH  Google Scholar 

  9. Ge C, Hua C, Guan X (2017) New delay-dependent stability criteria for neural networks with time-varying delay using delay-decomposition approach. IEEE Trans Neural Netw Learn Syst 25(7):1378–1383

    Google Scholar 

  10. Liu Y, Ju HP, Fang F (2018) Global exponential stability of delayed neural networks based on a new integral inequality. IEEE Trans Syst Man Cybern Syst. https://doi.org/10.1109/TSMC.2018.2815560

    Google Scholar 

  11. Ma Q, Feng G, Xu S (2013) Delay-dependent stability criteria for reaction-diffusion neural networks with time-varying delays. IEEE Trans Cybern 43(6):1913–1920

    Google Scholar 

  12. Liu D, Wang L, Pan Y, Ma H (2016) Mean square exponential stability for discrete-time stochastic fuzzy neural networks with mixed time-varying delay. Neurocomputing 171(C):1622–1628

    Google Scholar 

  13. Yan H, Hao Z, Yang F, Zhan X, Chen P (2018) Event-triggered asynchronous guaranteed cost control for Markov jump discrete-time neural networks with distributed delay and channel fading. IEEE Trans Neural Netw Learn Syst 29(8):3588–3598

    MathSciNet  Google Scholar 

  14. Xu Y, Lu R, Shi P, Tao J, Xie S (2018) Robust estimation for neural networks with randomly occurring distributed delays and Markovian jump coupling. IEEE Trans Neural Netw Learn Syst. https://doi.org/10.1109/TNNLS.2016.2636325

    MathSciNet  Google Scholar 

  15. Li F, Shen H (2015) Finite-time \({H}_\infty \) synchronization control for semi-Markov jump delayed neural networks with randomly occurring uncertainties. Neurocomputing 166:447–454

    Google Scholar 

  16. Wang DY, Li LS (2016) Mean-square stability analysis of discrete-time stochastic Markov jump recurrent neural networks with mixed delays. Neurocomputing 189:171–178

    Google Scholar 

  17. Wu Z, Su H, Chu J (2010) State estimation for discrete Markovian jumping neural networks with time delay. Neurocomputing 73(10):2247–2254

    Google Scholar 

  18. Shen H, Zhu Y, Zhang L, Park JH (2016) Extended dissipative state estimation for Markov jump neural networks with unreliable links. IEEE Trans Neural Netw Learn Syst 28(2):346–358

    MathSciNet  Google Scholar 

  19. Shi G, Ma Q (2012) Synchronization of stochastic Markovian jump neural networks with reaction-diffusion terms. Neurocomputing 77(1):275–280

    Google Scholar 

  20. Dharani S, Rakkiyappan R, Cao J, Alsaedi A (2017) Synchronization of generalized reaction-diffusion neural networks with time-varying delays based on general integral inequalities and sampled-data control approach. Cogn Neurodyn 11(4):1–13

    Google Scholar 

  21. Wang Y, Cao J (2007) Synchronization of a class of delayed neural networks with reaction diffusion terms. Phys Lett A 369(3):201–211

    Google Scholar 

  22. Sheng L, Yang H, Lou X (2009) Adaptive exponential synchronization of delayed neural networks with reaction-diffusion terms. Chaos Solitons Fractals 40(2):930–939

    MathSciNet  MATH  Google Scholar 

  23. Chen Z, Fu X, Zhao D (2013) Anti-periodic mild attractor of delayed hopfield neural networks systems with reaction-diffusion terms. Neurocomputing 99(1):372–380

    Google Scholar 

  24. Li R, Wei H (2016) Synchronization of delayed Markovian jump memristive neural networks with reaction-diffusion terms via sampled data control. Int J Mach Learn Cybern 7(1):157–169

    Google Scholar 

  25. Wei T, Wang Y, Wang L (2017) Robust exponential synchronization for stochastic delayed neural networks with reaction-diffusion terms and Markovian jumping parameters. Neural Process Lett 3:1–16

    Google Scholar 

  26. Rakkiyappan (2017) Sampled-data synchronization of randomly coupled reactioncdiffusion neural networks with Markovian jumping and mixed delays using multiple integral approach. Neural Comput Appl 28(3):449–462

    Google Scholar 

  27. Li H, Chen B, Zhou Q, Qian W (2009) Robust stability for uncertain delayed fuzzy Hopfield neural networks with Markovian jumping parameters. IEEE Trans Syst Man Cybern Part B 39(1):94–102

    Google Scholar 

  28. Balasubramaniam P, Rakkiyappan R, Sathy R (2011) Delay dependent stability results for fuzzy BAM neural networks with Markovian jumping parameters. Expert Syst Appl 38(1):121–130

    MATH  Google Scholar 

  29. Ali MS, Vadivel R (2018) Decentralized event-triggered exponential stability for uncertain delayed genetic regulatory networks with Markov jump parameters and distributed delays. Neural Process Lett 47(3):1219–1252

    Google Scholar 

  30. Han W, Liu Y, Wang L (2012) Global exponential stability of delayed fuzzy cellular neural networks with Markovian jumping parameters. Neural Comput Appl 21(1):67–72

    Google Scholar 

  31. Zheng CD, Zhang X, Wang Z (2016) Mode and delay-dependent stochastic stability conditions of fuzzy neural networks with Markovian jump parameters. Neural Process Lett 43(1):195–217

    Google Scholar 

  32. Tong D, Zhu Q, Zhou W, Xu Y, Fang J (2013) Adaptive synchronization for stochastic T–S fuzzy neural networks with time-delay and Markovian jumping parameters. Neurocomputing 117(14):91–97

    Google Scholar 

  33. Ahn CK (2010) Delay-dependent state estimation for T-S fuzzy delayed Hopfield neural networks. Nonlinear Dyn 61(3):483–489

    MathSciNet  MATH  Google Scholar 

  34. Ali MS, Gunasekaran N, Zhu Q (2017) State estimation of T-S fuzzy delayed neural networks with Markovian jumping parameters using sampled-data control. Fuzzy Sets Syst 306:87–104

    MathSciNet  MATH  Google Scholar 

  35. Li X, Rakkiyappan R (2011) Robust asymptotic state estimation of TakagiCSugeno fuzzy Markovian jumping Hopfield neural networks with mixed interval time varying delays. Math Methods Appl Sci 34(17):2197–2207

    MathSciNet  MATH  Google Scholar 

  36. Lim C, Kim J, Han S, Park J (1996) Design of neural networks with the hidden-layer control part and memory part. In: IEEE IECON international conference on industrial electronics, control, and instrumentation, pp 893–897

  37. Liu Y, Guo BZ, Park JH, Lee SM (2018) Nonfragile exponential synchronization of delayed complex dynamical networks with memory sampled-data control. IEEE Trans Neural Netw Learn Syst 29(1):118–128

    MathSciNet  Google Scholar 

  38. Ran S, Xue Y, Zheng BC, Wang Z (2017) Quantized feedback fuzzy sliding mode control design via memory-based strategy. Appl Math Comput 298:283–295

    MathSciNet  MATH  Google Scholar 

  39. Xie YF, Gui WH, Wang YL, Jiang ZH (2009) Memory state feedback controller design for singular systems with multiple internal constant point delays. IET Control Theory Appl 3(6):631–641

    MathSciNet  Google Scholar 

  40. Liu Y, Ju HP, Guo BZ, Shu Y (2018) Further results on stabilization of chaotic systems based on fuzzy memory sampled-data control. IEEE Trans Fuzzy Syst 26(2):1040–1045

    Google Scholar 

  41. Zhang R, Zeng D, Ju HP, Liu Y, Zhong S (2018) A new approach to stabilization of chaotic systems with nonfragile fuzzy proportional retarded sampled-data control. IEEE Trans Cybern. https://doi.org/10.1109/TCYB.2018.2831782

    Google Scholar 

  42. Shen H, Huang X, Zhou J, Wang Z (2012) Global exponential estimates for uncertain Markovian jump neural networks with reaction-diffusion terms. Nonlinear Dyn 69(1–2):473–486

    MathSciNet  MATH  Google Scholar 

  43. Ozcan N, Ali MS, Yogambigai J, Zhu Q, Arik S (2018) Robust synchronization of uncertain Markovian jump complex dynamical networks with time-varying delays and reaction-diffusion terms via sampled-data control. J Frankl Inst 355(3):1192–1216

    MathSciNet  MATH  Google Scholar 

  44. Li H, Zhou Q, Chen B, Liu H (2011) Parameter-dependent robust stability for uncertain Markovian jump systems with time delay. J Frankl Inst 348(4):738–748

    MathSciNet  MATH  Google Scholar 

  45. Chen J, Gu K, Kharitonov VL (2003) Stability of time-delay systems. Birkhauser, Boston

    MATH  Google Scholar 

  46. Manivannan R, Samidurai R, Cao J, Alsaedi A, Alsaadi FE (2017) Global exponential stability and dissipativity of generalized neural networks with time-varying delay signals. Neural Netw 87:149–159

    MATH  Google Scholar 

  47. Manivannan R, Samidurai R, Cao J, Alsaedi A, Alsaadi FE (2018) Design of extended dissipativity state estimation for generalized neural networks with mixed time-varying delay signals. Inf Sci 424:175–203

    MathSciNet  Google Scholar 

Download references

Acknowledgements

This work was supported by the National Natural Science Foundation of China under Grant U1604146, and by the Foundation for the University Technological Innovative Talents of Henan Province under Grant 18HASTIT019.

Author information

Authors and Affiliations

  1. School of Information Engineering, Henan University of Science and Technology, Luoyang, 471023, China

    Xiaona Song, Jingtao Man, Zhumu Fu & Mi Wang

  2. School of Electrical and Automation Engineering, Nanjing Normal University, Nanjing, 210042, China

    Junwei Lu

Authors
  1. Xiaona Song
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Jingtao Man
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Zhumu Fu
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Mi Wang
    View author publications

    You can also search for this author in PubMed Google Scholar

  5. Junwei Lu
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Xiaona Song.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Song, X., Man, J., Fu, Z. et al. Memory-based State Estimation of T–S Fuzzy Markov Jump Delayed Neural Networks with Reaction–Diffusion Terms. Neural Process Lett 50, 2529–2546 (2019). https://doi.org/10.1007/s11063-019-10026-8

Download citation

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11063-019-10026-8

Keywords

Search

Navigation