Abstract
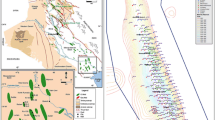
Resource estimation of a placer deposit is always a difficult and challenging job because of high variability in the deposit. The complexity of resource estimation increases when drill-hole data are sparse. Since sparsely sampled placer deposits produce high-nugget variograms, a traditional geostatistical technique like ordinary kriging sometimes fails to produce satisfactory results. In this article, a machine learning algorithm—the support vector machine (SVM)—is applied to the estimation of a platinum placer deposit. A combination of different neighborhood samples is selected for the input space of the SVM model. The trade-off parameter of the SVM and the bandwidth of the kernel function are selected by genetic algorithm learning, and the algorithm is tested on a testing data set. Results show that if eight neighborhood samples and their distances and angles from the estimated point are considered as the input space for the SVM model, the developed model performs better than other configurations. The proposed input space-configured SVM model is compared with ordinary kriging and the traditional SVM model (location as input) for resource estimation. Comparative results reveal that the proposed input space-configured SVM model outperforms the other two models.










Similar content being viewed by others
References
Bishop, C. M., 1995, Neural networks for pattern recognition: Oxford University Press, New York.
Caers, J., 2001, Automatic histogram and variogram reproduction in simulated annealing simulation: Math. Geol., v. 33, no. 2, p. 167–190.
Chatterjee, S., and Bandopadhyay, S., 2007, Global neural network learning using genetic algorithm for ore grade prediction of iron ore deposit: Miner. Resour. Eng., v. 12, no. 4, p. 258–269.
Chatterjee, S., Bandopadhyay, S., and Rai, P., 2008a, A genetic algorithm based neural network learning parameter selection approach for ore grade evaluation of a limestone deposit: Min. Technol., v. 117, no. 4, p. 178–190.
Chatterjee, S., Bandopadhyay, S., and Machuca, D., 2008b, Ore waste classification of a lead zinc deposit using support vector machine: SME Trans., v. 34, p. 94–103.
Chatterjee, S., Bandopadhyay, S., and Machuca, D., 2010, Ore grade prediction using genetic algorithm and clustering based ensemble neural network model: Math. Geosci., v. 42, no. 3, p. 309–326.
Chatterjee, S., Bhattacherjee, A., Samanta, B., and Pal, S. K., 2006, Ore grade estimation of a limestone deposit in India using an artificial neural network: Appl. GIS, v. 2, no. 1, p. 2.1–2.20.
Cressie, N. A. C., 1985, Fitting variogram models by weighted least squares: Math. Geol., v. 17, p. 563–586.
DeJong, K., 1975, An analysis of the behavior of a class of genetic adaptive systems. Ph.D. dissertation, Department of Computer and Communication Sciences, University of Michigan.
Deutsch, C., and Journel, A., 1998, GSLIB: geostatistical software library (2nd edn.): Oxford University Press, New York.
Dutta, S., Bandopadhyay, S., Ganguli, R., and Misra, R., 2010, Machine learning algorithms and their application to ore reserve estimation of sparse and imprecise data: J. Intell. Learn. Syst. Appl., v. 2, p. 86–96.
Genton, M. G., 2001, Classes of kernels for machine learning: a statistics perspective: J. Mach. Learn. Res., v. 2, p. 299–312.
Goldberg, D. E., 1989, Genetic algorithms in search, optimization and machine learning: Addison-Wesley, Reading.
Goovaerts, P., 1997, Geostatistics for natural resources evaluation: Oxford University Press, New York.
Haykins, S., 1999, Neural networks: a comprehensive foundation (2nd edn.): Prentice Hall, New Jersey, 824 p.
Hofmann, T., Schölkopf, B., and Smola, A. J., 2008, Kernel methods in machine learning: Ann. Statist., v. 36, no. 3, p. 1171–1220.
Hsieh, W. W., 2009, Machine learning methods in the environmental sciences: neural networks and kernels: Cambridge University Press, Cambridge, 364 p.
Kanevski, M., 2008, Advanced mapping of environmental data geostatistics, machine learning and bayesian maximum entropy (edited book): ISTE and Wiley, London, 328 p.
Kanevski, M., Pozdnoukhov, A., and Timonin, V., 2009, Machine learning for spatial environmental data theory, applications, and software: EPFL Press, Lausanne, Switzerland, 400 p.
Kapageridis, I. K., 1999, Application of artificial neural network systems to grade estimation from exploration data. Ph.D. dissertation, School of Chemical, Environmental and Mining Engineering, University of Nottingham, Nottingham, 260 p.
Kapageridis, I. K., 2005, Input space configuration effects in neural network-based grade estimation: Comput. Geosci., v. 31, no. 6, p. 704–711.
Koike, K., Matsuda, S., and Gu, B., 2001, Evaluation of interpolation accuracy of neural kriging with application to temperature-distribution analysis: Math. Geol., v. 28, p. 421–448.
Koike, K., Matsuda, S., Suzuki, T., and Ohmi, M., 2002, Neural network-based estimation of principal metal contents in the Hokuroku district, northern Japan, for exploring Kuroko-type deposits: Nat. Resour. Res., v. 11, no. 2, p. 135–156.
Nash, J. E., and Sutcliffe, J. V., 1970, River flow forecasting through conceptual models, Part I. A discussion of principles: J. Hydrol., v. 10, p. 282–290.
Samanta, B., and Bandopadhyay, S., 2009, Construction of a radial basis function using evolutionary algorithm for grade estimation in placer gold deposit: Comput. Geosci., v. 19, no. 4, p. 567–575.
Samanta, B., Bandopadhyay, S., and Ganguli, R., 2004, Data segmentation and genetic algorithms for sparse data division in Nome placer grade estimation using neural network and geostatistics: Explor. Min. Geol., v. 11, p. 69–76.
Samanta, B., Ganguli, R., and Bandopadhyay, S., 2005, Comparing the predictive performance of neural network technique with ordinary kriging technique in a bauxite deposit: Trans. Inst. Min. Metall., v. 114, p. A1–A12.
Samanta, B., Bandopadhyay, S., and Ganguli, R., 2006, Comparative evaluation of neural network learning algorithms for ore grade estimation: Math. Geol., v. 38, no. 2, p. 175–197.
Suykens, J. A. K., Gestel, T. V., De Brabanter, J., De Moor, B., and Vandewalle, J., 2002, Least squares support vector machines: World Scientific, Singapore, 308 p.
Vapnik, V. N., 1995, The nature of statistical learning theory: Springer, New York.
Yama, B. R., and Lineberry, G. T., 1999, Artificial neural network application for a predictive task in mining: Min. Eng., v. 51, no. 2, p. 59–64.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Chatterjee, S., Bandopadhyay, S. Goodnews Bay Platinum Resource Estimation Using Least Squares Support Vector Regression with Selection of Input Space Dimension and Hyperparameters. Nat Resour Res 20, 117–129 (2011). https://doi.org/10.1007/s11053-011-9140-6
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11053-011-9140-6