Emulating cellular automata in chemical reaction–diffusion networks

Abstract

Chemical reactions and diffusion can produce a wide variety of static or transient spatial patterns in the concentrations of chemical species. Little is known, however, about what dynamical patterns of concentrations can be reliably programmed into such reaction–diffusion systems. Here we show that given simple, periodic inputs, chemical reactions and diffusion can reliably emulate the dynamics of a deterministic cellular automaton, and can therefore be programmed to produce a wide range of complex, discrete dynamics. We describe a modular reaction–diffusion program that orchestrates each of the fundamental operations of a cellular automaton: storage of cell state, communication between neighboring cells, and calculation of cells’ subsequent states. Starting from a pattern that encodes an automaton’s initial state, the concentration of a “state” species evolves in space and time according to the automaton’s specified rules. To show that the reaction–diffusion program we describe produces the target dynamics, we simulate the reaction–diffusion network for two simple one-dimensional cellular automata using coupled partial differential equations. Reaction–diffusion based cellular automata could potentially be built in vitro using networks of DNA molecules that interact via branch migration processes and could in principle perform universal computation, storing their state as a pattern of molecular concentrations, or deliver spatiotemporal instructions encoded in concentrations to direct the behavior of intelligent materials.

Appendices

Rule 110 chemical reactions (synonymous with Sect. 8)

This section describes the complete set of abstract chemical reactions that govern our Rule 110 chemical automaton. These chemical reactions can be converted into a set of coupled partial differential equations and solved to observe how the system behaves over time (see Section 8). Figure 10 shows a detail of the circuit from Fig. 7 for a Rule 110 automaton, with each chemical species labeled.

Fig. 10

Chemical reaction–diffusion circuit for Rule 110. This is a detailed version of the circuit outlined in Fig. 7, using the modules defined in Fig. 2. Species are labelled in red by their equation numbers from Section 8., with species names and abbreviations to the right

• 1. Communication stage

  • a. Broadcasting:

    $$SrcA+keyA+Last\mathop {\rightarrow {}}\limits ^{k_{B}}SrcA+SigA+keyA+Last$$

    (7.1)
    $$SigA\mathop {\rightarrow {}}\limits ^{k_{Bd}}waste $$

    (7.2)
    $$SrcB+keyB+Last\mathop {\rightarrow {}}\limits ^{k_{B}}SrcB+SigB+keyB+Last $$

    (7.3)
    $$SigB\mathop {\rightarrow {}}\limits ^{k_{Bd}}waste $$

    (7.4)
    $$SrcC+keyC+Last\mathop {\rightarrow {}}\limits ^{k_{B}}SrcC+SigC+keyC+Last $$

    (7.5)
    $$SigC\mathop {\rightarrow {}}\limits ^{k_{Bd}}waste $$

    (7.6)
    $$SrcD+keyD+Last\mathop {\rightarrow {}}\limits ^{k_{B}}SrcD+SigD+keyD+Last $$

    (7.7)
    $$SigD\mathop {\rightarrow {}}\limits ^{k_{Bd}}waste $$

    (7.8)

  • a. Receiving and processing left-hand signal:

    $$SigD+keyA\mathop {\rightarrow {}}\limits ^{k_{x}}SigD+Lraw+keyA $$

    (7.9)
    $$SigA+keyB\mathop {\rightarrow {}}\limits ^{k_{x}}SigA+Lraw+keyB $$

    (7.10)
    $$SigB+keyC\mathop {\rightarrow {}}\limits ^{k_{x}}SigB+Lraw+keyC $$

    (7.11)
    $$SigC+keyD\mathop {\rightarrow {}}\limits ^{k_{x}}SigC+Lraw+keyD $$

    (7.12)
    $$Lraw\mathop {\longrightarrow {}}\limits ^{4*k_{x}}waste $$

    (7.13)
    $$source\mathop {\longrightarrow {}}\limits ^{c_{recTh}*k_{p}}ThL\mathop {\rightarrow {}}\limits ^{k_{x}}waste $$

    (7.14)
    $$source\mathop {\rightarrow {}}\limits ^{k_{p}}AmpL\mathop {\rightarrow {}}\limits ^{k_{x}}waste $$

    (7.15)
    $$Lraw+ThL\mathop {\rightarrow {}}\limits ^{k_{T}}waste $$

    (7.16)
    $$Lraw+AmpL\mathop {\rightarrow {}}\limits ^{k_{L}}Lraw+Lft $$

    (7.17)
    $$Lft\mathop {\rightarrow {}}\limits ^{k_{x}}waste $$

    (7.18)

  • a. Receiving and processing right-hand signal:

    $$SigB+keyA\mathop {\rightarrow {}}\limits ^{k_{x}}SigB+Rraw+keyA $$

    (7.19)
    $$SigC+keyB\mathop {\rightarrow {}}\limits ^{k_{x}}SigC+Rraw+keyB $$

    (7.20)
    $$SigD+keyC\mathop {\rightarrow {}}\limits ^{k_{x}}SigD+Rraw+keyC $$

    (7.21)
    $$SigA+keyD\mathop {\rightarrow {}}\limits ^{k_{x}}SigA+Rraw+keyD $$

    (7.22)
    $$Rraw\mathop {\longrightarrow {}}\limits ^{4*k_{x}}waste $$

    (7.23)
    $$source\mathop {\longrightarrow {}}\limits ^{c_{recTh}*k_{p}}Thr\mathop {\longrightarrow {}}\limits ^{k_{x}}waste $$

    (7.24)
    $$source\mathop {\longrightarrow {}}\limits ^{k_{p}}Ampr\mathop {\longrightarrow {}}\limits ^{k_{x}}waste $$

    (7.25)
    $$Rraw+Thr\mathop {\longrightarrow {}}\limits ^{k_{T}}waste $$

    (7.26)
    $$Rraw+Ampr\mathop {\longrightarrow {}}\limits ^{k_{L}}Rraw+Rght $$

    (7.27)
    $$Rght\mathop {\longrightarrow {}}\limits ^{k_{x}}waste $$

    (7.28)

• 2. Calculation Stage

  • a. Copy left, right and previous time step (pr) signals (multiple gates operate on each):

    $$Last\mathop {\longrightarrow {}}\limits ^{k_{x}}Last+BrPr $$

    (7.29)
    $$BrPr\mathop {\longrightarrow {}}\limits ^{k_{x}}waste $$

    (7.30)
    $$Rght\mathop {\longrightarrow {}}\limits ^{k_{x}}Rght+RBr $$

    (7.31)
    $$RBr\mathop {\longrightarrow {}}\limits ^{k_{x}}waste $$

    (7.32)
    $$Last\mathop {\longrightarrow {}}\limits ^{k_{x}}Last+OnPr $$

    (7.33)
    $$OnPr\mathop {\longrightarrow {}}\limits ^{k_{x}}waste $$

    (7.34)
    $$Rght\mathop {\longrightarrow {}}\limits ^{k_{x}}Rght+RCr $$

    (7.35)
    $$RCr\mathop {\longrightarrow {}}\limits ^{k_{x}}waste $$

    (7.36)
    $$Lft\mathop {\longrightarrow {}}\limits ^{k_{x}}Lft+LCr $$

    (7.37)
    $$LCr\mathop {\longrightarrow {}}\limits ^{k_{x}}waste $$

    (7.38)
    $$source\mathop {\longrightarrow {}}\limits ^{k_{p}}OffPr $$

    (7.39)
    $$OffPr\mathop {\longrightarrow {}}\limits ^{k_{x}}waste $$

    (7.40)
    $$BrPr+OffPr\mathop {\longrightarrow {}}\limits ^{k_{T}}waste $$

    (7.41)

  • a. Boolean logic for Br (birth) condition: off to on transition:

    $$source\mathop {\longrightarrow {}}\limits ^{2*k_{p}}SgBr\mathop {\longrightarrow {}}\limits ^{k_{x}}waste $$

    (7.42)
    $$OffPr+SgBr\mathop {\longrightarrow {}}\limits ^{k_{L}}SumBr\mathop {\longrightarrow {}}\limits ^{k_{x}}waste $$

    (7.43)
    $$RBr+SgBr\mathop {\longrightarrow {}}\limits ^{k_{L}}SumBr $$

    (7.44)
    $$source\mathop {\longrightarrow {}}\limits ^{1.35*k_{p}}ThBr\mathop {\longrightarrow {}}\limits ^{k_{x}}waste $$

    (7.45)
    $$source\mathop {\longrightarrow {}}\limits ^{k_{p}}AmpBr\mathop {\longrightarrow {}}\limits ^{k_{x}}waste $$

    (7.46)
    $$SumBr+ThBr\mathop {\longrightarrow {}}\limits ^{k_{T}}waste $$

    (7.47)
    $$SumBr+AmpBr\mathop {\longrightarrow {}}\limits ^{k_{L}}SumBr+Br $$

    (7.48)
    $$Br\mathop {\longrightarrow {}}\limits ^{k_{x}}waste $$

    (7.49)

  • a. Boolean logic for no death condition (on and at least one neighbor off): stay on:

    $$source\mathop {\longrightarrow {}}\limits ^{2*k_{p}}SgnbOff\mathop {\longrightarrow {}}\limits ^{k_{x}}waste $$

    (7.50)
    $$RCr+SgnbOff\mathop {\longrightarrow {}}\limits ^{k_{L}}SumnbOff\mathop {\longrightarrow {}}\limits ^{k_{x}}waste $$

    (7.51)
    $$LCr+SgnbOff\mathop {\longrightarrow {}}\limits ^{k_{L}}SumnbOff $$

    (7.52)
    $$source\mathop {\longrightarrow {}}\limits ^{1.35*k_{p}}ThnbOff\mathop {\longrightarrow {}}\limits ^{k_{x}}waste $$

    (7.53)
    $$source\mathop {\longrightarrow {}}\limits ^{k_{p}}AmpnbOff\mathop {\longrightarrow {}}\limits ^{k_{x}}waste $$

    (7.54)
    $$SumnbOff+ThnbOff\mathop {\longrightarrow {}}\limits ^{k_{T}}waste $$

    (7.55)
    $$ThnbOff+AmpnbOff\mathop {\longrightarrow {}}\limits ^{k_{L}}ThnbOff+nbrOff $$

    (7.56)
    $$nbrOff\mathop {\longrightarrow {}}\limits ^{k_{x}}waste $$

    (7.57)
    $$source\mathop {\longrightarrow {}}\limits ^{2*k_{p}}SgCr\mathop {\longrightarrow {}}\limits ^{k_{x}}waste $$

    (7.58)
    $$OnPr+SgCr\mathop {\longrightarrow {}}\limits ^{k_{L}}SumCr\mathop {\longrightarrow {}}\limits ^{k_{x}}waste $$

    (7.59)
    $$nbrOff+SgCr\mathop {\longrightarrow {}}\limits ^{k_{L}}SumCr $$

    (7.60)
    $$source\mathop {\longrightarrow {}}\limits ^{1.35*k_{p}}ThCr\mathop {\longrightarrow {}}\limits ^{k_{x}}waste $$

    (7.61)
    $$source\mathop {\longrightarrow {}}\limits ^{k_{p}}AmpCr\mathop {\longrightarrow {}}\limits ^{k_{x}}waste $$

    (7.62)
    $$SumCr+ThCr\mathop {\longrightarrow {}}\limits ^{k_{T}}waste $$

    (7.63)
    $$SumCr+AmpCr\mathop {\longrightarrow {}}\limits ^{k_{L}}SumCr+Live $$

    (7.64)
    $$Live\mathop {\longrightarrow {}}\limits ^{k_{x}}waste $$

    (7.65)

  • a. Boolean logic to determine if next state is on:

    $$source\mathop {\longrightarrow {}}\limits ^{2*k_{p}}SgNx\mathop {\longrightarrow {}}\limits ^{k_{x}}waste $$

    (7.66)
    $$Live+SgNx\mathop {\rightarrow {}}\limits ^{k_{L}}SumNx\mathop {\rightarrow {}}\limits ^{k_{x}}waste $$

    (7.67)
    $$Br+SgNx\mathop {\rightarrow {}}\limits ^{k_{L}}SumNx $$

    (7.68)
    $$source\mathop {\longrightarrow {}}\limits ^{0.65*k_{p}}ThNx\mathop {\rightarrow {}}\limits ^{k_{x}}waste $$

    (7.69)
    $$source\mathop {\rightarrow {}}\limits ^{k_{p}}AmpNx\mathop {\rightarrow {}}\limits ^{k_{x}}waste $$

    (7.70)
    $$SumNx+ThNx\mathop {\rightarrow {}}\limits ^{k_{T}}waste $$

    (7.71)
    $$SumNx+AmpNx\mathop {\rightarrow {}}\limits ^{k_{L}}SumNx+Nx $$

    (7.72)
    $$Nx\mathop {\rightarrow {}}\limits ^{k_{x}}waste $$

    (7.73)
    $$Nx\mathop {\rightarrow {}}\limits ^{k_{x}}Nx+OnNx $$

    (7.74)
    $$OnNx\mathop {\rightarrow {}}\limits ^{k_{x}}waste $$

    (7.75)

  • a. Boolean logic to determine if next state is off:

    $$Nx\mathop {\rightarrow {}}\limits ^{k_{x}}Nx+NtNx $$

    (7.76)
    $$NtNx\mathop {\rightarrow {}}\limits ^{k_{x}}waste $$

    (7.77)
    $$source\mathop {\rightarrow {}}\limits ^{k_{p}}OffNx\mathop {\rightarrow {}}\limits ^{k_{x}}waste $$

    (7.78)
    $$NtNx+OffNx\mathop {\rightarrow {}}\limits ^{k_{T}}waste $$

    (7.79)

  • a. Clocked synchronization gates:

    $$clk\mathop {\rightarrow {}}\limits ^{k_{x}}clk+clkOn $$

    (7.80)
    $$clkOn\mathop {\rightarrow {}}\limits ^{k_{x}}waste $$

    (7.81)
    $$clk\mathop {\rightarrow {}}\limits ^{k_{x}}clk+clkOff $$

    (7.82)
    $$clkOff\mathop {\rightarrow {}}\limits ^{k_{x}}waste $$

    (7.83)
    $$source\mathop {\longrightarrow {}}\limits ^{2*k_{p}}SgNxOn\mathop {\rightarrow {}}\limits ^{k_{x}}waste $$

    (7.84)
    $$OnNx+SgNxOn\mathop {\rightarrow {}}\limits ^{k_{L}}OnNxSum\mathop {\rightarrow {}}\limits ^{k_{x}}waste $$

    (7.85)
    $$clkOn+SgNxOn\mathop {\rightarrow {}}\limits ^{k_{L}}OnNxSum $$

    (7.86)
    $$source\mathop {\longrightarrow {}}\limits ^{1.35*k_{p}}OnNxTh\mathop {\rightarrow {}}\limits ^{k_{x}}waste $$

    (7.87)
    $$source\mathop {\rightarrow {}}\limits ^{k_{p}}OnNxAmp\mathop {\rightarrow {}}\limits ^{k_{x}}waste $$

    (7.88)
    $$OnNxSum+OnNxTh\mathop {\rightarrow {}}\limits ^{k_{T}}waste $$

    (7.89)
    $$OnNxSum+OnNxAmp\mathop {\rightarrow {}}\limits ^{k_{L}}OnNxSum+SetBfr $$

    (7.90)
    $$SetBfr\mathop {\rightarrow {}}\limits ^{k_{x}}waste $$

    (7.91)
    $$source\mathop {\longrightarrow {}}\limits ^{2*k_{p}}SgOffNx\mathop {\rightarrow {}}\limits ^{k_{x}}waste $$

    (7.92)
    $$OffNx+SgOffNx\mathop {\rightarrow {}}\limits ^{k_{L}}SumOffNx\mathop {\rightarrow {}}\limits ^{k_{x}}waste $$

    (7.93)
    $$clkOff+SgOffNx\mathop {\rightarrow {}}\limits ^{k_{L}}SumOffNx $$

    (7.94)
    $$source\mathop {\longrightarrow {}}\limits ^{1.35*k_{p}}ThOffNx\mathop {\rightarrow {}}\limits ^{k_{x}}waste $$

    (7.95)
    $$source\mathop {\rightarrow {}}\limits ^{k_{p}}AmpOffNx\mathop {\rightarrow {}}\limits ^{k_{x}}waste $$

    (7.96)
    $$SumOffNx+ThOffNx\mathop {\rightarrow {}}\limits ^{k_{T}}waste $$

    (7.97)
    $$SumOffNx+AmpOffNx\mathop {\rightarrow {}}\limits ^{k_{L}}SumOffNx+ResBfr $$

    (7.98)
    $$ResBfr\mathop {\rightarrow {}}\limits ^{k_{x}}waste $$

    (7.99)

• 3. Storage Stage

  • a. Copies of Set/Res signals:

    $$SetBfr\mathop {\rightarrow {}}\limits ^{k_{x}}SetBfr+Set $$

    (7.100)
    $$Set\mathop {\rightarrow {}}\limits ^{k_{x}}waste $$

    (7.101)
    $$ResBfr\mathop {\rightarrow {}}\limits ^{k_{x}}ResBfr+Res $$

    (7.102)
    $$Res\mathop {\rightarrow {}}\limits ^{k_{x}}waste $$

    (7.103)

  • a. Flip-flop module:

    $$ffBfrd\mathop {\rightarrow {}}\limits ^{k_{x}}ffBfrd+ffFback $$

    (7.104)
    $$ffFback\mathop {\rightarrow {}}\limits ^{k_{x}}waste $$

    (7.105)
    $$source\mathop {\longrightarrow {}}\limits ^{2*k_{p}}N1Sg\mathop {\rightarrow {}}\limits ^{k_{x}}waste $$

    (7.106)
    $$Set+N1Sg\mathop {\rightarrow {}}\limits ^{k_{L}}N1Sum\mathop {\rightarrow {}}\limits ^{k_{x}}waste $$

    (7.107)
    $$ffFback+N1Sg\mathop {\rightarrow {}}\limits ^{k_{L}}N1Sum $$

    (7.108)
    $$source\mathop {\longrightarrow {}}\limits ^{0.65*k_{p}}N1Th\mathop {\rightarrow {}}\limits ^{k_{x}}waste $$

    (7.109)
    $$source\mathop {\rightarrow {}}\limits ^{k_{p}}N1\mathop {\rightarrow {}}\limits ^{k_{x}}waste $$

    (7.110)
    $$N1Sum+N1Th\mathop {\rightarrow {}}\limits ^{k_{T}}waste $$

    (7.111)
    $$N1Th+N1\mathop {\rightarrow {}}\limits ^{k_{L}}N1Th+ffFbackNot $$

    (7.112)
    $$ffFbackNot\mathop {\rightarrow {}}\limits ^{k_{x}}waste $$

    (7.113)
    $$source\mathop {\longrightarrow {}}\limits ^{2*k_{p}}N2Sg\mathop {\rightarrow {}}\limits ^{k_{x}}waste $$

    (7.114)
    $$Res+N2Sg\mathop {\rightarrow {}}\limits ^{k_{L}}N2Sum\mathop {\rightarrow {}}\limits ^{k_{x}}waste $$

    (7.115)
    $$ffFbackNot+N2Sg\mathop {\rightarrow {}}\limits ^{k_{L}}N2Sum $$

    (7.116)
    $$source\mathop {\longrightarrow {}}\limits ^{0.65*k_{p}}N2Th\mathop {\rightarrow {}}\limits ^{k_{x}}waste $$

    (7.117)
    $$source\mathop {\rightarrow {}}\limits ^{k_{p}}N2\mathop {\rightarrow {}}\limits ^{k_{x}}waste $$

    (7.118)
    $$N2Sum+N2Th\mathop {\rightarrow {}}\limits ^{k_{T}}waste $$

    (7.119)
    $$N2Th+N2\mathop {\rightarrow {}}\limits ^{k_{L}}N2Th+ffBfrd $$

    (7.120)
    $$ffBfrd\mathop {\rightarrow {}}\limits ^{k_{x}}waste $$

    (7.121)
    $$ffBfrd\mathop {\rightarrow {}}\limits ^{k_{x}}ffBfrd+Last $$

    (7.122)
    $$Last\mathop {\rightarrow {}}\limits ^{k_{x}}waste $$

    (7.123)

Rule 110 partial differential equations

“I hope to say something about a ‘continuous’ rather than ‘crystalline’ model [of automata]. There, as far as I can now see, a system of nonlinear partial differential equations, essentially of the diffusion type, will be used.” John von Neumann (Oct. 28th, 1952) discussing unfinished Theory of Automata.

von Neumann papers, Library of Congress, Box 28 “Theory of Automata”.

This section describes the set of coupled partial differential equations that govern our Rule 110 chemical automaton, derived from the reactions in this section. These equations use standard mass-action equations and the diffusion equation. Figure 9b contains a plot of the solution to these equations. One equation is devoted to each of the 76 species in our network. Figure 10 shows a detail of the circuit from Fig. 7 for a Rule 110 automaton, with each species labeled.

Unless otherwise specified, all species start with zero initial concentration. Absorbing boundary conditions apply to all species whose concentrations change over time. Our reaction rate constants and diffusion coefficients are selected to be realistically attainable values for DNA-based reaction–diffusion networks, on the same order of magnitude as experimentally derived data in the literature (Zhang and Winfree 2009; Lukacs et al. 2000; Stellwagen et al. 2003). The Mathematica code we used to numerically solve these equations is available upon request. Constants:

$$\begin{aligned} \begin{array}{lll} xMax=64 &{} \qquad \qquad k_{p}=0.002\;\upmu {}\text {M}\,\text{s}^{-1} &{} \qquad \qquad k_{Bd}=0.00002\,\text{s}^{-1}\\ D=0.00015\;\text {mm}^{2}\,\text{s}^{-1} &{} \qquad \qquad k_{d}=0.002\;\upmu {}\,\text {s}^{-1} &{} \qquad \qquad c_{recTh}=0.5\;\upmu {}\text {M}\\ k_{T}=20\;\upmu {}\text {M}^{-1}\,\text {s}^{-1} &{} \qquad \qquad k_{x}=0.002\;\upmu {}\text {M}^{-1}\,\text {s}^{-1} &{} \qquad \qquad clkPeriod = 2*24*3600\;\text {s}\\ k_{L}=0.2\;\upmu {}\text {M}^{-1}\,\text {s}^{-1} &{} \qquad \qquad k_{B}=0.0002\;\upmu {}\text {M}^{-2}\,\text{s}^{-1} &{} \qquad \qquad clkDuty = .5*3600\;\text {s} \end{array} \end{aligned}$$

• 1. External signals:

  • a. Keys (in $\upmu$M):

    $$\begin{aligned} Key_A(t,x)=\,\left\{ \begin{array}{ll}1/(1 + Exp[-25*(Mod(x,16) - 1)]) &{} : Mod(x,16) \le 2\\ 1 - 1/(1 + Exp[-25*(Mod(x,16) - 3)]) &{} : otherwise.\end{array}\right. \end{aligned}$$

    (8.1)
    $$\begin{aligned} Key_B(t,x)=\,\left\{ \begin{array}{ll}1/(1 + Exp[-25*(Mod(x,16) - 5)]) &{} : Mod(x,16) \le 6\\ 1 - 1/(1 + Exp[-25*(Mod(x,16) - 7)]) &{} : otherwise.\end{array}\right. \end{aligned}$$

    (8.2)
    $$\begin{aligned} Key_C(t,x)=\,\left\{ \begin{array}{ll}1/(1 + Exp[-25(Mod(x,16) - 9)]) &{} : mod(x,16) \le 10\\ 1 - 1/(1 + Exp[-25(Mod(x,16) - 11)]) &{} : otherwise.\end{array}\right. \end{aligned}$$

    (8.3)
    $$\begin{aligned} Key_D(t,x)=\,\left\{ \begin{array}{ll}1/(1 + Exp[-25(Mod(x,16) - 13)]) &{} : mod(x,16) \le 14\\ 1 - 1/(1 + Exp[-25(Mod(x,16) - 15)]) &{} : otherwise.\end{array}\right. \end{aligned}$$

    (8.4)

  • b. Clock:

    $$\begin{aligned} clk(t,x)= & {} \left\{ \begin{array}{ll}1 \;\upmu {}\text {M} &{} : t < 4000\\ 1 \;\upmu {}\text {M} &{} : Mod(t, clkPeriod) < clkDuty\\ 0 &{} : otherwise. \end{array}\right. \end{aligned}$$

    (8.5)
    $$\begin{aligned} \frac{\partial {}clk_{On}(t,x)}{\partial {}t}=\, & {} D \nabla {}^2clk_{On}(t,x)-k_{d}*clk_{On}(t,x)+k_{d}*clk(t,x) -k_{L}*clk_{On}(t,x)*Sg_{nxOn}(t,x) \end{aligned}$$

    (8.6)
    $$\begin{aligned} \frac{\partial {}clk_{Off}(t,x)}{\partial {}t}= & {} D\nabla {}^2clk_{Off}(t,x) -k_{d}*clk_{Off}(t,x)+k_{d}*clk(t,x)-k_{L}*clk_{Off} (t,x)*Sg_{OffNx}(t,x) \end{aligned}$$

    (8.7)

• 2. Communication Stage:

  • a. Broadcast Modules (in $\mu$M):

    $$\begin{aligned} Src_A(t,x)= 1 \end{aligned}$$

    (8.8)
    $$\begin{aligned} Src_B(t,x)= 1 \end{aligned}$$

    (8.9)
    $$\begin{aligned} Src_C(t,x)= 1 \end{aligned}$$

    (8.10)
    $$\begin{aligned} Src_D(t,x)= 1 \end{aligned}$$

    (8.11)

  • b. Broadcast signals, note initial concentration of $Sig_A$ triggers initial on cell:

    $$\begin{aligned} \frac{\partial {}Sig_A(t,x)}{\partial {}t}=\, & {} D\nabla {}^2Sig_A(t,x) +k_{B}Src_A(t,x)Key_A(t,x)Last(t,x)-k_{Bd}Sig_A(t,x)\nonumber \\ Sig_A(t=0,x)= & {} \left\{ \begin{array}{ll}2 \;\upmu {}\text {M} &{} : x_{max}-8<x<x_{max}-0.1\\ 0 &{} \quad: otherwise.\end{array}\right. \end{aligned}$$

    (8.12)
    $$\begin{aligned} \frac{\partial {}Sig_B(t,x)}{\partial {}t}= & {} D\nabla {}^2Sig_B(t,x) +k_{B}Src_B(t,x)Key_B(t,x)Last(t,x)-k_{Bd}Sig_B(t,x) \end{aligned}$$

    (8.13)
    $$\begin{aligned} \frac{\partial {}Sig_C(t,x)}{\partial {}t}=\, & {} D\nabla {}^2Sig_C(t,x) +k_{B}Src_C(t,x)Key_C(t,x)Last(t,x)-k_{Bd}Sig_C(t,x) \end{aligned}$$

    (8.14)
    $$\begin{aligned} \frac{\partial {}Sig_D(t,x)}{\partial {}t}= & {} D\nabla {}^2Sig_D(t,x) +k_{B}Src_D(t,x)Key_D(t,x)Last(t,x)-k_{Bd}Sig_D(t,x) \end{aligned}$$

    (8.15)

  • c. Receiving and processing left-hand neighbor signal:

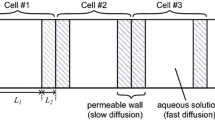
    $$\begin{aligned} \frac{\partial {}L_{raw}(t,x)}{\partial {}t}= & {} D\nabla {}^2L_{raw}(t,x) -4k_{d}L_{raw}(t,x)-k_{T}L_{raw}(t,x)Th_l(t,x) +k_{x}Sig_D(t,x)Key_A(t,x)\nonumber \\&+k_{x}Sig_A(t,x)Key_B(t,x) +k_{x}Sig_B(t,x)Key_C(t,x)+k_{x}Sig_C(t,x)Key_D(t,x) \end{aligned}$$

    (8.16)
    $$\begin{aligned} \frac{\partial {}Th_l(t,x)}{\partial {}t}= & {} D\nabla {}^2Th_l(t,x)+c_{recTh}k_{p}-k_{d}Th_l(t,x)-k_{T}L_{raw}(t,x)Th_l(t,x) \end{aligned}$$

    (8.17)
    $$\begin{aligned} \frac{\partial {}Amp_l(t,x)}{\partial {}t}= & {} D\nabla {}^2Amp_l(t,x)+k_{p}-k_{d}Amp_l(t,x)-k_{L}L_{raw}(t,x)Amp_l(t,x) \end{aligned}$$

    (8.18)
    $$\begin{aligned} \frac{\partial {}Lft(t,x)}{\partial {}t}= & {} D\nabla {}^2Lft(t,x)-k_{d}Lft(t,x)+k_{L}L_{raw}(t,x)Amp_l(t,x) \end{aligned}$$

    (8.19)

  • d. Receiving and processing right-hand neighbor signal:

    $$\begin{aligned} \frac{\partial {}R_{raw}(t,x)}{\partial {}t}= & {} D\nabla {}^2R_{raw}(t,x) -4k_{d}R_{raw}(t,x)-k_{T}R_{raw}(t,x)Th_r(t,x)+k_{x}Sig_(t,x)Key_A(t,x)\nonumber \\&+k_{x}Sig_C(t,x)Key_B(t,x) +k_{x}Sig_D(t,x)Key_C(t,x)+k_{x}Sig_A(t,x)Key_D(t,x) \end{aligned}$$

    (8.20)
    $$\begin{aligned} \frac{\partial {}Th_r(t,x)}{\partial {}t}= & {} D\nabla {}^2Th_r(t,x)+c_{recTh}k_{p}-k_{d}Th_r(t,x)-k_{T}R_{raw}(t,x)Th_r(t,x) \end{aligned}$$

    (8.21)
    $$\begin{aligned} \frac{\partial {}Amp_{rt}(t,x)}{\partial {}t}= & {} D\nabla {}^2Amp_{rt}(t,x)+k_{p}-k_{d}Amp_{rt}(t,x)-k_{L}R_{raw}(t,x)Amp_{rt}(t,x) \end{aligned}$$

    (8.22)
    $$\begin{aligned} \frac{\partial {}Rght(t,x)}{\partial {}t}= & {} D\nabla {}^2Rght(t,x)-k_{d}Rght(t,x)+k_{L}R_{raw}(t,x)Amp_{rt}(t,x) \end{aligned}$$

    (8.23)

• 3. Calculation Stage:

  • a. Copy left, right and previous time step (pr) signals (multiple gates operate on each)

    $$\frac{\partial {}Br_{pr}(t,x)}{\partial {}t}=\,D\nabla {}^2Br_{pr}(t,x)-k_{d}Br_{pr}(t,x)+k_{d}Last(t,x)-k_{T}Br_{pr}(t,x)Off_{pr}(t,x) $$

    (8.24)
    $$\frac{\partial {}R_{br}(t,x)}{\partial {}t}=\,D\nabla {}^2R_{br}(t,x)-k_{d}R_{br}(t,x)+k_{d}Rght(t,x)-k_{L}R_{br}(t,x)Sg_{br}(t,x) $$

    (8.25)
    $$\frac{\partial {}On_{pr}(t,x)}{\partial {}t}=\,D\nabla {}^2On_{pr}(t,x)-k_{d}On_{pr}(t,x)+k_{d}Last(t,x)-k_{L}On_{pr}(t,x)Sg_{cr}(t,x) $$

    (8.26)
    $$\frac{\partial {}R_{cr}(t,x)}{\partial {}t}=\,D\nabla {}^2R_{cr}(t,x)-k_{d}R_{cr}(t,x)+k_{d}Rght(t,x)-k_{L}R_{cr}(t,x)Sg_{nbOff}(t,x) $$

    (8.27)
    $$\frac{\partial {}L_{cr}(t,x)}{\partial {}t}=\,D\nabla {}^2L_{cr}(t,x)-k_{d}L_{cr}(t,x)+k_{d}Lft(t,x)-k_{L}L_{cr}(t,x)Sg_{nbOff}(t,x) $$

    (8.28)
    $$\frac{\partial {}Off_{pr}(t,x)}{\partial {}t}=\,D\nabla {}^2Off_{pr}(t,x)+k_{p}-k_{d}Off_{pr}(t,x)-_{T}Br_{pr}(t,x)Off_{pr}(t,x)-k_{L}Off_{pr}(t,x)Sg_{br}(t,x) $$

    (8.29)

  • b. Boolean logic for Br (birth) condition: off to on transition

    $$\frac{\partial {}Sg_{br}(t,x)}{\partial {}t}=\,D\nabla {}^2Sg_{br}(t,x)+2k_{p}-k_{d}Sg_{br}(t,x)-k_{L}Off_{pr}(t,x)Sg_{br}(t,x)-k_{L}R_{br}(t,x)Sg_{br}(t,x) $$

    (8.30)
    $$\begin{aligned}&\frac{\partial {}Sum_{br}(t,x)}{\partial {}t}=\,D\nabla {}^2Sum_{br}(t,x)-k_{d}Sum_{br}(t,x)+k_{L}Off_{pr}(t,x)Sg_{br}(t,x) +k_{L}R_{br}(t,x)Sg_{br}(t,x)-k_{T}Sum_{br}(t,x)Th_{br}(t,x) \end{aligned}$$

    (8.31)
    $$\begin{aligned}&\frac{\partial {}Th_{br}(t,x)}{\partial {}t}=\,D\nabla {}^2Th_{br}(t,x)+1.35k_{p}-k_{d}Th_{br}(t,x)-k_{T}Sum_{br}(t,x)Th_{br}(t,x) \end{aligned}$$

    (8.32)
    $$\begin{aligned}&\frac{\partial {}Amp_{br}(t,x)}{\partial {}t}=\,D\nabla {}^2Amp_{br}(t,x)+k_{p}-k_{d}Amp_{br}(t,x)-k_{L}Sum_{br}(t,x)Amp_{br}(t,x) \end{aligned}$$

    (8.33)
    $$\begin{aligned}&\frac{\partial {}Br(t,x)}{\partial {}t}=\,D\nabla {}^2Br(t,x)-k_{d}Br(t,x)+k_{L}Sum_{br}(t,x)Amp_{br}(t,x)-k_{L}Br(t,x)Sg_{nx}(t,x) \end{aligned}$$

    (8.34)

  • c. Boolean logic for no death condition (on and at least one neighbor off): stay on

    $$\begin{aligned}&\frac{\partial {}Sg_{nbOff}(t,x)}{\partial {}t}=\,D\nabla {}^2Sg_{nbOff}(t,x)+2k_{p}-k_{d}Sg_{nbOff}(t,x)-k_{L}R_{cr}(t,x)Sg_{nbOff}(t,x)-k_{L}L_{cr}(t,x)Sg_{nbOff}(t,x) \end{aligned}$$

    (8.35)
    $$\begin{aligned}&\frac{\partial {}Sum_{nbOff}(t,x)}{\partial {}t}=\,D\nabla {}^2Sum_{nbOff}(t,x)-k_{d}Sum_{nbOff}(t,x)+k_{L}R_{cr}(t,x)Sg_{nbOff}(t,x)+k_{L}L_{cr}(t,x)Sg_{nbOff}(t,x)-k_{T}Sum_{nbOff}(t,x)Th_{nbOff}(t,x) \end{aligned}$$

    (8.36)
    $$\begin{aligned}&\frac{\partial {}Th_{nbOff}(t,x)}{\partial {}t}=\,D\nabla {}^2Th_{nbOff}(t,x)+1.35k_{p}-k_{d}Th_{nbOff}(t,x)-k_{T}Sum_{nbOff}(t,x)Th_{nbOff}(t,x) \end{aligned}$$

    (8.37)
    $$\begin{aligned}&\frac{\partial {}Amp_{nbOff}(t,x)}{\partial {}t}=\,D\nabla {}^2Amp_{nbOff}(t,x)+k_{p}-k_{d}Amp_{nbOff}(t,x)-k_{L}Th_{nbOff}(t,x)Amp_{nbOff}(t,x) \end{aligned}$$

    (8.38)
    $$\begin{aligned}&\frac{\partial {}nbrOff(t,x)}{\partial {}t}=\,D\nabla {}^2nbrOff(t,x)-k_{d}nbrOff(t,x)+k_{L}Th_{nbOff}(t,x)Amp_{nbOff}y(t,x)-k_{L}nbrOff(t,x)Sg_{cr}(t,x) \end{aligned}$$

    (8.39)
    $$\begin{aligned}&\frac{\partial {}Sg_{cr}(t,x)}{\partial {}t}=\,D\nabla {}^2Sg_{cr}(t,x)+2k_{p}-k_{d}Sg_{cr}(t,x)-k_{L}On_{pr}(t,x)Sg_{cr}(t,x)-k_{L}nbrOff(t,x)Sg_{cr}(t,x) \end{aligned}$$

    (8.40)
    $$\begin{aligned}&\frac{\partial {}Sum_{cr}(t,x)}{\partial {}t}=\,D\nabla {}^2Sum_{cr}(t,x)-k_{d}Sum_{cr}(t,x)+k_{L}On_{pr}(t,x)Sg_{cr}(t,x)+k_{L}nbrOff(t,x)Sg_{cr}(t,x)-k_{T}Sum_{cr}(t,x)Th_{cr}(t,x) \end{aligned}$$

    (8.41)
    $$\begin{aligned}&\frac{\partial {}Th_{cr}(t,x)}{\partial {}t}=\,D\nabla {}^2Th_{cr}(t,x)+1.35k_{p}-k_{d}Th_{cr}(t,x)-k_{T}Sum_{cr}(t,x)Th_{cr}(t,x) \end{aligned}$$

    (8.42)
    $$\begin{aligned}&\frac{\partial {}Amp_{cr}(t,x)}{\partial {}t}=\,D\nabla {}^2Amp_{cr}(t,x)+k_{p}-k_{d}Amp_{cr}(t,x)-k_{L}Sum_{cr}(t,x)Amp_{cr}(t,x) \end{aligned}$$

    (8.43)
    $$\begin{aligned}&\frac{\partial {}Live(t,x)}{\partial {}t}=\,D\nabla {}^2Live(t,x)-k_{d}Live(t,x)+k_{L}Sum_{cr}(t,x)Amp_{cr}(t,x)-k_{L}Live(t,x)Sg_{nx}(t,x) \end{aligned}$$

    (8.44)

  • d. Boolean logic to determine if next state is on

    $$\begin{aligned}&\frac{\partial {}Sg_{nx}(t,x)}{\partial {}t}=\,D\nabla {}^2Sg_{nx}(t,x)+2k_{p}-k_{d}Sg_{nx}(t,x)-k_{L}Live(t,x)Sg_{nx}(t,x)-k_{L}Br(t,x)Sg_{nx}(t,x) \end{aligned}$$

    (8.45)
    $$\begin{aligned}&\frac{\partial {}Sum_{nx}(t,x)}{\partial {}t}=\,D\nabla {}^2Sum_{nx}(t,x)-k_{d}Sum_{nx}(t,x)+k_{L}Live(t,x)Sg_{nx}(t,x)+k_{L}Br(t,x)Sg_{nx}(t,x)-k_{T}Sum_{nx}(t,x)Th_{nx}(t,x) \end{aligned}$$

    (8.46)
    $$\begin{aligned}&\frac{\partial {}Th_{nx}(t,x)}{\partial {}t}=\,D\nabla {}^2Th_{nx}(t,x)+0.65k_{p}-k_{d}Th_{nx}(t,x)-k_{T}Sum_{nx}(t,x)Th_{nx}(t,x) \end{aligned}$$

    (8.47)
    $$\begin{aligned}&\frac{\partial {}Amp_{nx}(t,x)}{\partial {}t}=\,D\nabla {}^2Amp_{nx}(t,x)+k_{p}-k_{d}Amp_{nx}(t,x)-k_{L}Sum_{nx}(t,x)Amp_{nx}(t,x) \end{aligned}$$

    (8.48)
    $$\begin{aligned}&\frac{\partial {}Nx(t,x)}{\partial {}t}=\,D\nabla {}^2Nx(t,x)-k_{d}Nx(t,x)+k_{L}Sum_{nx}(t,x)Amp_{nx}(t,x) \end{aligned}$$

    (8.49)
    $$\begin{aligned}&\frac{\partial {}On_{nx}(t,x)}{\partial {}t}=\,D\nabla {}^2On_{nx}(t,x)-k_{d}On_{nx}(t,x)+k_{d}Nx(t,x)-k_{L}On_{nx}(t,x)Sg_{nxOn}(t,x) \end{aligned}$$

    (8.50)

  • e. Boolean logic to determine if next state is off

    $$\begin{aligned}&\frac{\partial {}Nt_{nx}(t,x)}{\partial {}t}=\,D\nabla {}^2Nt_{nx}(t,x)-k_{d}Nt_{nx}(t,x)+k_{d}Nx(t,x)-k_{T}Nt_{nx}(t,x)Off_{nx}(t,x) \end{aligned}$$

    (8.51)
    $$\begin{aligned}&\frac{\partial {}Off_{nx}(t,x)}{\partial {}t}=\,D\nabla {}^2Off_{nx}(t,x)+k_{p}-k_{d}Off_{nx}(t,x)-k_{T}Nt_{nx}(t,x)Off_{nx}(t,x)-k_{L}Off_{nx}(t,x)Sg_{OffNx}(t,x) \end{aligned}$$

    (8.52)

  • f. Clocked synchronization gates

    $$\begin{aligned}&\frac{\partial {}Sg_{nxOn}(t,x)}{\partial {}t}=\,D\nabla {}^2Sg_{nxOn}(t,x)+2k_{p}-k_{d}Sg_{nxOn}(t,x)-k_{L}On_{nx}(t,x)Sg_{nxOn}(t,x)-k_{L}clk_{On}(t,x)Sg_{nxOn}(t,x) \end{aligned}$$

    (8.53)
    $$\begin{aligned}&\frac{\partial {}On_{nx}Sum(t,x)}{\partial {}t}=\,D\nabla {}^2On_{nx}Sum(t,x)-k_{d}On_{nx}Sum(t,x)+k_{L}On_{nx}(t,x)Sg_{nxOn}(t,x)+k_{L}clk_{On}(t,x)Sg_{nxOn}(t,x)-k_{T}On_{nx}Sum(t,x)On_{nx}Th(t,x) \end{aligned}$$

    (8.54)
    $$\begin{aligned}&\frac{\partial {}On_{nx}Th(t,x)}{\partial {}t}=\,D\nabla {}^2On_{nx}Th(t,x)+1.35k_{p}-k_{d}On_{nx}Th(t,x)-k_{T}On_{nx}Sum(t,x)On_{nx}Th(t,x) \end{aligned}$$

    (8.55)
    $$\begin{aligned}&\frac{\partial {}On_{nx}Amp(t,x)}{\partial {}t}=\,D\nabla {}^2On_{nx}Amp(t,x)+k_{p}-k_{d}On_{nx}Amp(t,x)-k_{L}On_{nx}Sum(t,x)On_{nx}Amp(t,x) \end{aligned}$$

    (8.56)
    $$\begin{aligned}&\frac{\partial {}Set_{Bfr}(t,x)}{\partial {}t}=\,D\nabla {}^2Set_{Bfr}(t,x)-k_{d}Set_{Bfr}(t,x)+k_{L}On_{nx}Sum(t,x)On_{nx}Amp(t,x) \end{aligned}$$

    (8.57)
    $$\begin{aligned}&\frac{\partial {}Sg_{OffNx}(t,x)}{\partial {}t}=\,D\nabla {}^2Sg_{OffNx}(t,x)+2k_{p}-k_{d}Sg_{OffNx}(t,x)-k_{L}Off_{nx}(t,x)Sg_{OffNx}(t,x)-k_{L}clk_{Off}(t,x)Sg_{OffNx}(t,x) \end{aligned}$$

    (8.58)
    $$\begin{aligned}&\frac{\partial {}Sum_{OffNx}(t,x)}{\partial {}t}=\,D\nabla {}^2Sum_{OffNx}(t,x)-k_{d}Sum_{OffNx}(t,x)+k_{L}Off_{nx}(t,x)Sg_{OffNx}(t,x)+k_{L}clk_{Off}(t,x)Sg_{OffNx}(t,x)-k_{T}Sum_{OffNx}(t,x)Th_{OffNx}(t,x) \end{aligned}$$

    (8.59)
    $$\begin{aligned}&\frac{\partial {}Th_{OffNx}(t,x)}{\partial {}t}=\,D\nabla {}^2Th_{OffNx}(t,x)+1.35k_{p}-k_{d}Th_{OffNx}(t,x)-k_{T}Sum_{OffNx}(t,x)Th_{OffNx}(t,x) \end{aligned}$$

    (8.60)
    $$\begin{aligned}&\frac{\partial {}Amp_{OffNx}(t,x)}{\partial {}t}=\,D\nabla {}^2Amp_{OffNx}(t,x)+k_{p}-k_{d}Amp_{OffNx}(t,x)-k_{L}Sum_{OffNx}(t,x)Amp_{OffNx}(t,x) \end{aligned}$$

    (8.61)
    $$\begin{aligned}&\frac{\partial {}Res_{Bfr}(t,x)}{\partial {}t}=\,D\nabla {}^2Res_{Bfr}(t,x)-k_{d}Res_{Bfr}(t,x)+k_{L}Sum_{OffNx}(t,x)Amp_{OffNx}(t,x) \end{aligned}$$

    (8.62)

• 4. Storage stage

  • a. Copies of Set/Res signals

    $$\begin{aligned}&\frac{\partial {}Set(t,x)}{\partial {}t}=\,D\nabla {}^2Set(t,x)-k_{d}Set(t,x)+k_{d}Set_{Bfr}(t,x)-k_{L}Set(t,x)N1Sg(t,x) \end{aligned}$$

    (8.63)
    $$\begin{aligned}&\frac{\partial {}Res(t,x)}{\partial {}t}=\,D\nabla {}^2Res(t,x)-k_{d}Res(t,x)+k_{d}Res_{Bfr}(t,x)-k_{L}Res(t,x)N2Sg(t,x) \end{aligned}$$

    (8.64)

  • b. Flip-flop module

    $$\begin{aligned}&\frac{\partial {}ffBfrd(t,x)}{\partial {}t}=\,D\nabla {}^2ffBfrd(t,x)-k_{d}ffBfrd(t,x)+k_{L}N2Th(t,x)N2(t,x) \end{aligned}$$

    (8.65)
    $$\begin{aligned}&\frac{\partial {}ffFbackNot(t,x)}{\partial {}t}=\,D\nabla {}^2ffFbackNot(t,x)-k_{d}ffFbackNot(t,x)+k_{L}N1Th(t,x)N1(t,x)-k_{L}ffFbackNot(t,x)N2Sg(t,x) \end{aligned}$$

    (8.66)
    $$\begin{aligned}&\frac{\partial {}N1Th(t,x)}{\partial {}t}=\,D\nabla {}^2N1Th(t,x)+0.65k_{p}-k_{d}N1Th(t,x)-k_{T}N1Sum(t,x)N1Th(t,x) \end{aligned}$$

    (8.67)
    $$\begin{aligned}&\frac{\partial {}N2Sum(t,x)}{\partial {}t}=\,D\nabla {}^2N2Sum(t,x)-k_{d}N2Sum(t,x)+k_{L}Res(t,x)N2Sg(t,x)+k_{L}ffFbackNot(t,x)N2Sg(t,x)-k_{T}N2Sum(t,x)N2Th(t,x) \end{aligned}$$

    (8.68)
    $$\begin{aligned}&\frac{\partial {}ffFback(t,x)}{\partial {}t}=\,D\nabla {}^2ffFback(t,x)-k_{d}ffFback(t,x)+k_{d}ffBfrd(t,x)-k_{L}ffFback(t,x)N1Sg(t,x) \end{aligned}$$

    (8.69)
    $$\begin{aligned}&\frac{\partial {}N1Sg(t,x)}{\partial {}t}=\,D\nabla {}^2N1Sg(t,x)+2k_{p}-k_{d}N1Sg(t,x)-k_{L}Set(t,x)N1Sg(t,x)-k_{L}ffFback(t,x)N1Sg(t,x) \end{aligned}$$

    (8.70)
    $$\begin{aligned}&\frac{\partial {}N1Sum(t,x)}{\partial {}t}=\,D\nabla {}^2N1Sum(t,x)-k_{d}N1Sum(t,x)+k_{L}Set(t,x)N1Sg(t,x)+k_{L}ffFback(t,x)N1Sg(t,x)-k_{T}N1Sum(t,x)N1Th(t,x) \end{aligned}$$

    (8.71)
    $$\begin{aligned}&\frac{\partial {}N1(t,x)}{\partial {}t}=\,D\nabla {}^2N1(t,x)+k_{p}-k_{d}N1(t,x)-k_{L}N1Th(t,x)N1(t,x) \end{aligned}$$

    (8.72)
    $$\begin{aligned}&\frac{\partial {}N2Sg(t,x)}{\partial {}t}=\,D\nabla {}^2N2Sg(t,x)+2k_{p}-k_{d}N2Sg(t,x)-k_{L}Res(t,x)N2Sg(t,x)-k_{L}ffFbackNot(t,x)N2Sg(t,x) \end{aligned}$$

    (8.73)
    $$\begin{aligned}&\frac{\partial {}N2Th(t,x)}{\partial {}t}=\,D\nabla {}^2N2Th(t,x)+0.65k_{p}-k_{d}N2Th(t,x)-k_{T}N2Sum(t,x)N2Th(t,x) \end{aligned}$$

    (8.74)
    $$\begin{aligned}&\frac{\partial {}N2(t,x)}{\partial {}t}=\,D\nabla {}^2N2(t,x)+k_{p}-k_{d}N2(t,x)-k_{L}N2Th(t,x)N2(t,x) \end{aligned}$$

    (8.75)

  • c. Stored state

    $$\begin{aligned} \frac{\partial {}Last(t,x)}{\partial {}t}=\,D\nabla {}^2Last(t,x)-k_{d}Last(t,x)+k_{d}ffBfrd(t,x) \end{aligned}$$

    (8.76)