Skip to main content
SpringerLink
Log in

Mixed-order sampling of 2-D frequency distributions by using the concept of common superset

  • Published:
Multidimensional Systems and Signal Processing Aims and scope Submit manuscript

Abstract

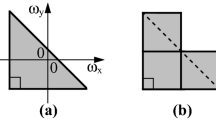
It has been found that tiling clusters and pair regions of frequency distributions play an important role in the sampling problems. When a given 2-D frequency distribution is made up of one tiling cluster, first-order sampling can be used, and when it is made up of two tiling clusters with the same periodicity lattice system, second-order sampling can be used by dividing tiling clusters into sets of pair regions. However, what kind of sampling can be used for other complicated 2-D frequency distributions has not been found. The sampling of frequency distributions which are made up of tiling clusters that belong to different periodicity lattice systems is discussed in this paper. We introduce the concept of common superset as the lattice system which is the common superset of all the lattice systems derived from individual tiling clusters. In practice, the sampling of a 2-D frequency distribution made up of one main body components and two debris ones is calculated in this paper. This type of sampling is a mixture of first-order and higher-order samplings. This sampling method can be applied to other 2-D frequency distributions, when there is a common superset for the given frequency distribution.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14

Similar content being viewed by others

References

  • Bracewell, R. (1965). The Fourier transform and its applications. New York: McGraw-Hill Inc.

    MATH  Google Scholar 

  • Brown, J. L. Jr. (1980). First-order sampling of bandpass signals—A new approach. IEEE Transactions on Information Theory, IT–26(5), 613–614.

  • Coulson, A. J. (1995). A generalization of nonuniform bandpass sampling. IEEE Transactions on Signal Processing, 43(3), 694–704.

    Article  Google Scholar 

  • Ding, F., Qiu, L., & Chen, T. (2009). Reconstruction of continuous-time systems from their non-uniformly sampled discrete-time systems. Automatica, 45(2), 324–332.

    Article  MathSciNet  MATH  Google Scholar 

  • Feldman, C. B., & Bennett, W. R. (1949). Bandwidth and transmission performance. Bell System Technical Journal, 28(3), 490–595.

    Article  Google Scholar 

  • Harish, V., Sommen, P., & Prabhu, K. M. M. (2011). Perfect reconstruction of uniform samples from K-th order nonuniform samples. Signal Processing, 91(11), 2677–2684.

    Article  MATH  Google Scholar 

  • Hori, T. (2014). Novel one-dimensional sampling method to calculate two-dimensional diamond-shaped discrete frequency distributions. IEEE Transactions on Circuits and Systems-II, 61(4), 269–273.

    Article  Google Scholar 

  • Hori, T. (2016). Relationship between Smith normal form of periodicity matrices and sampling of 2-D discrete frequency distributions with tiling capability. IEEE Transactions on Circuits and Systems-II, 63(2), 191–195.

    Article  Google Scholar 

  • Hori, T. (2017). Second-order sampling of 2-D frequency distributions by using the concepts of tiling clusters and pair regions. IEICE Transactions on Fundamentals of Electronics, Communications and Computer Sciences, E100–A(6), 1286–1295.

    Article  Google Scholar 

  • Kohlenberg, A. (1953). Exact interpolation of band-limited functions. Journal of Applied Physics, 24(12), 1432–1436.

    Article  MathSciNet  MATH  Google Scholar 

  • Lin, Y.-P., & Vaidyanathan, P. P. (1996). Theory and design of two-parallelogram filter banks. IEEE Transactions on Signal Processing, 44(11), 2688–2706.

    Article  Google Scholar 

  • Lin, Y.-P., & Vaidyanathan, P. P. (1998). Periodically nonuniform sampling of bandpass signals. IEEE Transactions on Circuits and Systems-II, 45(3), 340–351.

    Article  Google Scholar 

  • Linden, D. A. (1959). A discussion of sampling theorems. Proceedings of the IRE, 47(7), 1219–1226.

    Article  Google Scholar 

  • Marvasti, F. (1996). Nonuniform sampling theorems for bandpass signals at or below the Nyquist density. IEEE Transactions on Signal Processing, 44(3), 572–576.

    Article  Google Scholar 

  • Marvasti, F. (2001). Nonlinear sampling—Theory and Practice (Vol. 1 and 2). New York: Springer.

    MATH  Google Scholar 

  • Petersen, D. P., & Middleton, D. (1962). Sampling and reconstruction of wave-number-limited functions in N-dimensional Euclidean spaces. Information and Control, 5(4), 279–323.

    Article  MathSciNet  Google Scholar 

  • Sindhi, S. K., & Prabhu, K. M. M. (2013). Reconstruction of N-th order nonuniformly sampled bandlimited signals using digital filter banks. Digital Signal Processing, 23(6), 1877–1886.

    Article  Google Scholar 

  • Sommen, P., & Janse, K. (2008). On the relationship between uniform and recurrent nonuniform discrete-time sampling schemes. IEEE Transactions on Signal Processing, 56(10), 5147–5156.

    Article  MathSciNet  MATH  Google Scholar 

  • Tertinek, S., & Vogel, C. (2007). Reconstruction of two-periodic nonuniformly sampled band-limited signals using a discrete-time differentiator and a time-varying multiplier. IEEE Transactions on Circuits and Systems-II, 54(7), 616–620.

    Article  Google Scholar 

  • Tertinek, S., & Vogel, C. (2008). Reconstruction of nonuniformly sampled bandlimited signals using a differentiator–multiplier cascade. IEEE Transactions on Circuits and Systems-I, 55(8), 2273–2286.

    Article  MathSciNet  Google Scholar 

  • Unser, M. (2000). Sampling—50 years after Shannon. Proceedings of the IEEE, 88(4), 569–587.

    Article  MATH  Google Scholar 

  • Vaidyanathan, P. P. (1993). Multirate systems and filter banks. Upper Saddle River, NJ: Prentice Hall Inc.

    MATH  Google Scholar 

  • Vaughan, R. G., Scott, N. L., & White, D. R. (1991). The theory of bandpass sampling. IEEE Transactions on Signal Processing, 39(9), 1973–1984.

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. National Institute of Technology, Tokyo College, 1220-2 Kunugida-cho, Hachioji, Tokyo, 193-0997, Japan

    Toshihiro Hori

Authors
  1. Toshihiro Hori
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Toshihiro Hori.

Additional information

Publisher's Note

Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Hori, T. Mixed-order sampling of 2-D frequency distributions by using the concept of common superset. Multidim Syst Sign Process 30, 1237–1262 (2019). https://doi.org/10.1007/s11045-018-0604-2

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11045-018-0604-2

Keywords

Search

Navigation