Abstract
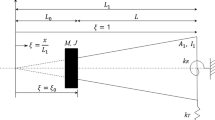
The aim of this paper is to present a method based on a 2D Hopfield Neural Network for online damage detection in beams subjected to external forces. The underlying idea of the method is that a significant change in the beam model parameters can be taken as a sign of damage occurrence in the structural system. In this way, damage detection can be associated to an identification problem. More concretely, a 2D Hopfield Neural Network uses information about the way the beam vibrates and the external forces that are applied to it to obtain time-evolving estimates of the beam parameters at the different beam points. The neural network organizes its input information based on the Euler–Bernoulli model for beam vibrations. Its performance is tested with vibration data generated by means of a different model, namely Timonshenko’s, in order to produce more realistic simulation conditions.




Similar content being viewed by others
References
Almeida, J., Alonso, H., & Rocha, P. (2013). A 2D neural network approach for beam damage detection. In 8th international workshop on multidimensional systems (nDS13), Erlangen, Deutschland.
Almeida, J., Alonso, H., & Rocha, P. (2013). A neural network approach to damage detection in Euler–Bernoulli beams subjected to external forces. In 21st Mediterranean conference on control and automation, Greece.
Alonso, H., Mendonça, T., & Rocha, P. (2009). Hopfield neural networks for online parameter estimation. Neural Networks, 22, 450–462.
Bauchau, O. A., & Craig, J. I. (2009). Structural analysis (solid mechanics and its applications), Vol. 163 (pp. 173–221). Berlin: Springer.
Cao, M., Ye, L., Zhou, L., Zhongqing, S., & Bai, R. (2011). Sensitivity of fundamental mode shape and static deflection for damage identification in cantilever beams. Mechanical Systems and Signal Processing, 25, 630–643.
Erturk, A., & Inman, D. (2011). Piezoelectric energy harvesting. New York: Wiley.
Hladowski, L., Galkowski, K., Cai, Z., Rogers, E., Freeman, C. T., & Lewin, P. L. (2011). A 2D systems approach to iterative learning control for discrete linear processes with zero Markov parameters. International Journal of Control, 84(7), 1246–1262.
Kaneko, T. (1975). On Timoshenko correction for shear in vibrating beams. Journal of Physics D, 8, 1927–1936.
Kim, D.-G., & Lee, S.-B. (2010). Structural damage identification of a cantilever beam using excitation force level control. Mechanical Systems and Signal Processing, 24, 1814–1830.
Ljung, L. (1999). System identification (2nd ed): Theory for the user. Upper Saddle River, NJ: Prentice Hall.
Niemann, H., Morlier, J., Shahdin, A., & Gourinat, Y. (2010). Damage localization using experimental modal parameters and topology optimization. Mechanical Systems and Signal Processing, 24, 636–652.
Radziński, M., Krawczuk, M., & Palacz, M. (2011). Improvement of damage detection methods based on experimental modal parameters. Mechanical Systems and Signal Processing, 25, 2169–2190.
Ribeiro, P. (2012). Vibration of beams in the elasto-plastic and geometrically nonlinear regime, Chapter 5. In Wagg, D., Virgin, L.N. (Eds.), Lecture notes of CISM advanced school exploiting nonlinear behaviour in structural dynamics (pp. 171–223). Wien: Springer.
Ribeiro, P. (2004). A p-version, first order shear deformation, finite element for geometrically non-linear vibration of curved beams. International Journal for Numerical Methods in Engineering, 61, 2696–2715.
Stojanovic, V., Ribeiro, P., & Stoykov, S. (2013). Non-linear vibration of Timoshenko damaged beams by a new p-version finite element method. Computers and Structures, 120, 107–119.
Weaver, W., Timoshenko, S. P., & Young, D. H. (1990). Vibration problems in engineering. New York: Wiley.
Zienkiewicz, O. C., & Morgan, K. (1983). Finite elements and approximation. New York: Wiley-Interscience.
Acknowledgments
This work supported by FEDER founds through COMPETE–Operational Programme Factors of Competitiveness (“Programa Operacional Factores de Competitividade”) and by Portuguese founds through the Portuguese Foundation for Science and Technology (“FCT—Fundação para a Ciência e a Tecnologia”), within the project UID/MAT/04106/2013 associated with the Center for Research and Development in Mathematics and Applications (University of Aveiro), and the project INSTEAD, PTDC/EEA-AUT/108180/2008 with COMPETE reference FCOMP-01-0124-FEDER-009842.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors hereby declare that there are no potential conflicts of interest in this work.
Rights and permissions
About this article
Cite this article
Almeida, J., Alonso, H., Ribeiro, P. et al. A 2D Hopfield Neural Network approach to mechanical beam damage detection. Multidim Syst Sign Process 26, 1081–1095 (2015). https://doi.org/10.1007/s11045-015-0342-7
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11045-015-0342-7