Modelling and stabilization of a load suspended by cable from an airship

Abstract

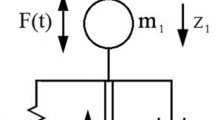
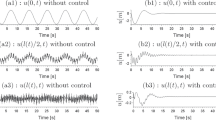
In this paper we present the modeling of an airship with a load suspended by a flexible heavy cable. The objective is to determine a control law that allows to stabilize the machine and its load under the effect of a gust of wind. In order to overcome the great inertia of the airship and the impossibility of using the accelerations of the latter to attenuate the oscillations of the suspended load, a new actuator was proposed at the exit of the cable in order to control its oscillations, namely a motorized cardan joint. The methodology of the study consisted of extracting a reduced dynamic model, which allowed us to build a robust control vector in order to stabilize the suspended load. The analysis of the stability of the zero dynamics of the system was carried out by means of the phase portraits of Poincaré. Numerical simulations were carried out and demonstrated the interest of our approach.

Appendix

The discretized kinetic energy is written as:

$$\begin{aligned} T &= \frac{1}{2}[(\rho L + M_{s} + M_{D})u^{2} + (I_{s} + I_{m} + M_{s}(L + r_{s})^{2} + \rho \frac{L^{3}}{3})q_{1}^{2} \\ &\quad{}+ \delta ^{t}(M_{s}\omega _{L}\omega _{L}^{t} + r_{s}^{2}M_{s}\omega _{z_{2},L}\omega _{z_{2},L}^{t} + \rho \int _{0}^{L} \omega \omega ^{t}dz_{2} - \rho \int _{0}^{L} z_{2}\int _{0}^{z_{2}} \omega _{s}\omega _{s}^{t}dsdz_{2})\delta q_{1}^{2} \\ &\quad{} + (2\rho \int _{0}^{L} \omega ^{t}dz_{2} + 2M_{s}\omega _{L}^{t} + 2M_{s}r_{s}\omega _{z_{2},L}^{t})\dot{\delta} c\theta _{s}u \\ &\quad{} + \delta ^{t}( - 2M_{s}r_{s}\omega _{L}'\omega _{z_{2},L}^{t} - 2M_{s}\int _{0}^{L} \omega _{z_{2}}\omega _{z_{2}}^{t}dz_{2} + 2\rho \int _{0}^{L} \int _{0}^{z_{2}} \omega _{s}\omega _{s}^{t}dsdz_{2})s\theta _{s}u\dot{\delta} \\ &\quad{} + (2I_{s}\omega _{z_{2},L}^{t} + 2M_{s}(L + r_{s})\omega _{L}^{t} + 2M_{s}r_{s}(L + r_{s})\omega _{z_{2},L}^{t} + 2\rho \int _{0}^{L} z_{2}\omega ^{t}dz_{2})\dot{\delta} q_{1} \\ &\quad{} + ((L^{2}\rho + 2M_{s}(L + r_{s}) + \delta ^{t}( - \rho \int _{0}^{L} \int _{0}^{z_{2}} \omega _{s}\omega _{s}^{t}dsdz_{2} - M_{s}r_{s}\omega _{z_{2},L}\omega _{z_{2},L}^{t} \\ &\quad{} - M_{s}\int _{0}^{L} \omega _{z_{2}}\omega _{z_{2}}^{t}ds)\delta )c\theta _{s} + (2\rho \int _{0}^{L} \omega ^{t}dz_{2} - 2M_{s}\omega _{L}^{t} + 2M_{s}r_{s}\omega _{z_{2},L}^{t})\delta s\theta _{s})uq_{1} \\ &\quad{} + \dot{\delta}^{t}(\rho \int _{0}^{L} \omega \omega ^{t}dz_{2} + I_{s}\omega _{z_{2},L}\omega _{z_{2},L}^{t} + M_{s}(\omega _{L}\omega _{L}^{t} + \omega _{z_{2},L}\omega _{z_{2},L}^{t}r_{s}^{2} + 2r_{s}\omega _{L}\omega _{z_{2},L}^{t})\dot{\delta} )] \end{aligned}$$

(72)

To simplify the writing of kinetic energy, the following intermediate quantities are used:

$$\begin{aligned} &A_{1} = \rho L + M_{s} + M_{A} \\ &A_{2} = I_{s} + I_{m} + M_{s}(L + r_{s})^{2} + \rho \frac{L^{3}}{3} \\ &A_{3} = - \rho \int _{0}^{L} z_{2}\int _{0}^{z_{2}} \omega _{z_{2}}\omega _{z_{2}}^{t}dsdz_{2} + \rho \int _{0}^{L} \omega \omega ^{t}dz_{2} + M_{s}\omega _{L}\omega _{L}^{t} + r_{s}^{2}M_{s}\omega _{z_{2},L}\omega _{z_{2},L}^{t} \\ &A_{4} = 2\rho \int _{0}^{L} \omega ^{t}dz_{2} + 2M_{s}\omega _{L}^{t} + 2M_{s}r_{s}\omega _{z_{2},L}^{t} \\ &A_{5} = 2\rho \int _{0}^{L} \int _{0}^{z_{2}} \omega _{z_{2}}\omega _{z_{2}}^{t}dsdz_{2} - 2M_{s}\int _{0}^{L} \omega _{z_{2}}\omega _{z_{2}}^{t}dz_{2} - 2M_{s}r_{s}\omega _{L}'\omega _{z_{2},L}^{t} \\ &A_{6} = 2\rho \int _{0}^{L} z_{2}\omega ^{t}dz_{2} + 2I_{s}\omega _{z_{2},L}^{t} + 2M_{s}(L + r_{s})\omega _{L}^{t} + 2M_{s}r_{s}(L + r_{s})\omega _{z_{2},L}^{t} \\ &A_{7} = L^{2}\rho + 2M_{s}(L + r_{s}) \\ &A_{8} = - \rho \int _{0}^{L} \int _{0}^{z_{2}} \omega _{z_{2}}\omega _{z_{2}}^{t}dsdz_{2} - M_{s}r_{s}\omega _{z_{2},L}\omega _{z_{2},L}^{t} - M_{s}\int _{0}^{L} \omega _{z_{2}}\omega _{z_{2}}^{t}dz_{2} \\ &A_{9} = 2\rho \int _{0}^{L} \omega ^{t}dz_{2} - 2M_{s}\omega _{L}^{t} + 2M_{s}r_{s}\omega _{z_{2},L}^{t} \\ & A_{10} = \rho \int _{0}^{L} \omega \omega ^{t}dz_{2} + I_{s}\omega _{z_{2},L}\omega _{z_{2},L}^{t} + M_{s}(\omega _{L}\omega _{L}^{t} + \omega _{z_{2},L}\omega _{z_{2},L}^{t}r_{s}^{2} + 2r_{s}\omega _{L}\omega _{z_{2},L}^{t}) \end{aligned}$$

(73)

The potential energy is discretized as follows:

$$\begin{aligned} V &= \frac{1}{2}\delta ^{t}EI_{y_{2}}\int _{0}^{L} \omega _{z_{2}z_{2}}\omega _{z_{2}z_{2}}^{t}dz_{2}\delta + g\rho \int _{0}^{L} \omega ^{t}dz_{2}\delta .s\theta _{s} \\ &\quad{} - g\rho .c\theta _{s}(\frac{L^{2}}{2} - \delta ^{t}\frac{1}{2}\int _{0}^{L} \int _{0}^{z_{2}} \omega _{s}\omega _{s}^{t}dsdz_{2}\delta ) + M_{s}g.s\theta _{s}(\omega _{L}^{t}\delta - r_{s}\omega _{z_{2},L}^{t}\delta ) \\ &\quad{} - M_{s}g.c\theta _{s}(L + r_{s} - \delta ^{t}\frac{1}{2}r_{s}\omega _{z_{2},L}\omega _{z_{2},L}^{t}\delta - \delta ^{t}\frac{1}{2}\int _{0}^{L} \omega _{z_{2}}\omega _{z_{2}}^{t}ds\delta ) \\ & = \frac{1}{2}\delta ^{t}EI_{y_{2}}\int _{0}^{L} \omega _{z_{2}z_{2}}\omega _{z_{2}z_{2}}^{t}dz_{2}\delta + ( - \rho \frac{L^{2}}{2} - (L + r_{s})M_{s})g.c\theta _{s} \\ &\quad{}+ \frac{1}{2}\delta ^{t}(\rho \int _{0}^{L} \int _{0}^{z_{2}} \omega _{s}\omega _{s}^{t}dsdz_{2} + M_{s}(\frac{1}{2}r_{s}\omega _{z_{2},L}\omega _{z_{2},L}^{t} + \frac{1}{2}\int _{0}^{L} \omega _{z_{2}}\omega _{z_{2}}^{t}dz_{2}))\delta g.c\theta _{s} \\ &\quad{} + g.s\theta _{s}(\rho \int _{0}^{L} \omega ^{t}dz_{2} + M_{s}(\omega _{L}^{t} - r_{s}\omega _{z_{2},L}^{t}))\delta \end{aligned}$$

(74)

with:

$$ K_{ff} = EI_{y_{2}}\int _{0}^{L} \omega _{z_{2}z_{2}}\omega _{z_{2}z_{2}}^{t}dz_{2} $$

(75)

$$ G_{rr} = ( - \rho \frac{L^{2}}{2} - (L + r_{s})M_{s})g $$

(76)

$$ G_{rf} = (\rho \int _{0}^{L} \int _{0}^{z_{2}} \omega _{s}\omega _{s}^{t}dsdz_{2} + M_{s}(\frac{1}{2}r_{s}\omega _{z_{2},L}\omega _{z_{2},L}^{t} + \frac{1}{2}\int _{0}^{L} \omega _{z_{2}}\omega _{z_{2}}^{t}dz_{2}))g $$

(77)

$$ G_{ff} = (\rho \int _{0}^{L} \omega ^{t}dz_{2} + M_{s}(\omega _{L}^{t} - r_{s}\omega _{z_{2},L}^{t}))g $$

(78)

$$\begin{aligned} G(X_{1}) & = \left ( \textstyle\begin{array}{c@{\quad}c@{\quad}c} 0 & 0 & 0 \\ 0 & - G_{rr} - \frac{1}{2}\delta ^{t}G_{rf}\delta & G_{ff} \\ 0 & G_{ff}^{t} & G_{rf} \end{array}\displaystyle \right )\left ( \textstyle\begin{array}{c} 0 \\ s\theta _{s} \\ c\theta _{s}\delta \end{array}\displaystyle \right ) \\ & = \left ( \textstyle\begin{array}{c} 0 \\ \left ( - G_{rr} - \frac{1}{2}\delta ^{t}G_{rf}\delta \right )s\theta _{s} + G_{ff}.c\theta _{s}\delta \\ G_{ff}^{t}.s\theta _{s} + G_{rf}.c\theta _{s}\delta \end{array}\displaystyle \right ) \end{aligned}$$

(79)

$$ C(X_{1},\dot{X}_{1}) = \left ( \textstyle\begin{array}{c} \textstyle\begin{array}{l} \frac{1}{2}( - A_{4}q.s\theta _{s} + \delta ^{t}A_{5}q.c\theta _{s} + \dot{\delta}^{t}A_{5}.s\theta _{s})\dot{\delta} \\ \quad{} + \frac{1}{2}( - \delta ^{t}A_{8}\delta q.s\theta _{s} + 2\delta ^{t}A_{8}\dot{\delta} c\theta _{s} + A_{9}\delta qc\theta _{s} + A_{9}\dot{\delta} s\theta _{s})q \end{array}\displaystyle \\ \textstyle\begin{array}{l} 2\delta ^{t}A_{3}\dot{\delta} q + \frac{1}{2}( - \delta ^{t}A_{8}\delta q.s\theta _{s} + 2\delta ^{t}A_{8}\dot{\delta} c\theta _{s} + A_{9}\delta qc\theta _{s} + A_{9}\dot{\delta} s\theta _{s})u \\ \quad{} - \frac{1}{2}( - A_{4}s\theta _{s} + \delta ^{t}A_{5}c\theta _{s})u\dot{\delta} - \frac{1}{2}( - \delta ^{t}A_{8}\delta s\theta _{s} + A_{9}\delta c\theta _{s})uq \end{array}\displaystyle \\ \textstyle\begin{array}{l} \frac{1}{2}( - A_{4}qs\theta _{s} + \delta ^{t}A_{5}qc\theta _{s} + \dot{\delta}^{t}A_{5}.s\theta _{s})^{t}u - A_{3}\delta q^{2} \\ \quad{}- \frac{1}{2}A_{5}.s\theta _{s}u\dot{\delta} - \frac{1}{2}(2A_{8}\delta c\theta _{s} + A_{9}.s\theta _{s})uq \end{array}\displaystyle \end{array}\displaystyle \right ) $$

(80)

$B$ the damping matrix:

$$ B = \left ( \textstyle\begin{array}{c@{\quad}c@{\quad}c} 0 & 0 & 0 \\ 0 & \kappa _{m} & 0 \\ 0 & 0 & B_{ff} \end{array}\displaystyle \right ) $$

(81)

$K$ the stiffness matrix:

$$ K = \left ( \textstyle\begin{array}{c@{\quad}c@{\quad}c} 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & K_{ff} \end{array}\displaystyle \right ) $$

(82)