Analytic solution for planar indeterminate impact problems using an energy constraint

Abstract

This work proposes an analytic method for resolving planar multi-point indeterminate impact problems for rigid-body systems. An event-based approach is used to detect impact events, and constraints consistent with the rigid-body assumption are used to resolve the indeterminacy associated with multi-point impact analysis. The work-energy relation is utilized to determine post-impact velocities based on an energetic coefficient of restitution to model energy dissipation, thereby yielding an energetically consistent set of post-impact velocities based on Stronge’s energetic coefficient of restitution for the treatment of rigid impacts. The effect of stick–slip transition is analyzed based on Coulomb friction. This paper also discusses the transition from impact to contact. This analysis is essential for considering the rocking block problem that is used as an example herein. The predictions of the model for the rocking block problem are compared to experimental results published in the literature. An example of a planar ball undergoing two-point impact is also presented.

Appendices

Appendix A: Energy plots

The energy plots are included here to show energy consistency for the collisions simulated for the planar rocking block (frictionless and frictional) and planar ball examples. The drops in total energy shown in Figs. 16, 17, and 18 correspond to the energy losses specified by the global ECOR and friction analyzed in the previous sections.

Fig. 16

Energy consistency throughout the simulation for (a) frictionless rocking block, and (b) frictional rocking block examples (Color figure online)

Fig. 17

Energy consistency throughout the simulation for the planar ball example (Color figure online)

Fig. 18

Energy consistency throughout the simulation for (a) Specimen 1, (b) Specimen 2, (c) Specimen 4 (Color figure online)

Appendix B: Velocity projection method

Consider for example two impact points, 1 and 2, located on a rigid body. Using classical rigid-body dynamics [77], the difference between the velocities of these two impact points is found as

$$\begin{aligned} {\mathbf{v}}_{1} - \mathbf{v}_{2} = { \boldsymbol{\omega }} \times (\mathbf{P}_{O1} - \mathbf{P}_{O2}) \end{aligned}$$

(54)

where ${\boldsymbol{\omega }}$ is the angular velocity of the body and $\mathbf{P}_{Oi}$ is the position vector of impact point $i$ with respect to the body’s mass center. If the dot product of the unit direction between impact points 1 and 2 is applied to each side of Eq. (54), such that the right-hand side is zero, then the rigid-body assumption defines

$$\begin{aligned} (\mathbf{v}_{1} - \mathbf{v}_{2}) \cdot \frac{(\mathbf{P}_{O1} - \mathbf{P}_{O2})}{|(\mathbf{P}_{O1} - \mathbf{P}_{O2})|} = 0 \end{aligned}$$

(55)

Additional rigid-body constraints can be formulated using this method with the consideration of more impact points. The benefit is clear from the simple nature of Eq. (55) and permits the definition of a kinematic relationship among a collection of impact points on a rigid body.

2.1 B.1 Rocking block

Evaluating the terms involved in the constraint for the planar rocking block yields

$$\begin{aligned} \bigl( (v_{t1} - v_{t2}) \mathbf{N}_{1} + (v_{n1} - v_{n2}) \mathbf{N} _{2} \bigr) \cdot ( -\mathbf{N_{1}} ) = v_{t1} - v _{t2} = 0 \end{aligned}$$

(56)

The velocity constraint obtained in Eq. (56) is used to constrain one of the tangential velocities. Consider an example where $v_{t1}$ is constrained. This is accomplished by solving for this velocity term and substituting the expression into Eq. (58) which gives,

$$\begin{aligned} {\boldsymbol{\vartheta }} = \left[ \textstyle\begin{array}{c} v_{t1} \\ v_{n1} \\ v_{t2} \\ v_{n2} \\ \end{array}\displaystyle \right] = \left[ \textstyle\begin{array}{c} v_{t2} \\ v_{n1} \\ v_{t2} \\ v_{n2} \\ \end{array}\displaystyle \right] = \left [ \textstyle\begin{array}{c@{\quad }c@{\quad }c} 0 & 1 & 0 \\ 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{array}\displaystyle \right ] \left [ \textstyle\begin{array}{c} v_{n1} \\ v_{t2} \\ v_{n2} \end{array}\displaystyle \right ] = \textstyle\begin{array}{c} P\ {\boldsymbol{\vartheta }}^{*} \\ \end{array}\displaystyle \end{aligned}$$

(57)

where $P$ is a matrix of full rank containing the velocity constraint and ${\boldsymbol{\vartheta }}^{*}$ contains the constrained velocity space. The dual property of the impact Jacobian defines a relationship between velocities and forces, which is derived based on the principle of virtual work and conservation of energy theory [78],

$$\begin{aligned} {\boldsymbol{\vartheta }} = \left[ \textstyle\begin{array}{c} v_{t1} \\ v_{n1} \\ v_{t2} \\ v_{n2} \end{array}\displaystyle \right] = J \dot{\mathbf{q}} ,\quad \quad {\boldsymbol{\varGamma }} = J^{T} \mathbf{F} = J^{T} \left[ \textstyle\begin{array}{c} f_{t1} \\ f_{n1} \\ f_{t2} \\ f_{n2} \end{array}\displaystyle \right] \end{aligned}$$

(58)

such that

$$\begin{aligned} {\boldsymbol{\varGamma }} = J^{T} \mathbf{F} = J^{T} \bigl(P^{+} \bigr)^{T} \mathbf{F}^{*} \end{aligned}$$

(59)

Equation (59) yields

$$\begin{aligned} {\mathbf{F}} = \bigl( P^{+} \bigr) ^{T} \mathbf{F}^{*} \quad \mbox{or} \quad P^{T} \mathbf{F} = \mathbf{F}^{*} \end{aligned}$$

(60)

where $P^{+}$ is the left-inverse of $P$. It is incorrect to assume that the constrained force space $\mathbf{F}^{*}$ will involve the same terms as in the constrained velocity space ${\boldsymbol{\vartheta }}^{*}$. Therefore, consider the second expression in Eq. (60) where $\mathbf{F}^{*}$ is solved:

$$\begin{aligned} {\mathbf{F}}^{*} = P^{T} \mathbf{F} = \left[ \textstyle\begin{array}{c@{\quad }c@{\quad }c@{\quad }c} 0 & 1 & 0 & 0 \\ 1 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{array}\displaystyle \right] \left [ \textstyle\begin{array}{c} f_{t1} \\ f_{n1} \\ f_{t2} \\ f_{n2} \end{array}\displaystyle \right ] = \left [ \textstyle\begin{array}{c} f_{n1} \\ f_{t1} + f_{t2} \\ f_{n2} \end{array}\displaystyle \right ] \end{aligned}$$

(61)

such that

$$\begin{aligned} \left[ \textstyle\begin{array}{c} f_{t1} \\ f_{n1} \\ f_{t2} \\ f_{n2} \end{array}\displaystyle \right] = \mathbf{F} = \bigl(P^{+} \bigr)^{T} \mathbf{F}^{*} = \left [ \textstyle\begin{array}{c@{\quad }c@{\quad }c} 0 & 0.5 & 0 \\ 1 & 0 & 0 \\ 0 & 0.5 & 0 \\ 0 & 0 & 1 \end{array}\displaystyle \right ] \left [ \textstyle\begin{array}{c} f_{n1} \\ f_{t1} + f_{t2} \\ f_{n2} \end{array}\displaystyle \right ] = \left [ \textstyle\begin{array}{c} 0.5 ( f_{t1} + f_{t2} ) \\ f_{n1} \\ 0.5 ( f_{t1} + f_{t2} ) \\ f_{n2} \end{array}\displaystyle \right ] \end{aligned}$$

(62)

The first and third relations yield the same force constraint,

$$\begin{aligned} f_{t1} - f_{t2} = 0 \end{aligned}$$

(63)

Applying a definite integration of Eq. (63), the constraint is expressed in terms of impulses as

$$\begin{aligned} p_{t1} - p_{t2} = 0 \end{aligned}$$

(64)

Note that for a frictionless case ($\mu_{i} = 0$) the tangential forces vanish, which eliminates the indeterminacy in the system equations of motion.

2.2 B.2 Planar ball

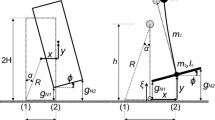
Evaluating the terms involved in the constraint for the planar ball shown in Fig. 1(b) yields

$$\begin{aligned} \bigl( (v_{t1} - v_{n2}) \mathbf{N}_{1} + (v_{n1} - v _{t2}) \mathbf{N}_{2} \bigr) \cdot \biggl( -\frac{1}{\sqrt{2}} \mathbf{N_{1}} - \frac{1}{\sqrt{2}} \mathbf{N_{2}} \biggr) = -v _{t1} - v_{n1} + v_{t2} + v_{n2} = 0 \end{aligned}$$

(65)

The velocity constraint obtained in Eq. (65) is used to constrain one of the tangential velocities. Consider an example where $v_{t1}$ is constrained. This is accomplished by solving for this velocity term in Eq. (65) which gives

$$\begin{aligned} {\boldsymbol{\vartheta }} = \left[ \textstyle\begin{array}{c} v_{t1} \\ v_{n1} \\ v_{t2} \\ v_{n2} \\ \end{array}\displaystyle \right] = \left[ \textstyle\begin{array}{c} -v_{n1} + v_{t2} + v_{n2} \\ v_{n1} \\ v_{t2} \\ v_{n2} \\ \end{array}\displaystyle \right] = \left [ \textstyle\begin{array}{c@{\quad }c@{\quad }c} -1 & 1 & 1 \\ 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{array}\displaystyle \right ] \left [ \textstyle\begin{array}{c} v_{n1} \\ v_{t2} \\ v_{n2} \end{array}\displaystyle \right ] = P {\boldsymbol{\vartheta }}^{*} \end{aligned}$$

(66)

where $P$ is a matrix of full rank containing the velocity constraint and ${\boldsymbol{\vartheta }}^{*}$ contains the constrained velocity space. Applying the dual property of the impact Jacobian and solving for the constrained force space yields

$$\begin{aligned} {\mathbf{F}}^{*} = P^{T} \mathbf{F} = \left[ \textstyle\begin{array}{c@{\quad }c@{\quad }c@{\quad }c} -1 & 1 & 0 & 0 \\ 1 & 0 & 1 & 0 \\ 1 & 0 & 0 & 1 \end{array}\displaystyle \right] \left [ \textstyle\begin{array}{c} f_{t1} \\ f_{n1} \\ f_{t2} \\ f_{n2} \end{array}\displaystyle \right ] = \left [ \textstyle\begin{array}{c} -f_{t1} + f_{n1} \\ f_{t1} + f_{t2} \\ f_{t1} + f_{n2} \end{array}\displaystyle \right ] \end{aligned}$$

(67)

Using this result in the first relation in Eq. (60) gives

$$\begin{aligned} \left[ \textstyle\begin{array}{c} f_{t1} \\ f_{n1} \\ f_{t2} \\ f_{n2} \end{array}\displaystyle \right] = &\mathbf{F} = \bigl(P^{+} \bigr)^{T} \mathbf{F}^{*} = \left [ \textstyle\begin{array}{c@{\quad }c@{\quad }c} -0.25 & 0.25 & 0.25 \\ 0.75 & 0.25 & 0.25 \\ 0.25 & 0.75 & -0.25 \\ 0.25 & -0.25 & 0.75 \end{array}\displaystyle \right ] \left [ \textstyle\begin{array}{c} -f_{t1} + f_{n1} \\ f_{t1} + f_{t2} \\ f_{t1} + f_{n2} \end{array}\displaystyle \right ] \\ =& \left [ \textstyle\begin{array}{c} 0.75 f_{t1} - 0.25 f_{n1} + 0.25 f_{t2} + 0.25 f_{n2} \\ -0.25 f_{t1} + 0.75 f_{n1} + 0.25 f_{t2} + 0.25 f_{n2} \\ 0.25 f_{t1} + 0.25 f_{n1} + 0.75 f_{t2} - 0.25 f_{n2} \\ 0.25 f_{t1} + 0.25 f_{n1} - 0.25 f_{t2} + 0.75 f_{n2} \end{array}\displaystyle \right ] \end{aligned}$$

(68)

such that every relation in Eq. (68) yields the same force constraint:

$$\begin{aligned} f_{t1} + f_{n1} - f_{t2} - f_{n2} = 0 \end{aligned}$$

(69)

Applying a definite integration of Eq. (69), the constraint is expressed in terms of impulses as

$$\begin{aligned} p_{t1} + p_{n1} - p_{t2} - p_{n2} = 0 \end{aligned}$$

(70)

Note again that for a frictionless case ($\mu_{i} = 0$) the tangential forces vanish, which eliminates the indeterminacy in the system equations of motion.