Skip to main content
SpringerLink
Log in

Optimization-based dynamic prediction of kinematic and kinetic patterns for a human vertical jump from a squatting position

  • Published:
Multibody System Dynamics Aims and scope Submit manuscript

Abstract

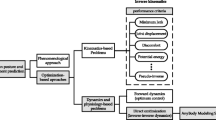
This paper presents the prediction of kinematic and kinetic patterns for human squat jumping using an optimization-based dynamic human movement prediction technique. This method enables prediction of realistic kinematics and kinetics in human squat vertical jumping including muscle and joint forces. The case of vertical jumping is selected because the criterion is clear: to maximize the jump height. First, an anatomically detailed three-dimensional human squat jump model was developed. The movement was then parameterized by means of time functions controlling selected degrees-of-freedom (DOF) of the model. Subsequently, the optimizer found the parameters of these functions to maximize the jump height subject to anatomical and physiological constraints. The results were compared with experimental data from a group of six healthy males. Qualitative and quantitative comparisons between predicted results and experimental observations indicate that the approach is capable of predicting the jump height enhancement in squat vertical jumping with arm swing and reproducing the coordinated motion in terms of kinetics and kinematics.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17
Fig. 18
Fig. 19
Fig. 20
Fig. 21
Fig. 22
Fig. 23

Similar content being viewed by others

References

  1. Rasmussen, J., Christensen, S.T., Gföhler, M., Damsgaard, M., Angeli, T.: Design optimization of a pedaling mechanism for paraplegics. Struct. Multidiscip. Optim. 26, 132–138 (2004)

    Article  Google Scholar 

  2. Rasmussen, J., Holmberg, L.J., Sørensen, K., Kwan, M., Andersen, M.S., de Zee, M.: Performance optimization by musculoskeletal simulation. Mov. Sport Sci. 1, 73–83 (2012)

    Article  Google Scholar 

  3. Lemieux, P.O., Tetreault, P., Hagemeister, N., Nuno, N.: Influence of prosthetic humeral head size and medial offset on the mechanics of the shoulder with cuff tear arthropathy: A numerical study. J. Biomech. 46, 806–812 (2013)

    Article  Google Scholar 

  4. Mellon, S.J., Grammatopoulos, G., Andersen, M.S., Pegg, E.C., Pandit, H.G., Murray, D.W., Gill, H.S.: Individual motion patterns during gait and sit-to-stand contribute to edge-loading risk in metal-on-metal hip resurfacing. Proc. Inst. Mech. Eng., H J. Eng. Med. 227, 799–810 (2013)

    Article  Google Scholar 

  5. Weber, T., Dendorfer, S., Dullien, S., Grifka, J., Verkerke, G.J., Renkawitz, T.: Measuring functional outcome after total hip replacement with subject-specific hip joint loading. Proc. Inst. Mech. Eng., H J. Eng. Med. 226, 939–946 (2012)

    Article  Google Scholar 

  6. Grujicic, M., Pandurangan, B., Xie, X., Gramopadhye, A.K., Wagner, D., Ozen, M.: Musculoskeletal computational analysis of the influence of car-seat design/adjustments on long-distance driving fatigue. Int. J. Ind. Ergon. 40, 345–355 (2010)

    Article  Google Scholar 

  7. Rasmussen, J., Tørholm, S., de Zee, M.: Computational analysis of the influence of seat pan inclination and friction on muscle activity and spinal joint forces. Int. J. Ind. Ergon. 39, 52–57 (2009)

    Article  Google Scholar 

  8. Rasmussen, J., Davoudabadi Farahani, S.: Simulating the effect of support points in manual mounting operations. In: International Summit on Human Simulation, Florida, United States (2011)

    Google Scholar 

  9. Damiano, D.L., Arnold, A.S., Steele, K.M., Delp, S.L.: Can strength training predictably improve gait kinematics? A pilot study on the effects of hip and knee extensor strengthening on lower-extremity alignment in cerebral palsy. Phys. Ther. 90, 269–279 (2010)

    Article  Google Scholar 

  10. Lampire, N., Roche, N., Carne, P., Cheze, L., Pradon, D.: Effect of botulinum toxin injection on length and lengthening velocity of rectus femoris during gait in hemiparetic patients. Clin. Biomech. 28, 164–170 (2013)

    Article  Google Scholar 

  11. Erdemir, A., McLean, S., Herzog, W., Van den Bogert, A.J.: Model-based estimation of muscle forces exerted during movements. Clin. Biomech. 22, 131–154 (2007)

    Article  Google Scholar 

  12. Pandy, M.G., Zajac, F.E., Sim, E., Levine, W.S.: An optimal control model for maximum-height human jumping. J. Biomech. 23, 1185–1198 (1990)

    Article  Google Scholar 

  13. Zajac, F.E.: Muscle coordination of movement: A perspective. J. Biomech. 26, 109–124 (1993)

    Article  Google Scholar 

  14. Anderson, F.C., Pandy, M.G.: A dynamic optimization solution for vertical jumping in three dimensions. Comput. Methods Biomech. Biomed. Eng. 2, 201–231 (1999)

    Article  Google Scholar 

  15. Anderson, F.C., Pandy, M.G.: Dynamic optimization of human walking. J. Biomech. Eng. 123, 381–390 (2001)

    Article  Google Scholar 

  16. Glitsch, U., Baumann, W.: The three-dimensional determination of internal loads in the lower extremity. J. Biomech. 30, 1123–1131 (1997)

    Article  Google Scholar 

  17. Crowninshield, R.D., Brand, R.A.: A physiologically based criterion of muscle force prediction in locomotion. J. Biomech. 14, 793–801 (1981)

    Article  Google Scholar 

  18. Rasmussen, J., Damsgaard, M., Voigt, M.: Muscle recruitment by the min/max criterion: A comparative numerical study. J. Biomech. 34, 409–415 (2001)

    Article  Google Scholar 

  19. Rasmussen, J., Damsgaard, M., Christensen, S.T.: Inverse–inverse dynamics simulation of musculo-skeletal systems. In: Proceedings of the 12th Conference of the European Society of Biomechanics, Royal Academy of Medicine in Ireland (2000). ISBN 0-9538809-0-7

    Google Scholar 

  20. Abdel-Malek, K., Arora, J.S.: Human Motion Simulation: Predictive Dynamics. Elsevier, Amsterdam (2013)

    Google Scholar 

  21. Marler, R.T., Arora, J.S., Yang, J., Kim, H.J., Abdel-Malek, K.: Use of multi-objective optimization for digital human posture prediction. Eng. Optim. 41, 925–943 (2009)

    Article  Google Scholar 

  22. Mi, Z., Yang, J., Abdel-Malek, K.: Optimization-based posture prediction for human upper body. Robotica 27, 607–620 (2009)

    Article  Google Scholar 

  23. Abdel-Malek, K., Mi, Z., Yang, J., Nebel, K.: Optimization-based trajectory planning of the human upper body. Robotica 24, 683–696 (2006)

    Article  Google Scholar 

  24. Ackermann, M., van den Bogert, A.J.: Optimality principles for model-based prediction of human gait. J. Biomech. 43, 1055–1060 (2010)

    Article  Google Scholar 

  25. Kim, J.H., Abdel-Malek, K., Yang, J., Marler, R.T.: Prediction and analysis of human motion dynamics performing various tasks. Int. J. Hum. Factors Model. Simul. 1, 69–94 (2006)

    Article  Google Scholar 

  26. Xiang, Y., Arora, J.S., Rahmatalla, S., Marler, T., Bhatt, R., Abdel-Malek, K.: Human lifting simulation using a multi-objective optimization approach. Multibody Syst. Dyn. 23, 1–21 (2010)

    Article  MATH  MathSciNet  Google Scholar 

  27. Xiang, Y., Arora, J.S., Rahmatalla, S., Abdel-Malek, K.: Optimization-based dynamic human walking prediction: One step formulation. Int. J. Numer. Methods Eng. 79, 667–695 (2009)

    Article  MATH  Google Scholar 

  28. Xiang, Y., Arora, J.S., Abdel-Malek, K.: Physics-based modeling and simulation of human walking: A review of optimization-based and other approaches. Struct. Multidiscip. Optim. 42, 1–23 (2010)

    Article  MATH  MathSciNet  Google Scholar 

  29. Xiang, Y., Chung, H.J., Kim, J.H., Bhatt, R., Rahmatalla, S., Yang, J., Marler, T., Arora, J.S., Abdel-Malek, K.: Predictive dynamics: An optimization-based novel approach for human motion simulation. Struct. Multidiscip. Optim. 41, 465–479 (2010)

    Article  MATH  MathSciNet  Google Scholar 

  30. Xiang, Y., Arora, J.S., Abdel-Malek, K.: Optimization-based prediction of asymmetric human gait. J. Biomech. 44, 683–693 (2011)

    Article  Google Scholar 

  31. Bobbert, M.F., van Soest, A.J.: Why do people jump the way they do? Exerc. Sport Sci. Rev. 29, 95–102 (2001)

    Article  Google Scholar 

  32. Bobbert, M.F., Casius, L.R., Sijpkens, I.W., Jaspers, R.T.: Humans adjust control to initial squat depth in vertical squat jumping. Int. J. Appl. Phys. 105, 1428–1440 (2008)

    Google Scholar 

  33. Blache, Y., Monteil, K.: Effect of arm swing on effective energy during vertical jumping: Experimental and simulation study. Scand. J. Med. Sci. Sports 23, 121–129 (2013)

    Article  Google Scholar 

  34. Damsgaard, M., Rasmussen, J., Christensen, S.T., Surma, E., de Zee, M.: Analysis of musculoskeletal systems in the AnyBody Modeling System. Simul. Model. Pract. Theory 14, 1100–1111 (2006)

    Article  Google Scholar 

  35. Andersen, M.S., Damsgaard, M., Rasmussen, J.: Kinematic analysis of over-determinate biomechanical systems. Comput. Methods Biomech. Biomed. Eng. 12, 371–384 (2009)

    Article  Google Scholar 

  36. Andersen, M.S., Damsgaard, M., MacWilliams, B., Rasmussen, J.: A computationally efficient optimisation-based method for parameter identification of kinematically determinate and over-determinate biomechanical systems. Comput. Methods Biomech. Biomed. Eng. 13, 171–183 (2010)

    Article  Google Scholar 

  37. Rasmussen, J., de Zee, M., Damsgaard, M., Christensen, S.T., Marek, C., Siebertz, K.: A general method for scaling musculo-skeletal models. International Symposium on Computer Simulation in Biomechanics, United States (2005)

    Google Scholar 

  38. Delp, S.L.: Surgery simulation: A computer graphics system to analyze and design musculoskeletal reconstructions of the lower limb. Ph.D. thesis, Department of Mechanical Engineering, Stanford University, Stanford, CA (1990)

  39. Delp, S.L., Loan, J.P., Hoy, M.G., Zajac, F.E., Topp, E.L., Rosen, J.M.: An interactive graphics-based model of the lower extremity to study orthopaedic surgical procedures. IEEE Trans. Biomed. Eng. 37, 757–767 (1990)

    Article  Google Scholar 

  40. Box, M.: A new method of constrained optimization and a comparison with other methods. Comput. J. 8, 42–52 (1965)

    Article  MATH  MathSciNet  Google Scholar 

  41. Sprague, M.A., Geers, T.L.: Spectral elements and field separation for an acoustic fluid subject to cavitation. J. Comput. Phys. 184, 149–162 (2003)

    Article  MATH  Google Scholar 

  42. Geers, T.L.: An objective error measure for the comparison of calculated and measured transient response histories. Shock Vib. Bull. 54, 99–107 (1984)

    Google Scholar 

  43. Schwer, L.E.: Validation metrics for response histories: Perspectives and case studies. Eng. Comput. 23, 295–309 (2007)

    Article  Google Scholar 

  44. Lund, M.E., de Zee, M., Rasmussen, J.: Comparing calculated and measured curves in validation of musculoskeletal models. In: The XIII International Symposium on Computer Simulation in Biomechanics, Leuven, Belgium (2011)

    Google Scholar 

  45. Bobbert, M.F., van Ingen Schenau, G.J.: Coordination in vertical jumping. J. Biomech. 21, 249–262 (1988)

    Article  Google Scholar 

  46. Bobbert, M.F., van Zandwijk, J.P.: Dynamics of force and muscle stimulation in human vertical jumping. Med. Sci. Sports Exerc. 31, 303–310 (1999)

    Article  Google Scholar 

  47. Hara, M., Shibayama, A., Takeshita, D., Fukashiro, S.: The effect of arm swing on lower extremities in vertical jumping. J. Biomech. 39, 2503–2511 (2006)

    Article  Google Scholar 

Download references

Acknowledgements

This work was supported by the Danish Advanced Technology Foundation.

Author information

Authors and Affiliations

  1. AnyBody Research Group, Department of Mechanical and Manufacturing Engineering, Aalborg University, 9220, Aalborg East, Denmark

    Saeed Davoudabadi Farahani, Michael Skipper Andersen, Mark de Zee & John Rasmussen

  2. Center for Sensory-Motor Interaction, Department of Health Science and Technology, Aalborg University, 9220, Aalborg East, Denmark

    Mark de Zee

Authors
  1. Saeed Davoudabadi Farahani
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Michael Skipper Andersen
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Mark de Zee
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. John Rasmussen
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Saeed Davoudabadi Farahani.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Davoudabadi Farahani, S., Andersen, M.S., de Zee, M. et al. Optimization-based dynamic prediction of kinematic and kinetic patterns for a human vertical jump from a squatting position. Multibody Syst Dyn 36, 37–65 (2016). https://doi.org/10.1007/s11044-015-9468-5

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11044-015-9468-5

Keywords

Search

Navigation