Abstract
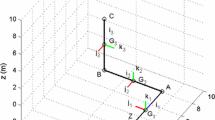
The generalized coordinates partitioning is a well-known procedure that can be applied in the framework of a numerical integration of the DAE systems. However, although the procedure proves to be a very useful tool, it is known that an optimization algorithm for the coordinates partitioning is needed to obtain the best performance. In the paper, the optimized partitioning of the generalized coordinates is revisited in the context of a numerical forward dynamics of the holonomic and non-holonomic multibody systems. After a short presentation of the geometric background of the optimized coordinates partitioning, a structure of the optimally partitioned vectors is discussed on the basis of a gradient analysis of the separate constraint sub-manifolds at the configuration and the velocity levels when holonomic and non-holonomic constraints are present in the system. It is shown that, for holonomic systems, the vectors of optimally partitioned coordinates have the same structure for the generalized positions and velocities. On the contrary, in the case of non-holonomic systems, the optimally partitioned coordinates generally differ at the configuration and the velocity levels. The conclusions of the paper are illustrated within the framework of the presented numerical example.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
Wehage, R.A., Haug, E.J.: Generalized coordinate partitioning for dimension reduction in analysis of constrained dynamic systems. J. Mech. Des. 104, 247–255 (1982)
Nikravesh, P.E.: Computer-Aided Analysis of Mechanical Systems. Prentice Hall, New York (1988)
Haug, E.J.: Computer Aided Kinematics and Dynamics of Mechanical Systems: Basic Methods. Prentice Hall, New York (1989)
Schiehlen, W.: Multibody system dynamics: roots and perspectives. Multibody Syst. Dyn. 1, 149–188 (1997)
Terze, Z., Lefeber, D., Muftić, O.: Null space integration method for constrained multibody system simulation with no constraint violation. Multibody Syst. Dyn. 6, 229–243 (2001)
Terze, Z., Naudet, J.: Geometric properties of projective constraint violation stabilization method for generally constrained multibody systems on manifolds. Multibody Syst. Dyn. 20, 85–106 (2008)
Blajer, W., Schiehlen, W., Schirm, W.: A projective criterion to the coordinate partitioning method for multibody dynamics. Arch. Appl. Mech. 64, 86–98 (1994)
Blajer, W.: Elimination of constraint violation and accuracy aspects in numerical simulation of multibody systems. Multibody Syst. Dyn. 7(3), 265–284 (2002)
Marsden, J.E., Ratiu, T.S.: Introduction to Mechanics and Symmetry. Springer, New York (1999)
Arnold, V.I.: Mathematical Methods of Classical Mechanics. Springer, New York (1978)
Bullo, F., Lewis, A.D.: Geometric Control of Mechanical Systems. Springer, New York (2005)
Shutz, B.F.: Geometrical Methods of Mathematical Physics. Cambridge Univ. Press, Cambridge (1980)
Jungnickel, U.: Differential-algebraic equations in Riemannian spaces and applications to multibody system dynamics. ZAMM 74, 409–415 (1994)
Blajer, W.: A geometric unification of constrained system dynamics. Multibody Syst. Dyn. 1, 3–21 (1997)
de Jalon, J.G., Bayo, E.: Kinematic and Dynamic Simulation of Multibody Systems: The Real-Time Challenge. Springer, New York (1994)
Terze, Z., Müller, A.: Lie group modeling and forward dynamics simulation of multibody systems, part 2: dynamics and time integration. Trans. FAMENA 33(3), 1–14 (2009)
Nikravesh, P.E.: Initial condition correction in multibody dynamics. Multibody Syst. Dyn. 18, 107–115 (2007)
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Terze, Z., Naudet, J. Structure of optimized generalized coordinates partitioned vectors for holonomic and non-holonomic systems. Multibody Syst Dyn 24, 203–218 (2010). https://doi.org/10.1007/s11044-010-9195-x
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11044-010-9195-x