Skip to main content
SpringerLink
Log in

Analysis of multibody systems experiencing large elastic deformations

  • Published:
Multibody System Dynamics Aims and scope Submit manuscript

Abstract

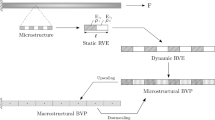
This study presents an approach based on the floating frame of reference method to model complex three-dimensional bodies in a multibody system using solid and plate elements. Unlike most of the formulations based on the floating frame of reference method, which assume small or moderate deformations, the present formulation allows large elastic deformations within each frame by using the corotational form of the updated Lagrangian description of motion. The implicit integration scheme is based on the Generalized-α method, and kinematic joints are invoked in the formulation through the coordinate partitioning method. A triangular element with three nodes and a solid wedge element with six nodes have been developed to facilitate the modeling of three-dimensional bodies with arbitrary geometry. Various numerical examples have been considered to demonstrate the robustness of the present approach.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Schiehlen, W.O.: Multibody system dynamics—roots and perspectives. Multibody Syst. Dyn. 1, 149–188 (1997)

    Article  MATH  MathSciNet  Google Scholar 

  2. Wasfy, T.M., Noor, A.K.: Computational strategies for flexible multibody systems. Appl. Mech. Rev. 56, 553–613 (2003)

    Article  Google Scholar 

  3. Shabana, A.A.: Flexible multibody dynamics: review of past and recent developments. Multibody Syst. Dyn. 1, 189–222 (1997)

    Article  MATH  MathSciNet  Google Scholar 

  4. Kane, T.R., Ryan, R.R., Banerjee, A.K.: Dynamics of a cantilever beam attached to a moving base. J. Guid. Control Dyn. 10, 139–151 (1987)

    Article  Google Scholar 

  5. Banerjee, A.K.: Contributions of multibody dynamics to space flight: a brief review. J. Guid. Control Dyn. 26, 385–394 (2003)

    Article  Google Scholar 

  6. Banerjee, A.K., Dickens, J.M.: Dynamics of an arbitrary flexible body in large rotation and translation. J. Guid. Control Dyn. 13, 221–227 (1990)

    Article  Google Scholar 

  7. Bakr, E.M., Shabana, A.A.: Geometrically nonlinear analysis of multibody systems. Comput. Struct. 23, 739–751 (1986)

    Article  MATH  Google Scholar 

  8. Ider, S.K., Amirouche, F.M.L.: Influence of geometric nonlinearities on the dynamics of flexible tree-like structures. J. Guid. Control Dyn. 12, 830–837 (1989)

    Article  MATH  MathSciNet  Google Scholar 

  9. Mayo, J., Dominguez, J.: Geometrically nonlinear formulation flexible multibody systems in terms of beam elements: geometric stiffness. Comput. Struct. 59, 1039–1050 (1996)

    Article  MATH  Google Scholar 

  10. Ryu, J., Kim, S.S., Kim, S.S.: A criterion on inclusion of stress stiffening effects in flexible multibody dynamic system simulation. Comput. Struct. 62(6), 1035–1048 (1997)

    Article  MATH  Google Scholar 

  11. Wallrapp, O., Schwertassek, R.: Representation of geometric stiffening in multibody system simulation. Int. J. Numer. Methods Eng. 32, 1833–1850 (1991)

    Article  MATH  Google Scholar 

  12. Mayo, J.M., García-Vallejo, D., Domínguez, J.: Study of the geometric stiffening effect: comparison of different formulations. Multibody Syst. Dyn. 11, 321–341 (2004)

    Article  MATH  Google Scholar 

  13. Sharf, I.: Geometric stiffening in multibody dynamics formulations. J. Guid. Control Dyn. 18, 882–890 (1995)

    Article  MATH  Google Scholar 

  14. Liu, A.Q., Liew, K.M.: Non-linear substructure approach for dynamic analysis of rigid flexible multibody systems. Comput. Methods Appl. Mech. Eng. 114, 379–390 (1994)

    Article  Google Scholar 

  15. Wu, S.C., Haug, E.J.: Geometric non-linear substructuring for dynamics of flexible mechanical systems. Int. J. Numer. Methods Eng. 26, 2211–2226 (1988)

    Article  MATH  Google Scholar 

  16. Shabana, A.A.: Dynamics of Multibody Systems, 3rd edn. Cambridge University Press, Cambridge (2005)

    MATH  Google Scholar 

  17. Tsang, T.Y., Arabyan, A.: A novel approach to the dynamic analysis of highly deformable bodies. Comput. Struct. 58, 155–172 (1996)

    Article  MATH  MathSciNet  Google Scholar 

  18. Iura, M., Atluri, S.N.: Dynamic analysis of planar flexible beams with finite rotations by using inertial and rotating frames. Comput. Struct. 55, 453–462 (1995)

    Article  MATH  Google Scholar 

  19. Ambrosio, J.: Geometric and material nonlinear deformations in flexible multibody systems. In: Ambrosio, J.A.C., Kleiber, M. (eds.) Computational Aspects of Nonlinear Structural Systems with Large Rigid Body Motion, pp. 3–27. IOS Press, Amsterdam (2001)

    Google Scholar 

  20. Vetyukov, Y.: Consistent approximation for the strain energy of a 3D elastic body adequate for the stress stiffening effect. Int. J. Struct. Stab. Dyn. 4, 279–292 (2004)

    Article  Google Scholar 

  21. Gerstmayr, J.: Strain tensors in the absolute nodal coordinate and the floating frame of reference formulation. Int. J. Nonlinear Dyn. 34, 133–145 (2003)

    Article  MATH  MathSciNet  Google Scholar 

  22. Vetyukov, Yu., Gerstmayr, J., Irschik, H.: The comparative analysis of the fully nonlinear and consistently linearized equations of motion of the 2D elastic pendulum. J. Comput. Struct. 82, 863–870 (2004)

    Article  Google Scholar 

  23. Rankin, C.C., Brogan, F.A.: An element corotational procedure for treatment of large rotations. ASME J. Pressure Vessel Tech. 108, 165–174 (1986)

    Article  Google Scholar 

  24. Belytschko, T., Hsieh, B.J.: Nonlinear transient finite element analysis with convected coordinates. Int. J. Numer. Methods Eng. 7, 255–271 (1973)

    Article  MATH  Google Scholar 

  25. Wehage, R., Haug, E.: Generalized coordinate partitioning for dimension reduction in analysis of constrained dynamic systems. ASME J. Mech. Des. 134, 247–255 (1982)

    Google Scholar 

  26. Chung, J., Hulbert, G.M.: Time integration algorithm for structural dynamics with improved numerical dissipation: the generalized- alpha method. J. Appl. Mech. 60, 371–375 (1993)

    Article  MATH  MathSciNet  Google Scholar 

  27. Banerjee, A.K., Kane, T.R.: Dynamics of a plate in large overall motion. ASME J. Appl. Mech. 56, 887–892 (1989)

    MATH  Google Scholar 

  28. Boutaghou, Z.E., Erdman, A.G., Stolarsi, H.K.: Dynamics of flexible beams and plates in large overall motions. ASME J. Appl. Mech. 59, 991–999 (1992)

    MATH  Google Scholar 

  29. Chang, B., Shabana, A.A.: Nonlinear finite element formulation for the large displacement analysis of plates. ASME J. Appl. Mech. 57, 707–718 (1990)

    MATH  Google Scholar 

  30. Chang, B., Shabana, A.A.: Total Lagrangian formulation for the large displacement analysis of rectangular plates. Int. J. Numer. Methods Eng. 29, 73–103 (1990)

    Article  MATH  Google Scholar 

  31. Kremer, J.M., Shabana, A.A., Widern, G.E.: Large reference displacement analysis of composite plates, parts I and II. Int. J. Numer. Methods Eng. 36, 1–42 (1993)

    Article  MATH  Google Scholar 

  32. Madenci, E., Barut, A.: Dynamic response of thin composite shells experiencing non-linear elastic deformation coupled with large and rapid overall motion. Int. J. Numer. Methods Eng. 39, 2695–2723 (1996)

    Article  MATH  Google Scholar 

  33. Barut, A., Madenci, E., Tessler, A.: Nonlinear elastic deformations of moderately thick laminated shells subjected to large and rapid rigid-body motion. Finite Elem. Anal. Des. 22, 41–57 (1996)

    Article  MATH  MathSciNet  Google Scholar 

  34. Hilber, H.H., Hughes, T.J.R., Taylor, R.L.: Improved numerical dissipation for time integration algorithms in structural dynamics. Earthq. Eng. Struct. Dyn. 5, 293–292 (1977)

    Article  Google Scholar 

  35. Wood, W.L., Bossak, M., Zienkiewicz, O.C.: An alpha modification of Newmark’s method. Inter. J. Numer. Methods Eng. 15, 1562–1566 (1981)

    Article  MathSciNet  Google Scholar 

  36. Simo, J.C., Vu-Quoc, L.: On the dynamics on flexible beams under large overall motions-the plane case: part I and II. ASME J. Appl. Mech. 53, 849–863 (1986)

    Article  MATH  Google Scholar 

  37. Bauchau, O.A., Choi, J.Y., Bottasso, C.L.: On the modeling of shells in multibody dynamics. Multibody Syst. Dyn. 8, 459–489 (2002)

    Article  MATH  Google Scholar 

  38. Wilson, E.L., Taylor, R.L., Doherty, W.P., Ghaboussi, J.: Incompatible displacement models. In: Fenves, S.J. (ed.) Numerical and Computational Methods in Structural Mechanics, pp. 43–57. Academic Press, New York (1973)

    Google Scholar 

  39. Taylor, R.L., Beresford, P.J., Wilson, E.L.: A non-conforming element for stress analysis. Inter. J. N. Methods Eng. 10, 1211–1219 (1976)

    Article  MATH  Google Scholar 

  40. Tessler, A.: A C 0-anisoparametric three-noded shell element. Comput. Methods Appl. Mech. Eng. 78, 89–103 (1990)

    Article  MATH  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Aerospace and Mechanical Engineering, The University of Arizona, Tucson, Arizona, USA

    Manabendra Das, Atila Barut & Erdogan Madenci

Authors
  1. Manabendra Das
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Atila Barut
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Erdogan Madenci
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Erdogan Madenci.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Das, M., Barut, A. & Madenci, E. Analysis of multibody systems experiencing large elastic deformations. Multibody Syst Dyn 23, 1–31 (2010). https://doi.org/10.1007/s11044-009-9168-0

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11044-009-9168-0

Keywords

Search

Navigation