Abstract
We introduce a new function, the apparent elastic modulus strain-rate spectrum, \(E_{\mathrm{app}} ( \dot{\varepsilon} )\), for the derivation of lumped parameter constants for Generalized Maxwell (GM) linear viscoelastic models from stress-strain data obtained at various compressive strain rates (\(\dot{\varepsilon}\)). The \(E_{\mathrm{app}} ( \dot{\varepsilon} )\) function was derived using the tangent modulus function obtained from the GM model stress-strain response to a constant \(\dot{\varepsilon}\) input. Material viscoelastic parameters can be rapidly derived by fitting experimental \(E_{\mathrm{app}}\) data obtained at different strain rates to the \(E_{\mathrm{app}} ( \dot{\varepsilon} )\) function. This single-curve fitting returns similar viscoelastic constants as the original epsilon dot method based on a multi-curve global fitting procedure with shared parameters. Its low computational cost permits quick and robust identification of viscoelastic constants even when a large number of strain rates or replicates per strain rate are considered. This method is particularly suited for the analysis of bulk compression and nano-indentation data of soft (bio)materials.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Avoid common mistakes on your manuscript.
1 Introduction
To date, different testing and analysis methods are used to derive quantitative mechanical properties for describing intrinsic material behavior and predicting material responses under specific loading conditions (Mattei and Ahluwalia 2016). Although mechanical characterization is often limited to the derivation of elastic properties, many materials, such as soft tissues and hydrogels, are known to exhibit viscoelastic behavior with time-dependent responses (Fung 1993; Mattei et al. 2014, 2015b, 2017a; Oyen 2013; Tirella et al. 2014; Zhao et al. 2010). Creep and stress-relaxation tests are among the most common methods used to characterize material viscoelastic properties (Chaudhuri et al. 2015; Chin et al. 2011; Higgs and Ross-Murphy 1990). If a material is subjected to strain or stress inputs small enough so that its rheological functions do not depend on the input level, the material response is said to be within the linear viscoelastic range (LVR).
Another popular method to characterize material viscoelastic behavior is through dynamic mechanical analysis (DMA), based on applying a small amplitude cyclic strain (or stress) input on a sample and measuring the resultant cyclic stress (or strain) response (Gabler et al. 2009; Kiss et al. 2004; Soong et al. 2006). For a given sinusoidal strain input the resulting stress response will be sinusoidal if the applied strain is small enough so that the tissue can be approximated as linearly viscoelastic. Viscoelastic material response is characterized by a phase lag (\(\delta\)) between the strain input and the stress response, which is comprised between 0° (purely elastic) and 90° (purely viscous). The dynamic mechanical properties are quantified using the complex modulus (\(E^{*}\)) which can be thought of as an overall resistance to deformation under dynamic loading. The complex modulus is composed of the storage (\(E'\), elastic component) and the loss (\(E{''}\), viscous component) moduli, which are additive under the linear theory of viscoelasticity (\(E^{*} = E' + iE{''}\)) (Menard 2008).
However, it is well known that these viscoelastic testing methods may pose some limitations in the case of very compliant materials, such as soft tissues and hydrogels (Tirella et al. 2014). Indeed, both step-response and dynamic mechanical tests require the establishment of an initial contact between the sample and the testing apparatus to “trigger” measurements. Starting from this contact point, a given stimulus (e.g. step of deformation or force in the case of stress relaxation or creep, respectively, or cyclic stress or strain in the case of DMA) is applied to the sample under testing, then the resultant response is measured. As a consequence, force- or strain-triggered methods are likely to cause significant pre-stress on very soft samples, altering their status. Moreover, they generally require quite long measurement trials, which may result in sample deterioration during tests (Mattei et al. 2014). To address these issues, we have recently proposed the epsilon dot method (\(\dot{\varepsilon} M\)) for deriving material viscoelastic constants through rapid measurements performed at different strain rates within the LVR (Mattei et al. 2015b; Tirella et al. 2014). However, as it is based on a global multi-curve fitting with shared parameters of stress-time data acquired at different constant strain rates, the method becomes computationally expensive when a large number of strain rates and/or replicates per strain rate are considered. Here, we introduce the apparent elastic modulus strain-rate spectrum, \(E_{\mathrm{app}}(\dot{\varepsilon} )\), as a function to derive lumped parameter constants for Generalized Maxwell (GM) linear viscoelastic models from a single-curve fitting of experimental \(E_{\mathrm{app}}\) data obtained at different \(\dot{\varepsilon} \).
2 Methods
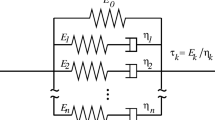
The most general form of linear viscoelastic lumped model (i.e. with constant viscoelastic parameters) is the GM model (Fig. 1) and consists of a pure spring (\(E_{0}\)) in parallel with \(N\) Maxwell arms (i.e. a spring \(E_{i}\) in series with a dashpot \(\eta_{i}\)) thus defining a set of \(N\) different characteristic relaxation times (i.e. \(\tau_{i} = \eta_{i} / E_{i}\)) (Roylance 2001).
The stress-time response of a generalized Maxwell model to a constant strain-rate input with amplitude \(\dot{\varepsilon} \) is given by
where \(N\) is the number of spring-dashpot Maxwell elements in parallel to the spring \(E_{0}\) (Tirella et al. 2014).
Since \(\partial\varepsilon/ \partial t = \dot{\varepsilon} \) is constant, \(t = \varepsilon/ \dot{\varepsilon} \) can be substituted in Eq. (1) obtaining the stress-strain response:
The tangent modulus (\(E_{t}\)), defined as the slope of the stress-strain curve at any specified stress or strain point (Zhang et al. 2002), is given by
which is a function of both strain (\(\varepsilon\)) and strain rate (\(\dot{\varepsilon} \)) or, dually, a function of time \(t = \varepsilon/ \dot{\varepsilon} \).
For very high (\(\dot{\varepsilon} \to\infty\)) and low (\(\dot {\varepsilon} \to0\)) strain rates, the \(E_{t}\) becomes independent of the strain and is, respectively, equal to the sum of all the spring constants present in the lumped model (namely the instantaneous modulus, \(E_{\mathrm{inst}} = E_{0} + \sum_{i = 1}^{N} E_{i}\) for \(\dot{\varepsilon} \to\infty\)), or to \(E_{0}\) (generally noted as the equilibrium modulus \(E_{\mathrm{eq}} = E_{0}\)) for \(\dot{\varepsilon} \to0\) as expected from classical viscoelastic theory (Lakes 2009).
Hence, from Eqs. (2) and (3), linear viscoelastic materials—that is materials which can be represented by linear viscoelastic models combining lumped parameters (i.e. springs and dashpots) whose elastic and viscous constants do not depend e.g. on strain or strain rate—exhibit non-linear concave-down stress-strain (or dually, stress-time) responses to a constant strain-rate input. These non-linear responses are dependent on the strain rate (i.e. the stress at a given strain increases with \(\dot{\varepsilon} \) due to viscous effects, Fig. 2) and their tangent (\(E_{t}\)) decreases non-linearly over strain (or time) from \(E_{\mathrm{inst}}\) (at \(\varepsilon,t = 0\)) to \(E_{\mathrm{eq}}\) (for \(\varepsilon,t \to\infty\)) because of the time-dependency owed to viscous relaxation phenomena. Thus, the changes in \(E_{t}\) are dependent on both the strain rate and, of course, the viscoelastic characteristics of the material tested.
Zhang et al. showed that: (i) the tangent modulus for constant strain-rate tests, \(E_{t}(t)\), is equivalent to the relaxation modulus from stress-relaxation tests, \(E(t) = \sigma(t) / \varepsilon_{0}\), where \(\sigma(t)\) is the stress measured over time in response to a step strain input \(\varepsilon_{0}\), and (ii) the plot of \(\sigma(t) / \dot{\varepsilon} \) versus \(\varepsilon(t) / \dot{\varepsilon} \), whose tangent returns \(E_{t}(t) = E(\varepsilon(t) / \dot{\varepsilon} )\), is no longer dependent on the strain rate (i.e. curves obtained at different strain rates can be merged into one) for linear viscoelasticity (Zhang et al. 2002). Note that if \(\sigma(t) / \dot{\varepsilon} \) versus \(\varepsilon(t) / \dot{\varepsilon} \) curves collected at different strain rates cannot be merged into one, the viscoelasticity of the material under testing is non-linear and the linear superposition principle cannot be applied.
If a material is known to exhibit pure linear viscoelastic behavior, then in principle the lumped constants of a given linear viscoelastic model (i.e. spring \(E_{i}\) and dashpot \(\eta_{i}\) values) can be derived by fitting the non-linear stress-strain data acquired at a single constant strain-rate to Eq. (2). The strain-range considered in the fitting should extend up to the region in which the stress-strain tangent (\(E_{t}\)) becomes independent of the strain in order to ensure that all the viscoelastic relaxation phenomena have occurred and hence are included in the fitted dataset. However, many real materials are non-linearly elastic, viscoelastic or inelastic. Thus, they generally exhibit either strain-hardening (concave up) or strain-softening (concave-down) stress-strain responses to a constant strain rate. Most biomedical materials, including soft tissues and hydrogels, exhibit concave up \(\sigma- \varepsilon\) curves (Fung 1993; Jaspers et al. 2014; De Pascalis et al. 2014; Rimmer 2011; Vena et al. 2006), a clear indication of non-linear strain-dependent behavior. As a consequence, linear viscoelastic models cannot be used to describe the material mechanics. Conversely, in the case of concave-down stress-strain curves it is almost impossible to determine a priori whether the non-linear behavior observed comes from linear viscoelastic phenomena or non-linear material characteristics.
As discussed above, viscoelastic materials do not exhibit an initial linear portion on their \(\sigma- \varepsilon\) curve to calculate a Young’s modulus. Nonetheless, from an engineering point of view, they are often treated as linearly viscoelastic in the region of small deformations (Mattei et al. 2014; Tirella et al. 2014; Yan and Pochan 2010). Hence, it is common practice to identify an initial linear region (called the linear viscoelastic region, LVR) for deriving an apparent (i.e. strain-rate dependent) elastic modulus (\(E_{\mathrm{app}}\)), which is independent of the magnitude of the applied strain or stress. The LVR can be considered as the first nearly lineartract of the non-linear stress-strain response exhibited by linear viscoelastic materials: within this region the material’s molecular arrangements are close to equilibrium and the mechanical response is essentially a reflection of internal dynamic processes at the molecular level (Choi et al. 2015). Since material rheological functions do not depend on the input level within the LVR, linear viscoelastic models can be reasonably employed to analyze experimental mechanical data. Depending on the testing method chosen to characterize material linear viscoelastic properties, mechanical data within LVR are typically acquired at: (i) multiple stress or strain step-input amplitudes (in the case of creep-compliance or stress-relaxation tests, respectively), (ii) constant stress or strain rate (constant-rate tests like the epsilon-dot method, \(\dot{\varepsilon} M\)), or (iii) multiple frequencies (dynamic mechanical analysis, DMA).
There is no explicit mathematical form to define the \(E_{\mathrm{app}}\) since, by definition, a linear regression procedure is required to derive the \(E_{\mathrm{app}}\) from experimental \(\sigma-\varepsilon\) data obtained at constant \(\dot{\varepsilon}\) within the LVR. However, a good approximation of the \(E_{\mathrm{app}}\) can generally be obtained by evaluating the tangent modulus (defined in Eq. (3)) at \(\varepsilon^{*} = \mbox{LVR}/2\) strain. For instance, if the LVR extends up to \(\varepsilon= 0.05\) then \(E_{\mathrm{app}} \cong \frac{\partial\sigma}{\partial\varepsilon} \vert _{\varepsilon= 0.025}\) (see Supplementary Information SI 1). Under this assumption, the \(E_{\mathrm{app}}\) epsilon dot spectrum, \(E_{\mathrm{app}} ( \dot{\varepsilon} )\), can be derived from Eq. (3), obtaining
The \(E_{\mathrm{app}} ( \dot{\varepsilon} )\) can be used to identify lumped viscoelastic parameters (i.e. \(E_{i}\), \(\eta_{i}\)) from experimental \(E_{\mathrm{app}}\) data obtained at different constant \(\dot{\varepsilon}\) as shown in Sect. 3.
3 Results
To investigate whether the \(E_{\mathrm{app}} ( \dot{\varepsilon} )\) fitting method proposed in this study returns viscoelastic constants similar to the original \(\dot{\varepsilon} M\) described in Tirella et al. (2014), it is essential to maintain all sample, testing and analysis variables unaltered: only then can results be meaningfully compared (Mattei and Ahluwalia 2016). Thus, the same apparent elastic moduli reported in Tirella et al. (2014) for both 5% w/v Type A gelatin and PDMS (10:1 base to catalyst) tested in unconfined compression at different constant strain rates (\(n=3\) replicates per strain rate) were used in this work to obtain two experimental \(E_{\mathrm{app}}\) vs. \(\dot{\varepsilon}\) datasets to analyze with the new \(E_{\mathrm{app}} ( \dot{\varepsilon} )\) fitting method. Moreover, to exclude any analysis-related variability factors other than the analysis method, the same LVR range and linear viscoelastic model previously used in Tirella et al. (2014) were used also for the \(E_{\mathrm{app}} ( \dot{\varepsilon} )\) fitting. Therefore, the \(E_{\mathrm{app}}\) vs. \(\dot{\varepsilon}\) datasets obtained from Tirella et al. (2014) were fitted to the \(E_{\mathrm{app}} ( \dot{\varepsilon} )\) function of a Maxwell Standard Linear Solid (SLS) model (Eq. (5), obtained by substituting \(N=1\) in Eq. (4)), fixing \(\varepsilon^{*} = \mbox{LVR}/2 = 0.005\).
To avoid local minima in the fitting procedure, different sets of initial guess parameter values were used for the SLS viscoelastic constants to estimate (i.e. \(E_{0}\), \(E_{1}\) and \(\eta_{1}\)). In particular, two different starting sets were defined respectively for gelatin (\(E_{0} =1\) kPa; \(E_{1} = 10\) kPa; \(\eta _{1} = 10~\mbox{kPa}\,\mbox{s}\)) and PDMS (\(E_{0} =100\) kPa; \(E_{1} = 10\) kPa; \(\eta_{1} = 100~\mbox{kPa}\,\mbox{s}\)) samples. Then an annealing scheme—multiplying and dividing each initial guess parameter value by 10—was adopted, leading to a total of 7 different initial guess sets. The minimum parameter values were constrained to zero to prevent the fitting procedure returning negative estimated viscoelastic coefficients. Comparisons between viscoelastic parameter values were made using the Student t-test, considering \(n = 3\) (i.e. the number of replicates per strain rate) and setting significance at \(p < 0.05\). The fitting procedure and the statistical analysis were implemented in OriginPro 2015 (OriginLab, USA) installed on a Dell XPS 13 9350 laptop with an Intel i7-6500U CPU, 512 GB SSD and 16 GB RAM, and running Microsoft Windows 10 Pro. Figure 3 shows experimental \(E_{\mathrm{app}}\) data and fitted curves for gelatin and PDMS samples tested in unconfined compression at different \(\dot{\varepsilon}\).
Experimental \(E_{\mathrm{app}}\) versus \(\dot{\varepsilon}\) data (squares) and respective \(E_{\mathrm{app}} ( \dot{\varepsilon} )\) fitting (dashed line) obtained for (a) gelatin and (b) PDMS samples tested in unconfined compression at different strain rates. Error bars show standard deviations of experimental data
The fitting results for Maxwell SLS models are summarized in Table 1, where \(E_{\mathrm{inst}}\) and \(E_{\mathrm{eq}}\) represent the instantaneous (i.e. \(E_{0} + E_{1}\)) and equilibrium (\(E_{0}\)) moduli, respectively, while \(\tau\) is the characteristic relaxation time, equal to \(\eta_{1} /E_{1}\). To compare the computational cost between the new \(E_{\mathrm{app}} ( \dot{\varepsilon} )\) fitting approach proposed in this study (based on a single-curve fit) and the original \(\dot{\varepsilon} M\) (based on multi-curve global fitting with shared parameters), the computation time is also shown in Table 1.
Fitting results were independent of the set of initial guess parameter values both for the \(E_{\mathrm{app}} ( \dot{\varepsilon} )\) and the \(\dot{\varepsilon} M\) method (Supplementary Information SI 2). No statically significant differences were found between the viscoelastic parameters estimated with the \(E_{\mathrm{app}} ( \dot{\varepsilon} )\) fitting and the \(\dot{\varepsilon} M\) for either gelatin or PDMS samples, demonstrating the equivalence of the two analysis methods (Table 1). Moreover, the significantly lower computational cost highlights the efficiency of the \(E_{\mathrm{app}} ( \dot{\varepsilon} )\) fitting method with respect to the original \(\dot{\varepsilon} M\).
4 Discussion
To overcome the issues of pre-stress and long experimental testing trials for viscoelastic characterization of soft materials using classical testing methods, we developed the epsilon dot method (\(\dot{\varepsilon} M\)) which is based on a series of rapid strain rate measurements (Mattei et al. 2015b; Tirella et al. 2014). However, the \(\dot{\varepsilon} M\) derivation of material viscoelastic constants involves a global multi-curve fitting of stress-time data obtained at different constant strain rates, performing chi-square minimization in a combined parameter space where viscoelastic constants to estimate are shared between the globally fitted curves (Tirella et al. 2014). As a result, this method is computationally expensive and difficult to automate when a large number of strain rates and/or replicates per strain rate are considered.
Starting from the strain-rate dependent apparent elastic modulus (\(E_{\mathrm{app}}\)) typically used for describing material viscoelastic behavior, we introduce the concept of the \(E_{\mathrm{app}}\) epsilon dot spectrum, \(E_{\mathrm{app}} ( \dot{\varepsilon} )\). This function enables the calculation of viscoelastic constants for Generalized Maxwell (GM) models through a single-curve fit of \(E_{\mathrm{app}}\) data obtained at different constant strain rate (\(\dot{\varepsilon}\)) versus \(\dot{\varepsilon}\), according to Eq. (4). The \(E_{\mathrm{app}} ( \dot{\varepsilon} )\) can be interpreted as the strain-rate domain equivalent of the storage modulus frequency spectrum, \(E ' (f)\), typical of DMA analysis.
The \(E_{\mathrm{app}} ( \dot{\varepsilon} )\) method proposed in this study was validated versus the original \(\dot{\varepsilon} M\) described in Tirella et al. (2014). As discussed in Sect. 2, unlike purely elastic materials, viscoelastic materials do not exhibit an initial linear portion on their stress-strain curve. Thus, the selection of the LVR is critical for any study dealing with viscoelastic material characterization and it is likely to affect the derived mechanical properties. According to our previous work on the \(\dot{\varepsilon} M\) (Tirella et al. 2014), we here identified the LVR as the region in which stress varies linearly with strain with \(R^{2} > 0.999\). To obtain meaningfully comparable results, two experimental \(E_{\mathrm{app}}\) vs. \(\dot{\varepsilon}\) datasets to analyze with the new \(E_{\mathrm{app}} ( \dot{\varepsilon} )\) fitting method were obtained from the same apparent elastic moduli reported in Tirella et al. (2014) for gelatin and PDMS samples. For the same reason, the \(E_{\mathrm{app}} ( \dot{\varepsilon} )\) fitting was performed considering the same LVR range (\(0 \div0.01\) strain range) and linear viscoelastic model (Maxwell SLS) previously used to derive lumped viscoelastic constants with the \(\dot{\varepsilon} M\).
Viscoelastic parameters for a Maxwell SLS model estimated using the \(E_{\mathrm{app}} ( \dot{\varepsilon} )\) equation were found to be statistically similar to those obtained with the \(\dot{\varepsilon} M\), demonstrating the equivalence of the two fitting approaches. Notably, the standard error of parameter estimations obtained with the \(E_{\mathrm{app}} ( \dot{\varepsilon} )\) fitting are slightly higher than those of the \(\dot{\varepsilon} M\), because fewer data are considered in the fitting procedure. In fact, for each experimental measurement made at a given strain rate, the former method considers only \(n=1\) representative point (i.e. \(E_{\mathrm{app}}\)) instead of the entire stress-time curve within LVR considered by the \(\dot{\varepsilon} M\).
It should be noted that, although based on a non-linear function (Eq. (4)), the \(E_{\mathrm{app}} ( \dot{\varepsilon} )\) method can only be used to characterize linear viscoelastic properties. Indeed, the \(E_{\mathrm{app}} ( \dot{\varepsilon} )\) function is non-linear only with respect to the testing input variable (i.e. the strain rate, \(\dot{\varepsilon}\)), but not to its viscoelastic parameters (i.e. spring \(E_{i}\) and dashpot \(\eta_{i}\) values), which are considered constants. This is similar to the function used to fit stress-time data in the original \(\dot{\varepsilon} M\) or to those used to fit storage and loss moduli obtained from DMA, which are both non-linear in their respective testing input variable (i.e. strain rate in the case of \(\dot{\varepsilon} M\) or frequency in the case of DMA), but constant in their viscoelastic parameters. Therefore, like \(\dot{\varepsilon} M\) and DMA, this method can only be used to analyze LVR data and describe material linear viscoelastic properties.
In conclusion, the \(E_{\mathrm{app}} ( \dot{\varepsilon} )\) fitting method presented in this work is robust and accurate and, more importantly, because a single curve is used to describe material behavior over the strain-rate spectrum, it is computationally more efficient than the original \(\dot{\varepsilon} M\) (as demonstrated by the significantly reduced computation time, Table 1). Hence it could facilitate the adoption of strain-rate mechanical testing methods and subsequent calculation of viscoelastic parameters among researchers interested in characterizing viscoelastic (bio)materials. Nano-indentation methods are particularly suited for the automated derivation of material viscoelastic properties with this approach, since they allow the acquisition of \(E_{\mathrm{app}}\) data at several strain rates in different locations of the same sample (Mattei et al. 2015b). Besides nano-indentation, it is worth noting that the \(E_{\mathrm{app}} ( \dot{\varepsilon} )\) fitting method presented in this work can be adopted to analyze LVR stress-strain data obtained from any type of constant strain-rate testing approach, regardless of the measurement length-scale, such as bulk compression (as in this work) or tension and macro-indentation. Potential applications of this viscoelastic characterization method range from mechanical and structural design for (bio)material and civil engineering (Jelen et al. 2013; Öchsner and Altenbach 2015), to tissue engineering (Mattei et al. 2017b; Tirella et al. 2015) and cell mechano-biology (Mammoto et al. 2013; Mattei et al. 2015a).
References
Chaudhuri, O., Gu, L., Darnell, M., Klumpers, D., Bencherif, S.A., Weaver, J.C., Huebsch, N., Mooney, D.J.: Substrate stress relaxation regulates cell spreading. Nat. Commun. 6, 6364 (2015). https://doi.org/10.1038/ncomms7365
Chin, H.C., Khayat, G., Quinn, T.M.: Improved characterization of cartilage mechanical properties using a combination of stress relaxation and creep. J. Biomech. 44, 198–201 (2011). https://doi.org/10.1016/j.jbiomech.2010.09.006
Choi, B., Loh, X.J., Tan, A., Loh, C.K., Ye, E., Joo, M.K., Jeong, B.: Introduction to in situ forming hydrogels for biomedical applications. Presented at the 2015
De Pascalis, R., Abrahams, I.D., Parnell, W.J.: On nonlinear viscoelastic deformations: a reappraisal of Fung’s quasi-linear viscoelastic model. Proc. Math. Phys. Eng. Sci. 470, 20140058 (2014). https://doi.org/10.1098/rspa.2014.0058
Fung, Y.C.: Biomechanics: Mechanical Properties of Living Tissues. Springer, New York (1993)
Gabler, S., Stampfl, J., Koch, T., Seidler, S., Schuller, G., Redl, H., Juras, V., Trattnig, S., Weidisch, R.: Determination of the viscoelastic properties of hydrogels based on polyethylene glycol diacrylate (PEG-DA) and human articular cartilage. Int. J. Mater. Eng. Innov. 1, 3 (2009). https://doi.org/10.1504/IJMATEI.2009.024024
Higgs, P.G., Ross-Murphy, S.B.: Creep measurements on gelatin gels. Int. J. Biol. Macromol. 12, 233–240 (1990). https://doi.org/10.1016/0141-8130(90)90002-R
Jaspers, M., Dennison, M., Mabesoone, M.F.J., MacKintosh, F.C., Rowan, A.E., Kouwer, P.H.J.: Ultra-responsive soft matter from strain-stiffening hydrogels. Nat. Commun. 5, 5808 (2014). https://doi.org/10.1038/ncomms6808
Jelen, C., Mattei, G., Montemurro, F., De Maria, C., Mattioli-Belmonte, M., Vozzi, G.: Bone scaffolds with homogeneous and discrete gradient mechanical properties. Mater. Sci. Eng. C 33, 28–36 (2013). https://doi.org/10.1016/j.msec.2012.07.046
Kiss, M.Z., Varghese, T., Hall, T.J.: Viscoelastic characterization of in vitro canine tissue. Phys. Med. Biol. 49, 4207–4218 (2004)
Lakes, R.S.: Viscoelastic Materials. Cambridge University Press, Cambridge (2009)
Mammoto, T., Mammoto, A., Ingber, D.E.: Mechanobiology and developmental control. Annu. Rev. Cell Dev. Biol. 29, 27–61 (2013). https://doi.org/10.1146/annurev-cellbio-101512-122340
Mattei, G., Ahluwalia, A.: Sample, testing and analysis variables affecting liver mechanical properties: a review. Acta Biomater. 45, 60–71 (2016). https://doi.org/10.1016/j.actbio.2016.08.055
Mattei, G., Tirella, A., Gallone, G., Ahluwalia, A.: Viscoelastic characterisation of pig liver in unconfined compression. J. Biomech. 47, 2641–2646 (2014). https://doi.org/10.1016/j.jbiomech.2014.05.017
Mattei, G., Ferretti, C., Tirella, A., Ahluwalia, A., Mattioli-Belmonte, M.: Decoupling the role of stiffness from other hydroxyapatite signalling cues in periosteal derived stem cell differentiation. Sci. Rep. 5, 10778 (2015a). https://doi.org/10.1038/srep10778
Mattei, G., Gruca, G., Rijnveld, N., Ahluwalia, A.: The nano-epsilon dot method for strain rate viscoelastic characterisation of soft biomaterials by spherical nano-indentation. J. Mech. Behav. Biomed. Mater. 50, 150–159 (2015b). https://doi.org/10.1016/j.jmbbm.2015.06.015
Mattei, G., Cacopardo, L., Ahluwalia, A.: Micro-mechanical viscoelastic properties of crosslinked hydrogels using the nano-epsilon dot method. Materials 10, 889 (2017a). https://doi.org/10.3390/ma10080889
Mattei, G., Magliaro, C., Giusti, S., Ramachandran, S.D., Heinz, S., Braspenning, J., Ahluwalia, A.: On the adhesion-cohesion balance and oxygen consumption characteristics of liver organoids. PLoS ONE 12, e0173206 (2017b). https://doi.org/10.1371/journal.pone.0173206
Menard, K.P.: Dynamic Mechanical Analysis: A Practical Introduction. CRC Press, Boca Raton (2008)
Öchsner, A., Altenbach, H.: Mechanical and Materials Engineering of Modern Structure and Component Design. Springer, Cham (2015)
Oyen, M.L.: Mechanical characterisation of hydrogel materials. Int. Mater. Rev. 59, 44–59 (2013). https://doi.org/10.1179/1743280413Y.0000000022
Rimmer, S.: Biomedical Hydrogels: Biochemistry, Manufacture and Medical Applications. Elsevier, Amsterdam (2011)
Roylance, D.: Engineering Viscoelasticity, vol. 2139, pp. 1–37. Dep. Mater. Sci. Eng. Inst. Technol., Cambridge (2001)
Soong, S.Y., Cohen, R.E., Boyce, M.C., Mulliken, A.D.: Rate-dependent deformation behavior of POSS-filled and plasticized poly(vinyl chloride). Macromolecules 39, 2900–2908 (2006). https://doi.org/10.1021/ma052736s
Tirella, A., Mattei, G., Ahluwalia, A.: Strain rate viscoelastic analysis of soft and highly hydrated biomaterials. J. Biomed. Mater. Res., Part A 102, 3352–3360 (2014). https://doi.org/10.1002/jbm.a.34914
Tirella, A., La Marca, M., Brace, L.-A., Mattei, G., Aylott, J.W., Ahluwalia, A.: Nano-in-micro self-reporting hydrogel constructs. J. Biomed. Nanotechnol. 11, 1451–1460 (2015). https://doi.org/10.1166/jbn.2015.2085
Vena, P., Gastaldi, D., Contro, R.: A constituent-based model for the nonlinear viscoelastic behavior of ligaments. J. Biomech. Eng. 128, 449–457 (2006). https://doi.org/10.1115/1.2187046
Yan, C., Pochan, D.J.: Rheological properties of peptide-based hydrogels for biomedical and other applications. Chem. Soc. Rev. 39, 3528–3540 (2010). https://doi.org/10.1039/b919449p
Zhang, X.R.R., Pang, J.H.L.H.L., Shi, X.Q.Q., Wang, Z.P.P.: On the moduli of viscoelastic materials. In: 4th Electron. Packag. Technol. Conf. 2002. 639798, pp. 318–322 (2002). https://doi.org/10.1109/EPTC.2002.1185690
Zhao, X., Huebsch, N., Mooney, D.J., Suo, Z.: Stress-relaxation behavior in gels with ionic and covalent crosslinks. J. Appl. Phys. 107, 63509 (2010). https://doi.org/10.1063/1.3343265
Acknowledgements
The work leading to these results has received funding from the European Union’s Seventh Framework Programme (FP7/2007-2013) under grant agreement no. 304961 (ReLiver), from the European Union’s Horizon 2020 research and innovation programme under the Marie Sklodowska-Curie grant agreement No 705296 (ENDYVE), and from the PRA_2016_56 of the University of Pisa.
Author information
Authors and Affiliations
Corresponding author
Electronic Supplementary Material
Below is the link to the electronic supplementary material.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Mattei, G., Ahluwalia, A. A new analytical method for estimating lumped parameter constants of linear viscoelastic models from strain rate tests. Mech Time-Depend Mater 23, 327–335 (2019). https://doi.org/10.1007/s11043-018-9385-0
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11043-018-9385-0