Abstract
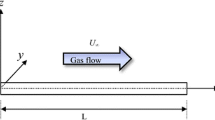
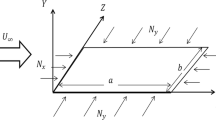
Using linear model, the parametric sensitivity analysis of viscoelastic panel flutter with an arbitrary function of relaxation, is examined by the Laplace integral transform method. The critical values of free stream velocities and frequencies of vibrations are determined from the condition that the real parts of the poles of integrand must be zero, which correspond to harmonic motion. Approximate and exact values of critical speed and corresponding frequencies for a general isotropic viscoelastic constitutive relations are obtained. The solutions are analyzed for critical, subcritical and supercritical cases. It is shown that the viscoelastic flutter speed is smaller than the corresponding elastic one if elastic moduli of material is equal to the initial value of relaxation function. Influence of aerodynamical damper is studied assuming that the parameter of viscous property of material is small enough in comparison with the parameter of aerodynamical damper and vice versa.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
Algazin, S.D., Kiyko, I.A.: About a flutter of a plate. Dokladı Akademii Nauk 383(3), 343–345 (2002) (in Russian)
Beldica, C.E., Hilton, H.H., Kubair, D.: Viscoelastic panel flutter — stability, probabilities of failure and survival times. AIAA Paper (2001–1647)
Beldica, C.E., Hilton, H.H.: Piezoelectric and damping control of divergence and flutter of viscoelastic wings-analysis and computational simulations. In: 24th dayton-cincinnati aerospace science symposium. Dayton, April (1999)
Christensen, R.M.: Theory of viscoelasticity (An introduction). Academic Press (1971)
Hilton, H.H., Beldica, C.E.: Torsion-bending flutter of viscoelastic wings. Aeronautical and Astronautical Engineering, Summery of Engineering Research (2000)
Hilton, H.H.: Implications and constraints of time independent Poisson ratios in linear isotropic and anisotropic viscoelasticity. J. Elasticity 63, 221–251 (2001)
Hilton, H.H.: Pitching instability of rigid lifting surfaces on viscoelastic supports in subsonic or supersonic potential flow. Adv. Solid Mech. 1–19 (1957), Edward Bros., Ann Arbor
Hilton, H.H., Vail, C.F.: Bending-torsion flutter of linear viscoelastic winds including structural damping. AIAA Paper 3, 1461–1481 (1993–1475)
Hilton, H.H., Yi, S.: The significance of anisotropic viscoelastic Poisson ratio stress and time dependencies. Int. J. Solids Struct. 35, 3081–3095 (1998)
Iliushin, A.A., Pobedrya, B.E.: The mathematical foundation of thermoviscoelastic theory. Nauka (1970) (in Russian)
Ilyasov, M.H., Aköz, Y.A.: The vibration and dynamic stability of viscoelastic plates. Int. J. Eng. Sci. 38, 695–714 (2000)
Kiyko, I.A., Pokazeev, V.V.: Vibrations and stability of viscoelastic strip under a gas stream. Dokladı, Akademii Nauk 401(3), 342–344 (2005) (in Russian)
Matyash, V.I.: Flutter of elasto-viscouse plate. Mech. Polim. 6, 1077–1083 (1971) (in Russian).
Tschoegl, N.W., Knauss, W.G., Emri, I.: Poisson's ratio in linear viscoelasticity — a critical review. Mech. Time-Dependent Mater. 6, 3–51 (2002)
Author information
Authors and Affiliations
Corresponding author
Additional information
AMS subject classification: 74H10, 74H55, 74K20
Rights and permissions
About this article
Cite this article
Ilyasov, M.H., Ilyasova, N.M. Flutter of viscoelastic strips. Mech Time-Depend Mater 10, 201–213 (2006). https://doi.org/10.1007/s11043-006-9018-x
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11043-006-9018-x