Abstract
Active Shape Model (ASM) has been successfully applied in the segmentation of Diffusion Tensor Magnetic Resonance Image (DT-MRI, referred to as DTI) of brain. However, due to multiple anatomical structure types, irregular shapes, small gray-scale and large amount of these images, perfect segmentation performance could not be achieved. Especially, it is sensitive to initial values with high computational complexity. In this paper, we introduce the gray information of multiple atlases and the prior information of target shapes into the ASM and propose the Multi-Atlas Active Shape Model (referred to as MA-ASM) approach for DTI segmentation. It was evaluated in a manually labeled database with 7 Region of Interest (ROI)s for each of 20 subjects. In comparison with the state of art method of STAPLE (Simultaneous Truth Performance Level Estimation), the proposed algorithm was closer to the manual segmentation shape by subjective visual effects, and had higher overlap rates and lower error detection rates on quantitative analysis than STAPLE.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Avoid common mistakes on your manuscript.
1 Introduction
The medical image segmentation is an important field for diagnosing and analyzing neurological and mental diseases, which are usually related to the abnormal fiber bundles of brain White Matter (WM). Diffusion Tensor Magnetic Resonance Imaging (DT-MRI, referred to as DTI) is a new Magnetic Resonance Imaging (MRI) technology, which can obtain the information of tissue fiber structures by measuring the different diffusion of water molecules caused by different tissue structures in body [35]. Segmentation of WM fiber bundle in DTI image plays a vital role for the diagnosis.
All DTI segmentation algorithms mainly belong to three categories: manual segmentation, segmentation with prior knowledge of image, and segmentation without prior knowledge of image, such as the similarity and topological consistency of the same tissues among different individuals. Nowadays, manual segmentation method is the gold standard for medical image segmentation. But it takes more time, and extremely depends on the experts’ experience and subjectivity, and the process has no repeat ability [27].
Segmentation without image prior knowledge refers to directly segment the DTI by utilizing underlying data information, i.e. the grey level. Because each voxel of DTI data is a tensor represented as a 3 × 3 matrix (i.e. the DTI data is 4D data), there are two ways to segment the DTI data. The first one is directly segmenting the DTI data by tensor value, and the second one is converting tensor to scalar, and then to segment scalar data to achieve the segmentation. For the first way, some works are proved to be efficient, such as tensor splines [2], classification trees [39] and watershed-based methods [12]. These methods use the direction and similarity information of tensors that makes the complexity of algorithms increased. Due to a lot of data in the clinical practice, this way is very complicated and time-consuming. For the second way, the tensor is transformed to scalar value, such as FA (fractional anisotropy) value, ADC (apparent diffusion coefficient) value. There are a lot of algorithms for segmenting scalar value, for example threshold segmentation[23], region growing method [21], level set method [13], Markov random field based segmentation and graph cut based segmentation algorithms [3, 18, 24, 37]. Threshold segmentation is simple and fast. But it does not take the spatial information into account, and is also sensitive to noise and in homogeneity. Region growing method has good robustness and fast speed, but it needs human-computer interaction to select seed pixels and also sensitive to noise. Level set method is easy to program, and its calculation is stable, but it is sensitive to the parameter selection, and easily stuck in local minima. Markov random filed and graph cut also directly segment the DTI data with good results. Due to DTI’s multiple anatomical structure types, irregular shapes, small gray-scale and large amount of data, the above segmentation methods cannot achieve perfect segmentation results by only utilizing underlying data information (i.e. the grey information). In addition, these methods have higher algorithm complexity, and are difficult to adapt to the specificity of different data.
The segmentation with a prior knowledge of image mainly includes classification based, deformable model based and multi-atlas based ones [1]. Classification based segmentation algorithms, especially convolutional neural networks (CNN), are the popular methods for segmentation in recent years due to their outstanding accuracy in computer vision tasks and trivial adaptation of models across different domains [1]. Example classification techniques have employed k-NN [25], Naive Bayes [30], Random Forest [34], SVM classifiers [28] and more recently CNN [26]. Recently, Li et al. [17] developed a novel convolutional neural network based method to directly segment white matter tract trained on a low-resolution dataset of 9149 DTI images. This method is optimized on input, loss function and network architecture selections. However, the method can only be used for white matter tract segmentation as it needs lots of labelled data for the training. Overall, there are some shortcomings in classification techniques. For example, neural network needs a lot of parameters, learning time is very long and it may even fails to achieve the purpose of learning. Deformable model based segmentation method provides the specific representation for the boundary and the shape of the object. It can approximate the irregular curve which can be treated as a minimum energy problem, so deformable model based segmentation makes the image segmentation come down to energy function minimization problem that can be transformed into solving the partial differential equation by variation method. Kass et al. [14] first proposed Snake model based segmentation algorithm. It firstly selects an initial contour that is used to iterate, then gets an optimal segmentation boundary. This method needs high requirements for selecting an initial contour, i.e. an ideal prior contour. In addition, some other deformable models are proposed for segmentation, such as Fuzzy Object Model (FOM) [15], Active Contour Model (ACM) [16, 19, 31]. However, these models are sensitive to initial values, too dependent on the choice of weight parameters, and have high computational complexity. Therefore, how to express the models more efficiently is still a problem to be further studied and solved [33]. Multi-Atlas based approaches are methods that segment the image based on the labels of aligned atlases. Multi-Atlas techniques combine the label votes from different atlases [10, 29]. Different voting schemes have been proposed that weight the contribution of each atlas according to the similarity of the atlas image to the unseen image [36], The most popular Multi-Atlas method is called Simultaneous Truth Performance Level Estimation (STAPLE) [36] that can automatically assign weights to the deformed ROIs according to the quality of data in the training set, and then fuses the deformed Region of Interest (ROI)s with EM method. Lu et al. [22] used STAPLE method for brain white matter segmentation. The multi-atlas segmentation method uses the prior information to segment the image and it is robust. In other words, it has good adaptability to the segmentation image, thus reducing the dependence on the specific image. The shortcomings of this method s that it cannot adapt the models to complex shapes.
Active Shape Model (ASM) is a method of feature points extraction based on statistical learning model. It is a variable model, which overcomes the shortcomings of previous rigid body models and adapts well to complex shape target positioning and has good adaptability. Furthermore, it is a parameterized model. By changing the parameters, a tolerable shape can be generated and the shape specificity is maintained. Therefore, in this paper, a Multi-Atlas Active Shape Model (MA-ASM) based segmentation method is proposed for DTI that combine the advantages of multi-atlas and ASM together. We first carry out multi-atlas registration. Each atlas is firstly warped to the image to be segmented, thus the deformation fields are obtained. Then, ROIs of corresponding atlas are transferred using deformation fields to get deformed ROIs. Then the method takes the deformed ROIs of multiple subjects labeled by experts in the multiple atlases as the training set, and marks the feature points which can express the targets area boundaries in these areas. And the statistical shape model is established. When searching target area in the image to be segmented, the adjustments of feature points are calculated, and the shape and pose parameters are updated. This process is repeated until the shape contour is no longer changed. Finally, the optimal segmentation result is obtained, which can obtain the boundary of segmentation result flexibly and effectively by introducing the prior multi-atlas shape information into Active Shape Model. The main contributions of the paper are the followings:
We proposed a new MA-ASM based segmentation method that adopts the prior shape information of target area, and introduces prior multi-atlas shape information to the ASM, which can combine the advantages of multi-atlas and deformed model together.
We use the manually segmented ROIs as prior information, carries out statistical analysis and establishes statistical shape model, which simplifies the calculation of the algorithm.
The new method can make full use of the gray-level information of the image to establish a local model, and combine the shape model to make the segmentation result more accurate.
2 Proposed MA-ASM algorithm
2.1 The flow of MA-ASM algorithm
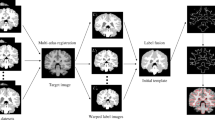
The specific flowchart of MA-ASM is shown in Fig. 1. Firstly, we use multi-atlas registration to get the training data. And then the training data is spatially normalized, and statistically analyzed with PCA method to establish an ASM and local gray model. Secondly, the initial shape of input image to be segmented is put into ASM and carried out initial spatial orientation. Thus, the new shape contour and spatial location are constantly obtained by iteratively searching in point distribution model. Then, the position, orientation and scale of the shape contour are adjusted by using pose and shape parameters, and the new shape contour is obtained at the same time. Finally, it estimates whether the shape change of adjacent iterative processes is convergent. If it does not converge, the iteratively searching procedure will continue with loop iteration until no significant shape change occurs. If the change converges, the shape contour obtained after the last iteration is the target shape and also the segmentation result.
2.2 Establishment of MA-ASM
The establishment of MA-ASM includes three steps: feature point calibration, training data alignment and the establishment of statistical model.
2.2.1 Feature point calibration
The MA-ASM firstly needs to perform the statistical analysis for the shape contour of the training data. During the statistical analysis, the same number of feature points can be calibrated on the training images manually or automatically. The shape contour can be reflected by these feature points. For the same feature points in different images of training data, the gray-scale distribution around them should be similar. Through the global statistics and analysis, the statistical model of the grey-level structure can be obtained, called grey-level model [5]. When the boundary points are used to describe the objects’ contours with similar shape, the quality of demarcated boundary points should be invariant under some transformation. In general process of calibrating feature points, the points that can effectively represent the target contour are usually selected as feature points, such as the T-connection points between boundaries and corner points that has high curvature in the shape contour. Moreover, the method of uniform equidistant sampling can be used to supplement intermediate boundary points between the feature points that describe the object’s contour. All of these marked points constitute the calibration points of the training shape contour (see Fig. 2). And the feature points must be calibrated for each training data.
When the training image is a two-dimensional image, the spatial position of the calibrated feature points could be represented by two-dimensional coordination. In this way, the set of boundary points can be represented by a vector X with the length of 2M, M is the number of feature points:
L training images with the same target are selected. The training sample set Q is obtained, where Q = X1,X2,⋯ ,XL. Because of the differences in the shape contours and the space positions between different training sets, the training sample set Q needs to be spatially normalized to carry on further statistical analysis.
Since the shape information that the demarcated boundary points of training data contain should be invariant from one shape contour to another, we choose 3D shape context method [32] here. It is further combined with Iterative Closest Point (ICP) method [8] to establish the point corresponding relationship between the shape contours.
2.2.2 Training data alignment
The labeling of ROIs on WM fiber bundles are finished with the guidance of the hospital experts, but it is not rigorous to establish the statistical model directly for these ROIs because of the differences in positions of ROIs between images with different sizes. It cannot accurately reflect the distinction among these ROIs’ contours either. Therefore, it is necessary to carry out the spatial standardization for ROIs firstly to overcome the adverse effects of ROI spatial inconsistency. Then, a geometric statistical model can be established, which can reflect the rule of changes in shape. Based on the fact that the shape contour of the target is not changed, the spatial normalization is used to make the shape contours of the images in the training sample set Q be as identical as possible.
Here, spatial normalization of the shape is performed by Procrustes Analysis [9]. By minimizing the weighted sum between the points of different shapes and the corresponding points on the average shape, the ASM can achieve the shape optimization.
Our process of spatial normalization for the training set with the size of L is divided into 3 steps as shown in Fig. 3.
2.2.3 Establishment of the statistical model
After standardizing the shape space of training data set, the distribution vectors of feature points can be obtained. Then, these data are performed dimension reduction analysis by using PCA [38]. The co-variance matrix of shape vectors, which is M × L dimension, is decomposed by PCA, and the relevant principal components and corresponding values of the data are obtained. This not only preserves the useful feature information in the lower order components, but also reduces the data dimension, and can effectively reduce the amount of calculation. PCA computes the main components of these data, allowing one to approximate any of the original points using a model with fewer than M parameters, and the statistical model about the training data set is established. The model can be expressed as:
where X is the statistical model, \(\bar {\mathbf {X}}\) is the average shape, P is the new standard orthogonal basis obtained by PCA, K is the shape parameter derived from the formula:
The parameter K = (k1,k2,⋯,kn)T can be regarded as the control coefficient of \(P^{\prime }\)s eigenvalues, that is, different K can draw different shape, and
where λi is the ith eigenvalue of P, n is the size of P. In this way, the deformable shape can be obtained in a certain range by adjusting the parameter K, which can be used to locate the target space and extract the feature points within a certain range.
2.3 Point distribution searching of MA-ASM
The known training sample set must contain the various forms of deformable contour in a shape contour. By means of feature point calibration of each image in training sample set, point corresponding relationship is established. Then, the shape contour is spatial normalized, and the ultimate point distribution model is obtained eventually. The next step is how to search and locate a shape contour in the point distribution model.
Here, we adopted a method from the reference [4]. At first, the initial shape contour and the spatial position of it are provided, the initial shape contour is obtained by image registration and ROI deformation with deformation filed. Secondly, the new optimum position of each feature point is obtained according to the grey-level model, and the spatial displacement. Thirdly, the pose parameters are updated according to spatial displacement, which can make the feature points as close as possible to the new position. Fourthly, when the pose parameters are updated, the change of shape parameter K also can be calculated, and the new shape contour is obtained as the initial shape contour of next iteration. Finally, the above four steps are to complete one iteration. When the deformation value of the two iteration shape is large, it is considered that it is not convergent and repeat the above steps to optimize the pose parameters and shape parameter K. Otherwise, it is considered to be convergent and the iteration is terminated. By means of iterative search, the ultimate segmentation results are obtained.
2.4 Point distribution searching of MA-ASM
The number of feature points is an import factor that influences the efficiency of image search. In ASM model, more feature points are marked, the boundary expression of the target area is more accurate. However, small number of feature points can reduce the computation complexity and improve the running efficiency. In order to solve the contradiction, we choose ASM under multi-resolution search framework that was proposed in [7, 11]. In this method, the position of the target contour in the image with low resolution is roughly determined firstly. Then, the precise positioning in images with higher resolutions is got by performing Gaussian pyramid. This multi-resolution search strategy not only improves the speed of the algorithm, but also avoids the problem that the shape contour converges to local optimal solution in the process of searching [6].
In the multi-resolution ASM, firstly Gauss filter is used for the shape contour images, then the filtered images are interval sampled. It will produce a series of images of Pyramid, and the resolution of these images gradually reduced. The image resolution at the second level is half of that at the previous level. In the search stage of ASM, the step length at level i + 1 in such pyramid is twice of that at level i. Therefore, large movements can be allowed to search at the coarse resolutions, and the location of the updated feature points can be found more quickly. Thus, the efficiency of the algorithm can be greatly improved by the multi-resolution search strategy.
3 Experiments and evaluations
3.1 Material
The DTI data in our experiments were from the Hammersmith Hospital of London, UK. DTI related parameters are as following: repetition time = 11894.438476 ms, echo time = 51.0 ms, reconstruction diameter = 224.0 mm, flip angle = 90.0∘ The spatial resolution of the image is 1.7409 × 1.7355 × 1.9806 mm3, resulting in volume data for head of 128 × 128 × 64 voxels. Diffusion weighted images (DWIs) are acquired along 15 unique gradient directions with b = 1000s/mm2. The age range of the data is 30 to 63 years old. Additional imaging parameters can be found at the website http://www.brain-development.org.
The DTI data are obtained by fusing DWIs from 15 diffusion gradient directions, this fusion process can be completed by FMRIB Software Library (FSL). The detailed steps can be referred to the website http://www.nitrc.org/projects/fsl.
3.2 ROIs labeling
According to the need of segmentation, the ROIs to be segmented were labeled on the subject data. Because the boundary of DTI data is not clear, and FA image can well reflect the distribution of brain white matter, the DTI data was converted into FA images firstly, and then ROIs were labeled on FA images as shown in Fig. 4. These ROIs were labeled with the guidance of the hospital experts, so the results of manual segmentation are of high accuracy and can be used as the gold standard for our experiments. In our experiments, the ROIs are the knee of the Corpus Callosum (Genu of the corpus callosum, namely Genu), the splenium of the Corpus Callosum (namely Splenium), the left and right Thalamic radiations (Anterior Thalamic Radiations, namely ATR), the left and right cortical/ corticospinal tracts of the medulla oblongata (Corticospinal/Corticobulbar tracts, namely CST) and the corpus callosum (namely Callosum).
3.3 Experimental results
In total, 20 images were used to completing the experiments. With the Leave-One-Out method, each time the 19 template images were used to build the model to validate the remaining target image and the experiments were repeated 20 times. The segmentation results of Genu, Splenium, left and right ATR, left and right CST and Callosum in the same space for one subject by using MA-ASM are shown in Fig. 5.
For the STAPLE [20] atlas fusion segmentation, SyN registration algorithm was applied to realize ROI atlas registration with FA images. Then, STAPLE algorithm is applied to achieve atlas fusion, and the fusion result is taken as the final segmentation result.
The evaluation of segmentation results are done in two ways. In the first way, a subjective visual evaluation is given, which has the intuition and easily finds serious segmentation error, but at the same time, it has subjective problem. In the second way, evaluations of segmentation results based on objective measurements are given.
3.3.1 Visual subjective evaluation
The results are directly computed by using atlas fusion based STAPLE segmentation algorithm, and the proposed ASM segmentation algorithm respectively. Results of manual segmentation are also shown for the comparison, as shown in Fig. 6. In 7 rows, results of Genu, Splenium, left ATR, right ATR, left CST, right CST and Callosum were shown respectively by STAPLE, MA-ASM and manual segmentation in different columns. From these figures, it can be found that both segmentation results do not have serious segmentation error. The results of ASM segmentation algorithm are smoother and closer to manual segmentation results than the results of atlas fusion based STAPLE segmentation algorithm.
3.3.2 Evaluation based on objective measurement
Evaluation metrics include reliability, regional statistics, accuracy and so on. Accuracy refers to the degree of similarity between segmentation results and the gold standard, which is a supervised evaluation metric. Compared with other evaluation measures, accuracy is the most intuitive method to reflect the quality of the segmentation results. Therefore, the overlap rate (OR) and false detection rate (ER) are used in this paper to evaluate the accuracy of segmentation results.
The definitions of OR and ER are given in the following equations respectively:
Here s1 and s2 are voxels of manually segmentation results and segmentation results of the proposed method respectively. The segmentation is better if OR is closer to 1. Meanwhile, the segmentation result is better if ER is closer to 0. The segmentation results of both methods for the same subject are shown in Tables 1 and 2.
From the tables, it can be found that the OR values of the proposed MA-ASM based segmentation algorithm are higher, and the ER values are lower than STAPLE based segmentation algorithm. The MA-ASM based segmentation algorithm gets better segmentation results.
In addition, the experiments were repeated 20 times, and obtained the segmentation results of the same part for different subjects. Take the Callosum for example, the OR distribution of repetitive segmentation results is shown in Fig. 7. The results clearly show that the segmentation results of MA-ASM based algorithm are better than STAPLE based algorithm.
The mean and the standard deviations of OR in 7 ROIs over 20 repetitive experiments are shown in Table 3. From Table 3, it can be seen that the OR values of the proposed MA-ASM based segmentation algorithm are higher and the running stability of the proposed algorithm is better than STAPLE based algorithm.
4 Conclusion and discussion
In this paper, a new MA-ASM based DTI segmentation algorithm is proposed, which includes establishing point distribution model, PCA analysis, establishing gray-scale texture and the use of point distribution model containing gray-scale texture in the image search. The multi-resolution search strategy for promoting the efficiency of the search is also introduced. Further, the MA-ASM is applied in the segmentation of DTI data for the experiments.
Because the atlas based segmentation and deformable model based segmentation can fully utilize the prior knowledge of image, both of them have good robustness. And the related studies show that both methods have good segmentation results. So the results of MA-ASM based DTI segmentation algorithm proposed in this paper is only compared to the results of multi-atlas based segmentation using STAPLE. Experiment results on DTI images suggest that the proposed algorithm outperforms STAPLE based algorithm and it has higher precision and better robustness compared to STAPLE based algorithm.
A few things needs to be further addressed for MA-ASM based DTI segmentation algorithm: (1) when the MA-ASM algorithm is in the process of feature point calibration, manual calibration method is tedious and time-consuming, while automatic calibration algorithm has poor extensibility, which just calibrates on similar shape. So feature point calibration algorithm can be improved; (2) when using MA-ASM model in the image search, the segmentation results can be directly influenced by initial shape contour of input image and initial space position. So more intelligent and precise initial position localization algorithm is needed; (3) MA-ASM based DTI segmentation algorithm converts the tensor data into scalar data to segment, which does not fully use the tensor information of each voxel of tensor data. So it can be improved further to the one that do not increase the calculation and fully utilize the tensor information at the same time; (4) in the medical fields, with the development of medical imaging technology and 3D visualization technology, and for meeting the rising demand of clinical diagnosis, the 3D segmentation of medical image is an important research field.
References
Antonios M, Serena JC, Danielt R (2018) A review on automatic fetal and neonatal brain MRI segmentation. Neuroimage 170:231–248
Barmpoutis A, Vemuri BC, Shepherd TM, et al. (2007) Tensor splines for interpolation and approximation of DT-MRI With applications to segmentation of isolated rat hippocampi. IEEE Trans Med Imag 26(11):1537
Bazin PL, Ye C, Bogovic JA, et al. (2011) Direct segmentation of the major white matter tracts in diffusion tensor images. Neuroimage 58(2):458–468
Cootes TF, Taylor CJ (1992) Active Shape Models -smart snakes. In: BMVC, pp 266–275
Cootes TF, Taylor CJ (1994) Using grey-level models to improve Active Shape Model search. In: IAPR. IEEE, pp 63–67
Cootes TF, Taylor CJ, Lanitis A (1994) Active Shape Models: evaluation of a multi-resolution method for improving image search. In: Proc. British machine vision conference, pp 317–338
Cootes TF, Taylor CJ, Lanitis A (1994) Multi-resolution search with Active Shape Models. In: IAPR. IEEE, pp 610–612
Friedman JH, Bentley JL, Finkel RA (1977) An algorithm for finding best matchesin logarithmic expected time. ACM Trans Math Softw (TOMS) 3(3):209–226
Goodall C (1991) Procrustes methods in the statistical analysis of shape. J R Stat Soc 53(2):285–339
Heckemann RA, Hajnal JV (2006) Automatic brain MRI segmentation combining label propagationand decision fusion. NeuroImage 33(1):115–126
Hill A, Cootes TF, Taylor CJ (2010) Active shape models and the shape approximation problem. Image Vis Comput 14(8):601–607
Jalba AC, Westenberg MA, Roerdink JB (2015) Interactive segmentation and visualization of DTI data using a hierarchical watershed representation. IEEE Trans Image Process 24(3):1025–35
Jia X, Meng MQH (2014) A survey and analysis of task allocation algorithms in multi-robot systems. Neuroimage 84(1):141–158
Kass M, Witkin A, Terzopoulos D (1988) Snakes: active contour models. Int J Comput Vis 1(4):321–331
Kobashi S, Udupa JK (2013) Fuzzy connectedness image segmentation for new- born brain extraction in MR images. In: 2013 35th Annual international conference of the IEEE engineering in medicine and biology society (EMBC), pp 7136–7139
Li W, Chen L, Li W, et al. (2013) Unraveling the characteristics of microRNA regulation in the developmental and aging process of the human brain. BMC Med Genomics 6(1):1–11
Li B, Groot M, Vernooij MW, Ikram MA, Niessen WJ, Bron EE (2018) Reproducible white matter tract segmentation using 3D U-net on a large-scale DTI Dataset. In: International workshop on machine learning in medical imaging, machine learning in medical imaging LNCS, vol 11046, pp 205–213
Liang L, Rehm K, Woods RP, et al. (2007) Automatic segmentation of left and right cerebral hemispheres from MRI brain volumes using the graph cuts algorithm. Neuroimage 34(3):1160–1170
Lim SJ, Ho YS (2006) 3-D active shape image segmentation using a scale model. In: ISSPIT. IEEE, pp 168–173
Liu T, Li H, Wong K, et al. (2007) Brain tissue segmentation based on DTI data. Neuroimage 38(1):114–123
Lu Y, Jiang T, Zang Y (2003) Region growing method for the analysis of functional MRI data. Neuroimage 20(1):455–465
Lu M, Miao CS, Wang LJ (2012) A new method of brain white matter segmentation. J Northeastern Univ 33(5):645–648. (Chinese)
Manikandan S, Ramar K, Iruthayarajan MW, et al. (2014) Multilevel thresholding for segmentation of medical brain images using real coded genetic algorithm. Measurement 47(1):558–568
Min HB, Pan R, Wu T, et al. (2009) Automated segmentation of mouse brain images using extended MRF. Neuroimage 46(3):717–725
Moeskops P, Benders, Chit MJNL, et al. (2015) Automatic segmentation of MR brain images of preterm infants using supervised classification. Neuroimage 118:628–641
Moeskops P, Viergever MA, et al. (2016) Automatic segmentation of MR brain images with a convolutional neural network. IEEE Trans Med Imaging 35:1252–1261
Pipitone J, Park MT, Winterburn J, et al. (2014) Multi-atlas segmentation of the whole hippocampus and subfields using multiple automatically generated templates. Neuroimage. 101(101):494
Sanroma G, Benkarim OM, et al. (2016) Building an ensemble of complementary segmentation methods by exploiting probabilistic estimates. Mach Learn Med Imag, 27–35
Sanroma G, Benkarim OM, Piella G (2016) Building an ensemble of complementary segmentation methods by exploiting probabilisticestimates. Mach Learn Med Imag, 27–35
Serag A, Blesa M (2016) Accurate learning with few atlases (ALFA): an algorithm for MRI neonatal brain extraction and comparison with 11 publicly available methods. Sci Rep 6:23470
Shao XX, Lin XM et al (2015) Liver DTI image segmentation method based on active contour model, CN, 104361597A[P]. (Chinese)
Shi Y, Thompson PM, Zubicaray GID, et al. (2007) Direct mapping of hippocampal surfaces with intrinsic shape context. Neuroimage 37(3):792
Wang XH, Fang LL (2013) Survey of image segmention based on active contour model. Pattern Recogn Artif Intell 26(8):751–760. (Chinese)
Wang L, Gao Y, et al. (2015) LINKS: learning-based multi-source IntegratioN framework for segmentation of infant brain images. Neuroimage 108:160–172
Wang Y, Yu Q, Liu Z, et al. (2016) Evaluation on diffusion tensor image registration algorithms. Multimed Tools Appl 13:1–18
Warfield SK, Zou KH, Wells WM (2004) Simultaneous truth and performance level estimation (STAPLE): an algorithm for the validation of image segmentation. IEEE Trans Med Imag 23(7):903
Wolz R, Heckemann RA, Aljabar P, et al. (2010) Measurement of hippocampal atrophy using 4D graph-cut segmentation: application to ADNI. Neuroimage 52 (1):109–118
Woolrich M, Hunt L, Groves A, et al. (2011) MEG beamforming using Bayesian PCA for adaptive data covariance matrix regularization. Neuroimage 57(4):1466
Zimmerman-moreno G, Mayer A, Greenspan H (2008) Classification trees for fast segmentation of DTI brain fiber tracts. In: IEEE Computer society conference on computer vision and pattern recognition workshops. CVPRW’08. IEEE, pp 1–7
Acknowledgements
This work was supported by the National Key Research and Development Program of China (2016YFC0100300), National Natural Science Foundation of China (61402371), Natural Science Basic Research Plan in Shaanxi Province of China (2019JM-311), the Fundamental Research Funds for the Central Universities of China (3102018zy020).
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Wang, Y., Zhao, Y., Guo, Z. et al. Diffusion Tensor Image segmentation based on multi-atlas Active Shape Model. Multimed Tools Appl 78, 34231–34246 (2019). https://doi.org/10.1007/s11042-019-08051-9
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11042-019-08051-9