Skip to main content
SpringerLink
Log in

Image encryption based on random projection partition and chaotic system

  • Published:
Multimedia Tools and Applications Aims and scope Submit manuscript

Abstract

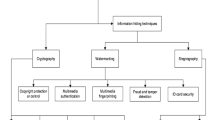
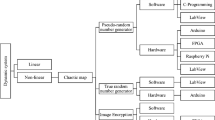
Image encryption is a useful technique of multimedia security and has been widely used in content protection, image authentication, data hiding, and so on. In this paper, we investigate the use of projection partition in image encryption, and then design an efficient image encryption algorithm based on random projection partition and chaotic system. Specifically, our algorithm randomly divides the input image into overlapping blocks. For each block, our algorithm further divides it into a set of projection lines. And then, chaotic system is exploited to generate a secret data pool. Finally, data encryption is done by random projection line swapping and XOR operation between projection line and secret sequence selected from the secret data pool. Many experiments are conducted to validate efficiency of our algorithm. Comparisons are also done and the results show that our algorithm is better than some popular algorithms.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13
Fig. 14
Fig. 15
Fig. 16
Fig. 17
Fig. 18
Fig. 19
Fig. 20

Similar content being viewed by others

References

  1. Alvarez G, Li S (2006) Some basic cryptographic requirements for chaos-based cryptosystems. Int J Bifurcation Chaos 16(8):2129–2151

    Article  MathSciNet  MATH  Google Scholar 

  2. Ginesu G, Giusto DD, Onali T (2006) Wavelet domain scrambling for image-based authentication, In: Proc. of International Conference on Acoustics, Speech, and Signal Processing (ICASSP), pp.313–316

  3. Global surveillance disclosures. Available: http://en.wikipedia.org/wiki/Global_surveillance_disclosure

  4. IEEE 754–2008 (2008) IEEE Standard for Floating-Point Arithmetic, pp.1–70

  5. Liu H, Kadir A, Niu Y (2014) Chaos-based color image block encryption scheme using S-box. AEU - Int J Electron Commun 68(7):676–686

    Article  Google Scholar 

  6. Naeem EA, Elnaby MMA, Soliman NF, Abbas AM, Faragallah OS, Semary N, Hadhoud MM, Alshibeili SA, El-Samie FEA (2014) Efficient implementation of chaotic image encryption in transform domains. J Syst Softw 97:118–127

    Article  Google Scholar 

  7. Pareek NK, Patidar V, Sud KK (2006) Image encryption using chaotic logistic map. Image Vis Comput 24(9):926–934

    Article  Google Scholar 

  8. Patidar V, Pareek NK, Purohit G, Sud KK (2011) Robust and secure chaotic standard map based pseudorandom permutation-substitution scheme for image encryption. Opt Commun 284(19):4331–4339

    Article  Google Scholar 

  9. Ping P, Xu F, Wang Z (2014) Image encryption based on non-affine and balanced cellular automata. Signal Process 105:419–429

    Article  Google Scholar 

  10. PRISM (surveillance program). Available: http://en.wikipedia.org/wiki/PRISM_(surveillance_program)

  11. Qi D (1999) Matrix transformation and its application to image hiding. J North China Univ Technol 11(1):24–28 (in Chinese)

    Google Scholar 

  12. Qin C, Wang Z, Chang CC (2012) Reversible data hiding scheme based on image inpainting. Fundam Inform 120(1):59–70

    MathSciNet  Google Scholar 

  13. Roover CD, Vleeschouwer CD, Lefebvre F, Macq B (2005) Robust video hashing based on radial projections of key frames. IEEE Trans Signal Process 53(10):4020–4036

    Article  MathSciNet  Google Scholar 

  14. Shang Z, Ren H, Zhang J (2008) A block location scrambling algorithm of digital image based on Arnold transformation, In: Proc. of the 9th International Conference for Young Computer Scientists, pp.2942–2947

  15. Sun F, Lü Z, Liu S (2010) A new cryptosystem based on spatial chaotic system. Opt Commun 283(10):2066–2073

    Article  Google Scholar 

  16. Tang Z, Dai Y, Zhang X, Zhang S (2012) Perceptual image hashing with histogram of color vector angles. The 8th International Conference on Active Media Technology (AMT 2012), December 4–7, 2012, Macau SAR, China. Lect Notes Comput Sci 7669:237–246

    Article  Google Scholar 

  17. Tang Z, Lan W, Dai Y, He J (2011) Image encryption using mapping array and random division. ICIC Express Lett, Part B: Appl 2(6):1297–1302

    Google Scholar 

  18. Tang Z, Wang S, Zhang X, Wei W (2009) Perceptual similarity metric resilient to rotation for application in robust image hashing, In: Proceedings of the 3rd International Conference on Multimedia and Ubiquitous Engineering (MUE 2009), Qingdao, China, June 4–6, 2009, pp.183–188

  19. Tang Z, Zhang X (2011) Secure image encryption without size limitation using Arnold transform and random strategies. J Multimed 6(2):202–206

    Article  Google Scholar 

  20. Tang Z, Zhang X, Huang L, Dai Y (2013) Robust image hashing using ring-based entropies. Signal Process 93(7):2061–2069

    Article  Google Scholar 

  21. Tang Z, Zhang X, Lan W (2015) Efficient image encryption with block shuffling and chaotic map. Multimed Tools Appl 74(15):5429–5448

    Article  Google Scholar 

  22. Tedmori S, Al-Najdawi N (2014) Image cryptographic algorithm based on the Haar wavelet transform. Inf Sci 269:21–34

    Article  MathSciNet  MATH  Google Scholar 

  23. The SSIM Index for image quality assessment. Available: http://www.cns.nyu.edu/~lcv/ssim/

  24. Van De Ville D, Philips W, Van de Walle R, Lemanhieu I (2004) Image scrambling without bandwidth expansion. IEEE Trans Circ Syst Video Technol 14(6):892–897

    Article  Google Scholar 

  25. Wang Z, Bovik AC, Sheikh HR, Simoncelli EP (2004) Image quality assessment: from error visibility to structural similarity. IEEE Trans Image Process 13(4):600–612

    Article  Google Scholar 

  26. Wang Q, Guo Q, Zhou J (2012) Double image encryption based on linear blend operation and random phase encoding in fractional Fourier domain. Opt Commun 285(21–22):4317–4323

    Article  Google Scholar 

  27. Wang Y, Quan C, Tay CJ (2014) Nonlinear multiple-image encryption based on mixture retrieval algorithm in Fresnel domain. Opt Commun 330:91–98

    Article  Google Scholar 

  28. Watanabe O, Nakazaki A, Kiya H (2004) A fast image-scramble method using public-key encryption allowing backward compatibility with JPEG2000, In: Proc. of International Conference on Image Processing (ICIP), pp.3435–3438

  29. Wu Y, Zhou Y, Saveriades G, Agaian S, Noonan JP (2013) Local Shannon entropy measure with statistical tests for image randomness. Inf Sci 222:323–342

    Article  MathSciNet  MATH  Google Scholar 

  30. Xiang S, Kim HJ, Huang J (2007) Histogram-based image hashing scheme robust against geometric deformations. In: Proceedings of the 9th Workshop on Multimedia & Security, ACM, New York, NY, USA, pp.121–128

  31. Xkeyscore. Available: http://en.wikipedia.org/wiki/XKeyscore

  32. Zhang G, Liu Q (2011) A novel image encryption method based on total shuffling scheme. Opt Commun 284(12):2775–2780

    Article  Google Scholar 

  33. Zhang X, Sun G, Shen L, Qin C (2014) Compression of encrypted images with multi-layer decomposition. Multimed Tools Appl 72(1):489–502

    Article  Google Scholar 

  34. Zhou Y, Cao W, Philip Chen CL (2014) Image encryption using binary bitplane. Signal Process 100:197–207

    Article  Google Scholar 

  35. Zhou Y, Panetta K, Agaian S, Philip Chen CL (2012) Image encryption using P-Fibonacci transform and decomposition. Opt Commun 285(5):594–608

    Article  Google Scholar 

  36. Zhu L, Li W, Liao L, Li H, (2006) A novel algorithm for scrambling digital image based on cat chaotic mapping, In: Proc. of International Conference on Intelligent Information Hiding and Multimedia Signal Processing (IIH-MSP), pp.601–604

  37. Zhu H, Zhao C, Zhang X (2013) A novel image encryption–compression scheme using hyper-chaos and Chinese remainder theorem. Signal Process Image Commun 28:670–680

    Article  Google Scholar 

Download references

Acknowledgments

The authors would like to thank the anonymous referees for their valuable comments and suggestions. This work is partially supported by the National Natural Science Foundation of China (61562007, 61300109, 61363034), the Guangxi Natural Science Foundation (2015GXNSFDA139040), Guangxi “Bagui Scholar” Teams for Innovation and Research, the Scientific and Technological Research Projects in Guangxi Higher Education Institutions (YB2014048), the Project of the Guangxi Key Lab of Multi-source Information Mining & Security (15-A-02-02, 14-A-02-02, 13-A-03-01), and Guangxi Collaborative Innovation Center of Multi-source Information Integration and Intelligent Processing.

Author information

Authors and Affiliations

  1. Guangxi Key Lab of Multi-source Information Mining & Security, Guangxi Normal University, Guilin, 541004, China

    Zhenjun Tang, Fei Wang & Xianquan Zhang

  2. Department of Computer Science, Guangxi Normal University, No.15 Yucai Road, Guilin, 541004, People’s Republic of China

    Zhenjun Tang, Fei Wang & Xianquan Zhang

Authors
  1. Zhenjun Tang
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Fei Wang
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Xianquan Zhang
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Zhenjun Tang.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Tang, Z., Wang, F. & Zhang, X. Image encryption based on random projection partition and chaotic system. Multimed Tools Appl 76, 8257–8283 (2017). https://doi.org/10.1007/s11042-016-3476-1

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s11042-016-3476-1

Keywords

Search

Navigation