Abstract
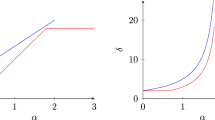
The orthant model is a directed percolation model on \(\mathbb {Z}^{d}\), in which all clusters are infinite. We prove a sharp threshold result for this model: if p is larger than the critical value above which the cluster of 0 is contained in a cone, then the shift from 0 that is required to contain the cluster of 0 in that cone is exponentially small. As a consequence, above this critical threshold, a shape theorem holds for the cluster of 0, as well as ballisticity of the random walk on this cluster.
Article PDF
Similar content being viewed by others
Avoid common mistakes on your manuscript.
References
Aizenman, M., Barsky, D.J.: Sharpness of the phase transition in percolation models. Comm. Math Phys. 108(3), 489–526 (1987)
Beekenkamp, T.: Sharp phase transitions in percolation models. In preparation (2021)
Beekenkamp, T.: Sharpness of the phase transition for the corrupted compass model on transitive graphs. Indagationes Mathematicae New Series 32 (3), 736–744 (2021)
Dereudre, D., Houdebert, P.: Sharp phase transition for the continuum Widom-Rowlinson model Annales de l’Institut Henri Poincaré. Probabilités et Statistiques 57(1), 387–407 (2021)
Duminil-Copin, H., Goswami, S., Rodriguez, P.-F., Severo, F.: Equality of critical parameters for percolation of Gaussian free field level-sets. arXiv:2002.07735 (2020)
Duminil-Copin, H., Raoufi, A., Tassion, V.: Exponential decay of connection probabilities for subcritical Voronoi percolation in \(\mathbb {R}^{d}\). Probab. Theory Relat. Fields, 1–12 (2017)
Duminil-Copin, H., Raoufi, A., Tassion, V.: Sharp phase transition for the random-cluster and Potts models via decision trees. Ann. Math. 189(1), 75–99 (2019)
Duminil-Copin, H., Raoufi, A., Tassion, V.: Subcritical phase of d-dimensional poisson–boolean percolation and its vacant set. Annales Henri Lebesgue 3, 677–700 (2020)
Grimmett, G.: Percolation, volume 321 of Grundlehren der Mathematischen Wissenschaften [Fundamental Principles of Mathematical Sciences], second edition. Springer, Berlin (1999)
Holmes, M., Salisbury, T.S.: Degenerate random environments. Random Structures & Algorithms 45(1), 111–137 (2014)
Holmes, M., Salisbury, T.S.: Random walks in degenerate random environments. Can. J. Math. 66(5), 1050–1077 (2014)
Holmes, M., Salisbury, T.S.: Conditions for ballisticity and invariance principle for random walk in non-elliptic random environment. Electron. J. Probab. 22, 1–18 (2017)
Holmes, M., Salisbury, T.S.: Phase transitions for degenerate random environments. ALEA 18, 707–725 (2021)
Holmes, M., Salisbury, T.S.: A shape theorem for the orthant model. The Annals of Probability 49(3), 1237–1256 (2021)
Hutchcroft, T.: New critical exponent inequalities for percolation and the random cluster model. Probability and Mathematical Physics 1(1), 147–165 (2020)
Menshikov, M.V.: Coincidence of critical points in percolation problems. Dokl. Akad. Nauk SSSR 288(6), 1308–1311 (1986)
Muirhead, S., Vanneuville, H.: The sharp phase transition for level set percolation of smooth planar Gaussian fields. Annales de l’Institut Henri Poincaré. Probabilités et Statistiques 56(2), 1358–1390 (2020)
O’Donnell, R.: Analysis of Boolean Functions. Cambridge University Press, Cambridge (2014)
O’Donnell, R., Saks, M., Schramm, O., Servedio, R.A.: Every decision tree has an influential variable. In: 46th Annual IEEE Symposium on Foundations of Computer Science, 2005, pp 31–39. IEEE (2005)
Acknowledgments
I thank Matija Pasch for insightful discussions on the topic, as well as for useful comments on the manuscript.
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Beekenkamp, T. Sharpness of the Phase Transition for the Orthant Model. Math Phys Anal Geom 24, 36 (2021). https://doi.org/10.1007/s11040-021-09408-z
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s11040-021-09408-z