Decentralised Functional Signatures

Abstract

With the rapid development of the Internet of Things (IoT) a lot of critical information is shared however without having guarantees about the origin and integrity of the information. Digital signatures can provide important integrity guarantees to prevent illegal users from getting access to private and sensitive data in various IoT applications. Functional signatures, introduced by Boyle, Goldwasser and Ivan (PKC 2014) as signatures with a finegrained access control, allow an authority to generate signing keys corresponding to various functions such that a user with a signing key for a function f, can sign the image of the function f on a message mi.e., can sign f(m). Okamoto and Takashima (PKC 2013) firstly proposed the notion of a decentralized multi-authority functional signature (DMA-FS) scheme, which supports non-monotone access structures combined with inner-product relations. In this paper, we generalise the definition of DMA-FS proposed by Okamoto et al. (PKC13) for even more general policy functions, which support any polynomial-size boolean predicates other than the inner product relation and allow modifications of the original message. In our multi-authority functional signature (MAFS), there are multiple authorities and each one is able to certify a specific function and issue a corresponding functional signing key for each individual with some property, rendering them very useful in application settings such smart homes, smart cities, smart health care etc. We also provide a general transformation from a standard signature scheme to a MAFS scheme. Moreover, we present a way to build a function private MAFS from a FS without function privacy together with SNARKs.

1 Introduction

With the rapid development of the Internet of Things (IoT) in various application settings (e.g., smart homes [6, 7], smart cities [4, 8], and smart health-care [1]), ensuring the communication integrity and authenticity of information shared between IoT devices becomes a major concern, since millions of devices sense and communicate large volumes of private and sensitive data. Digital signatures is one of simplest and more reliable approaches, that can be employed to achieve the integrity and authentication properties and thus, prevent illegal users from getting access to private and sensitive data.

A digital signature on a message, originally introduced by Diffie and Hellman [5], produces information that allows the receiver to verify that the original message was indeed signed by the claimed signer (sender). Boyle, Goldwasser and Ivan [2] have recently introduced a new type of signatures, called functional signatures. In a functional signature scheme, a trusted authority holds a master secret key known only to the authority. Given a description of a function f, the authority using the master secret key can generate a functional signing key sk_f associated with the function f. Anyone that has access to the functional signing key sk_f and a message m can compute f(m) as well as a functional signature σ of f(m). Such fine-grained generation of signatures is extremely useful in multiple applications such as authentication and trust-negotiation. For instance, we can consider the case where a document (message m) has some fields to be filled in, i.e., the initial document m needs to be modified by applying a function on it f(m) and then subsequently signed. Thus, it is required to produce a signature σ that corresponds to f(m). In that case, a function f could be associated with the fields of the document that need to be filled in, as well as the type of the information (e.g., calendar date). Then, by generating a signing key sk_f for this specific function f, we can guarantee which documents have been filled in and signed by an individual.

In this paper, we go beyond standard functional signatures and we re-explore the existing concept: decentralised or multi-authority functional signatures for general policy functions, which aids for smart projects such for smart home, smart city, smart health care etc.

Decentralised functional signatures Although functional signatures (FS) are a very powerful primitive, the basic concept of FS has a serious challenge since it requires that a single authority issues for all users their secret signing keys associated with different functions. This definitely contradicts the distributed public key infrastructure that allows having multiple certification authorities with different levels of trust. When considering realistic applications of functional signatures, it is hard to imagine that a single central authority will be trusted by everyone and will manage all credentials and generate functional signing keys for different functions for all individuals. Inspired by the practical demand for the distributed trust, we explore the model for multi-authority functional signatures (MAFS).

Okamoto et al. [12] firstly proposed the concept of a decentralised multi-authority functional signature (DMA-FS) scheme, which supports non-monotone access structures combined with inner-product relations [11]. Intuitively, the non-monotone access structures combined with inner-product relations [11] supported by the DMA-FS scheme of Okamoto et al. are: for properties $\mathbf {u}:=({u}_{1},\ldots ,{u}_{N})\in \mathbb {F}^{n_{1}+\ldots +n_{N}}_{q}$, a policy function $F:= (\hat {M}, ({v}_{1},\ldots ,{v}_{N})\in \mathbb {F}^{n_{1}+\ldots +n_N}_{q})$ is the componentwise inner-product relations for property vector components, e.g., {u_i ⋅ v_i = 0 or not}_{i∈{1,…,N}} that are taken as input to a span program $\hat {M}$, and the property vector u satisfies the policy F iff the truth-value vector of ((u₁ ⋅ v₁ = 0),…,(u_N ⋅ v_N = 0)) is accepted by the span program $\hat {M}$. In their DMA-FS setting, there are multiple authorities and each authority is able to generate a secret key associated with a sort of attributes u_i, i.e., a user obtains several secret keys w.r.t. the attributes it has, u := (u₁,…,u_N), each of which is issued by corresponding authority. A user with secret keys w.r.t. the attributes u := (u₁,…,u_N) is able to sign the message iff u s.t. ((u₁ ⋅ v₁ = 0),…,(u_N ⋅ v_N = 0)) is accepted by the span program $\hat {M}$.

Contrary to Okamoto et al. [12] work, in this paper we consider whether it is possible to extend the DMA-FS with respect to even more general policy functions, which are not limited to inner-product predicates [11] but support any polynomial sized boolean predicate. Furthermore, we allow one to sign a message that is in the range of a function f, which can be considered as to make some operations on the original message first and then to sign the new resulting message.

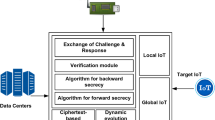
A motivating example of using MAFS in the IoT setting Before we describe our generalized multi-authority FS (MAFS) scheme in more detail, let us consider a motivating example in the IoT setting. In order to allow both businesses and customers greater visibility and tracking of their products and parcels than ever before, every shipment or parcel can be equipped with an inexpensive small device or sensor which would continuously monitor and record every information from the position of a parcel to the temperature and light conditions- meaning that those sending and receiving the parcels can see both where their items are and how they are being handled on route and whether they have been opened or not. For instance, a headphone made by a company in Germany is ordered to be delivered to China by a logistics company. A rather challenging task is keeping and updating the records of all transactions during the delivery where multiple authorities (such as country of origin, logistics company, insurance company) might be involved, while ensuring that the users are able to verify all the transactions that occurred. The concept of multi-authority functional signature properly addresses this type of problems. For example, a headphone from Country A might be ordered to be delivered to Country B by a specific logistics company X with a insurance company. The transaction messages may be updated with info about the luminous intensity and the current location of the parcel should be signed through a MAFS with a policy such that ((Original country = Country A OR B) AND (Logistics = Company X OR Y) AND (Luminous Intensity ≤ 0.2lx)). In a MAFS scheme, a user obtains several secret keys associated with multiple properties, each of which is issued by a different authority. A sensor embedded in the parcel receives a secret key (for the country of origin A) from the producer S, a secret key for the logistics company X, and a secret key for a luminous intensity from the insurance company T, where the country of origin A, the logistics company X and the insurance company T are all individual authorities.. The sensor while the parcel in on route, updates the properties information of the parcel and signs the updated messages. A user can then verify that the signed transactions (depicted in Fig. 1) indeed occurred.

Fig. 1

An example of using the multi-authority functional signature scheme in the IoT setting

Our results Our main results and contributions can be summarised as follows: (i) we introduce for the definition of multi-authority functional signatures (MAFSs) for general policy functions; (ii) we provide a general transformation from a standard signature scheme to a MAFS scheme and a corresponding construction; (iii) given a non-function-private FS scheme and a SNARK we provide a way to build a function private MAFS scheme.

In a MAFS scheme, multiple authorities can independently generate their master secret and master public verification keys. Any authority i should be able to generate a functional signing key for a user with identity UID and property U_i along with a policy F over various authorities. A user UID, with signing keys for a policy function F and different property U_i from the authority i ∈ [N], is allowed to generate a signature for the new message F(U₁,…,U_n,m) only if his property set {U_i}_{i∈ [N]} satisfies the policy, while anyone using the N authorities’ master verification keys should be able to verify the validity of the message-signature pair. An important requirement for MAFS is the security (unforgeability) against collusion attacks, which states that colluding users e.g., whose identities are UID₁ with property U₁ and UID₂ with property U₂ (even if they collude with some corrupted authorities) should not be able to forge a signature endorsed by a user UID₁ with properties U₁ and U₂. Another desirable property of MAFS is function privacy, which implies that the signature should reveal neither the function F that the functional signing key used in the signing process corresponds to, nor the message m that F was applied to. In particular, the notion of MAFS generalizes that of multi-authority attribute based signature [12].

In this paper, we first give a construction of MAFS that is not function private, based on any standard signature scheme. Then, assuming the existence of succinct non-interactive arguments of knowledge (SNARKS) for NP languages, we propose a function-private MAFS scheme from a non-function-private FS scheme. The resulting function-private MAFS scheme is defined in the common reference string model, which means that we allow all algorithms (and the adversary) to get as input also a public uniformly distributed common reference string [9, 10]. Below we describe in an informal way, highlights of our results and the approaches we employ.

Theorem 1 (Informal)

Assuming the existence of an existentially unforgeable signature scheme, then there exists a multi-authority functional signature scheme satisfying the unforgeability requirement but not function privacy.

Overview of the approach The master signing and verification key for each authority i ∈ [N] will correspond to a key pair, (msk_i,mvk_i), in an underlying (standard) signature scheme. To generate a signing key for a user with UID and property U for a function F, the authority i does the following. First, it samples a fresh signing and verification key pair (sk_i,vk_i) in the underlying signature scheme, and then signs the concatenation UID∥U∥F∥vk_i using msk_i. The signing key consists of this certificate (signature) together with sk_i. Given N signing keys, a user can sign any message m^∗ = F({(i,U_i)}_i∈[N],m) by signing m using each sk_i, and outputting these N signatures, together with N certificates of UID∥U∥F∥vk_i.

Theorem 2 (Informal)

Assuming the existence of SNARKs and a functional signature scheme that is unforgeable, then there exists a multi-authority functional signature scheme in the common reference string model satisfying the unforgeability requirement and function privacy.

Overview of the approach The setup algorithm generates a common reference string crs. The authority setup and key generation algorithms are the same as those of the construction in Theorem 2. Given N signing keys, a user does the following. First, it signs m using each $\textsf {sk}^f_{i}$, and then it generates a zero-knowledge SNARK for the following statement: ∀i ∈ [N], ∃σ_i such that σ_i is a valid signature of m^∗ = f(m) under mvk_i in the functional signature scheme. The final signature consists of the proof together with N certificates of UID∥U∥F∥vk_i.

2 Related work

Multi-authority functional encryption Inspired by the distributed trust offered by public-key encryption, Chandran et al. [3] introduced a new primitive that is called Multi-Authority Functional Encryption (MAFE) as a generalization of both Functional Encryption and Multi-Authority Attribute-Based Encryption (MA-ABE). Based on subexponentially secure indistinguishability obfuscation and injective one-way functions they show how to obtain MAFE for arbitrary polynomial-size circuits, namely $F(\{U_{id}\}_{id\in \mathcal {S}}, m)$ which is a $|\mathcal {S}|+ 1$ variate policy function (each component is in {0,1}^k) in MAFE that takes as input up to $|\mathcal {S}|$ properties and a message and outputs a value. In this paper, we generalise the definition of DMA-FS in [12] for even more general policy functions, which supports any polynomial sized boolean predicates other than the inner product relation and allows modifications of the original message. Such a generalisation is not straightforward. To achieve that we take advantage of the method that Chandran et al. [3] used to define the function policy in a multi-authority setting.

Multi-authority attribute based signature The concept of multi-authority attribute based signature (MA-ABS) was introduced by Okamoto et al. [9, 10]. In a MA-ABS model, there are multiple authorities and each authority is responsible for issuing a secret key associated with a category of attributes. But a central trustee is required in addition to multiple authorities. Okamoto et al. [12] showed that if the central authority is corrupted in MA-ABS, the security (unforgeability) of the system will be totally broken. Thus, in [12] they proposed the first MA-ABS scheme with no central authority, which supports more general predicates, non-monotone access structures in which no central authority exists and no global coordination is required except for the setting of a parameter for a prime order bilinear group and hash functions under a standard assumption, the DLIN assumption in the random oracle model. They also proposed a more general signature scheme, DMA-FS scheme, which supports non-monotone access structures combined with inner-product relations [11], and prove that the proposed DMA-FS scheme is fully secure (adaptive-predicate unforgeable and perfect private in the DMA security model) under the DLIN assumption in the random oracle model.

From the point of view of the class of functions that multi-authority FS supports, the DMA-FS scheme proposed by Okamoto et al. [12] is a special case of our generalized MAFS scheme, where the underlying predicate is specialized to be the inner product relation. Okamoto et al.’s DMA-FS scheme is fully secure (adaptive-predicate unforgeable and perfect private in the DMA security model) under the DLIN assumption in the random oracle model, while our MAFS scheme is secure in the common reference string model satisfying the unforgeability requirement and function privacy. Moreover, the notion of MA-ABS proposed by Okamoto et al. [12] is a specific case of our generalized MAFS for general policy functions since the policy function in MA-ABS can be considered as the special case of our MAFS where the policy function F always outputs the message m if the properties satisfy F.

3 Preliminaries

Definition 1 (Functional signature 2)

A functional signature scheme for a message space $\mathcal {M}$, and function family $\mathcal {F}=\{f: \mathcal {D}_f \rightarrow \mathcal {M}\}$ consists of the PPT algorithms FS = (FS.Setup,FS.KeyGen,FS.Sign,FS.Verify):

• FS.Setup(1^λ) → (msk,mvk) : on input the security parameter 1^λ, the setup algorithm outputs the master signing key and the master verification key.

• FS.KeyGen(msk,f) →sk_f : on input the master signing key and a function $f\in \mathcal {F}$, the key generation algorithm outputs a signing key for f .

• FS.Sign(f,sk_f,m) → (f(m),σ) : on input the signing key for function $f\!\in \mathcal {F}$ and a message $m\in \mathcal {D}_f$, the signing algorithm outputs f(m) and a signature of f(m).

• FS.Verify(mvk,m^∗,σ) →{0,1} : on input the master verification key mvk, a message m^∗ and a signature σ, the verification algorithm outputs 1 if the signature is valid.

We require it to satisfy the following conditions:

Correctness$\forall f\in \mathcal {F}$, $\forall m\in \mathcal {D}_f$, (msk,mvk) ←FS.Setup(1^λ), (m^∗,σ) ←FS.Sign(f,sk_f,m), it holds that

$$\textsf{FS.V}\textsf{erify}(\textsf{mvk}, m^{\ast}, \sigma)= 1. $$

Unforgeability The scheme is unforgeable if the advantage of any PPT algorithm $\mathcal {A}$ in the following game is negligible:

• The challenger generates (msk,mvk) ←FS.Setup(1^λ), and gives mvk to $\mathcal {A}$;

• The adversary is allowed to query a key generation oracle O_key, and a signing oracle O_sign, that share a dictionary indexed by tuples $(f, i)\in \mathcal {F}\times \mathbb {N}$, whose entries are signing keys: $\textsf {sk}_{i}^{f}\leftarrow \textsf {FS.KeyGen}(\textsf {msk}, f)$. This dictionary keeps track of the keys that have been previously generated during the unforgeability game. The oracles are defined as follows:

  • O_key(f,i) :

    • If there exists an entry for the key (f,i) in the dictionary, then output the corresponding value, $\textsf {sk}^{i}_{f}$.

    • Otherwise, sample a fresh key $\textsf {sk}^{i}_{f} \leftarrow \textsf {FS.Key} \textsf {Gen}(\textsf {msk}, f)$, add an entry $(f, i)\rightarrow \textsf {sk}^i_f$ to the dictionary, and output $\textsf {sk}^i_f$.

  • O_sign(f,i,m) :

    • If there exists an entry for the key (f,i) in the dictionary, then generate a signature on f(m) using this key: $\sigma \leftarrow \textsf {FS.Sign}(f, \textsf {sk}^i_f, m)$.

    • Otherwise, sample a fresh key $\textsf {sk}^i_f \leftarrow \textsf {FS.Key} \textsf {Gen}(\textsf {msk}, f)$, add an entry $(f, i)\rightarrow \textsf {sk}^{i}_{f}$ to the dictionary, and generate a signature on f(m) using this key: $\sigma \leftarrow \textsf {FS.Sign}(f, \textsf {sk}^{i}_{f}, m)$.

• The adversary wins if it can produce (m^∗,σ) such that:

  • FS.Verify(mvk,m^∗,σ) = 1.

  • There exists no m such that m^∗ = f(m) for any f which was sent as a query to the O_key oracle.

  • There exists no (f,m) pair such that (f,m) was a query to the O_sign oracle and m^∗ = f(m).

Function privacy The scheme is function private if the advantage of any PPT algorithm $\mathcal {A}$ in the following game is negligible:

• The challenger honestly generates (mvk,msk) ←FS.Setup(1^λ) and gives both values to the adversary.

• The adversary $\mathcal {A}$ chooses a function f₀ and receives an (honestly generated) secret key $\textsf {sk}_{f_{0}}\leftarrow \textsf {FS.KeyGen} (\textsf {msk}, f_{1})$.

• The adversary $\mathcal {A}$ chooses a second function f₁ for which |f₀| = |f₁| and receives an (honestly generated) secret key $\textsf {sk}_{f_{1}}\leftarrow \textsf {FS.KeyGen}(\textsf {msk}, f_{1})$.

• The adversary chooses a pair of messages m₀,m₁ for which |m₀| = |m₁| and f₀(m₀) = f₁(m₁).

• The challenger selects a random bit b ←{0,1} and generates a signature on the image f₀(m₀) = f₁(m₁) using secret key $\textsf {sk}_{f_{b}}$, and gives the resulting signature $\sigma \leftarrow \textsf {Sign}(\textsf {sk}_{f_{b}}, m_{b})$ to the adversary.

• The adversary outputs a bit b^′, and wins the game if b^′ = b.

4 Multi-authority functional signature

We describe syntax and security notions of a multi-authority functional signature scheme.

Definition 2 (Multi-Authority FS (MAFS))

A decentralized multi-authority FS scheme is composed of the following algorithms:

• ASetup(id,1^λ) → (MVK_id,MSK_id) : Each authority $id\in \mathcal {I}$ runs the authority setup algorithm to generate its own public verification key and secret key pair, (MVK_id,MSK_id). The authority id publishes MVK_id and stores MSK_id.

• $\textsf {KeyGen}(\textsf {MSK}_{id}, \textsf {UID}, U, F)\rightarrow K^{\textsf {UID},U}_{id,F}:$ When an authority id who wishes to issue a user, whose identity is UID, a secret key associated with a property U and a policy function F, it runs the key generation algorithm that outputs a secret key $K^{\textsf {UID},U}_{id,F}$. The authority gives $K^{\textsf {UID},U}_{id,F}$ to the user.

• $\textsf {Sign}(\{K^{\textsf {UID},U_{id}}_{id,F}\}_{(id,U_{id})\in {\Gamma }}, m) \rightarrow$$(F(\{(id,U_{id})\}_{(id,U_{id}) \in {\Gamma }}, m),$σ) : A user signs a message m with a |Γ| + 1 < O(poly(λ)) variate policy function F (each component is in {0,1}^λ), only if the user has obtained a set of secret keys {Kid,F UID,U_id|(id,U_id) ∈Γ} from the authorities such that all properties included in Γ are satisfied by the policy function. Then, the user outputs the value $F(\{(id,U_{id})\}_{(id,U_{id})\in {\Gamma }}, m)$ and a signature of $F(\{(id,U_{id})\}_{(id,U_{id})\in {\Gamma }}, m)$. F takes as input up to |Γ| properties and a message and outputs a value.

• Verify({MVK_id}_id∈Γ,m^∗,σ) →{0,1} : To verify a signature σ on a message m^∗, using a set of public keys for relevant authorities {MVK_id}_id∈Γ, a user runs the verification algorithm which outputs a boolean value accept := 1 or reject := 0.

Definition 3 (Correctness of MAFS)

A MAFS scheme is said to be correct, if, for all $F\in \mathcal {F}$, $m\in \mathcal {D}_f$, authority $id\in \mathcal {I}$, (MVK_id,MSK_id) ←ASetup(id,1^λ) , Kid,F UID,U_id ←KeyGen(MSK_id,UID,U_id,F) assigned by the authority id for the user UID with property U_id and policy function F, and $(F(\{(id,U_{id})\}_{(id,U_{id})\in {\Gamma }}, m), \sigma ) \leftarrow \textsf {Sign}(\{K^{\textsf {UID},U_{id}}_{id,F}\}_{(id,U_{id})\in {\Gamma }}, m)$ for a set of authorities ${\Gamma }\subset \mathcal {I}$, if it satisfies the following condition:

$$\textsf{Verify}(\{\textsf{MVK}_{id}\}_{id\in {\Gamma}}, F(\{(id,U_{id})\}_{(id,U_{id})\in {\Gamma}}, m), \sigma)= 1. $$

Remark 1

• 1. We assume that each user is allowed to have only one particular property corresponding to one authority (category) id.

• 2. For |Γ| + 1 < O(poly(λ)) variate policy function F, any different component of property is associated with a different authority. In fact, a policy function F consists of a predicate Predic which is used to indicate the set of properties that are accepted or not, and a deterministic function f which is used to modify the input message. The functionality of $F(\{(id,U_{id})\}_{(id,U_{id})\in {\Gamma }}, m)$ first checks whether $\textsf {Predic}\\(\{(id,U_{id})\}\text {} _{(id,U_{id})\in {\Gamma }})= 1$, if it is true then it outputs f(m); else it outputs ⊥.

• 3. For a set of properties {(id,U_id)}_id which is accepted by F, we denote it as Γ. Since a different property component in F corresponds to different authorities, we misuse the notation id ∈Γ to represent the authority that belongs to the accepted set.

Definition 4 (Unforgeability of MAFS)

For any PPT adversary, we define $\textsf {Adv}^{\textsf {MAFS,UF}}_{\mathcal {A}}(\lambda )$ to be the success probability in the following experiment for any security parameter λ. For ease of notation let us assume the chosen set of authorities by the adversary is [N] for a polynomial N. A MAFS scheme is existentially unforgeable if the success probability of any polynomial-time adversary is negligible:

• The adversary $\mathcal {A}$ outputs [N]. The challenger runs the ASetup for the authorities labelled in [N] and hands over the verification keys of all the authorities to $\mathcal {A}$. Adversary $\mathcal {A}$ specifies a set S ⊂ [N] of corrupted authorities, and gets {MSK_i}_i∈S. Let’s denote $\bar {S} :=[N]\backslash S$.

• The adversary is allowed to query a key generation oracle O_key and a signing oracle O_sign, that share a dictionary indexed by tuples (UID,i,U_i,F), whose entries are keys: Ki,F UID,U_i ←KeyGen(MSK_i,UID,U_i,F). This dictionary keeps track of the keys that have been previously generated during the unforgeability game. The oracles are defined as follows :

  • O_key(UID,i,U_i,F) : The attacker $\mathcal {A}$ submits tuples of the form (UID,i,U_i,F) to the challenger, where UID is a user’s identity and U_i is the user’s property w.r.t a non corrupted authority i. The challenger responds by giving $\mathcal {A}$ the corresponding key Ki,F UID,U_i.

    • If there exists an entry for (UID,i,U_i,F) in the dictionary, then output the corresponding value Ki,F UID,U_i.

    • Else, generate Ki,F UID,U_i ←KeyGen(MSK_i,UID, U_i,F), add an entry (UID,i,U_i,F) → Ki,F UID,U_i to the dictionary, and output Ki,F UID,U_i.

  • $\textsf {O}_{\textsf {sign}}(\{\textsf {UID},i,U_{i},F\}\text {} _{i\in \bar {S}}, \{K^{\textsf {UID},U_{i}}_{i,F}\}\text {} _{i\in S}, m):$ The attacker selects a policy F and wishes to get the user UID’s signature.

    • For any $i \in \bar {S}$, generate Ki,F UID,U_i ←KeyGen(MSK_i,UID,U_i,F) and add the entry (UID,i, U_i,F) → Ki,F UID,U_i to the dictionary. Run Sign({Ki,F UID,U_i}_i∈[N],m) to generate a tuple (F({(i,U_i)}_i∈[N],m),σ) and return it back.

• At the end, $\mathcal {A}$ outputs (m^∗,σ^∗). We say the adversary succeeds, if

  • Verify({MVK_i}_i∈[N],m^∗,σ^∗) = 1.

  • $(\{\textsf {UID},i, U_{i}, F^{\ast }\}\text {} _{i\in \bar {S}}, \{K^{\textsf {UID},U_{i}}_{i,F^{\ast }}\}\text {} _{i\in S}, \tilde {m})$ has never been sent as a query to the oracle O_sign for any F^∗ and $\tilde {m}$ such that $m^{\ast }= F^{\ast }(\{(i,U_{i})\}\text {} _{i\in [N]}, \tilde {m})$.

  • There doesn’t exist m such that m^∗ = F^∗({(i,U_i )}_i∈[N],m) where for any $i \in \bar {S}$, (UID,i,U_i,F^∗) has been sent as a query to the oracle O_key and the user UID’s property set {(i,U_i)}_i∈[N] is accepted by F^∗.

Remark 2

Since the predicate circuit Predic contained in the policy function F^∗ is specified over N properties (i,U_i), we say that F^∗ does not accept Γ_UID which means that when the properties corresponding to any authority $i\in \bar {S}$ are taken from Γ_UID no matter what the leftover |S| properties of the user UID are, F^∗ never accepts it.

Definition 5 (Function privacy of MAFS)

For any PPT adversary, we define $\textsf {Adv}^{\textsf {MAFS,priv}}_{\mathcal {A}}(\lambda )$ to be the success probability in the following experiment for any security parameter λ. A MAFS scheme is function private if the success probability of any polynomial-time adversary is negligible:

• The adversary $\mathcal {A}$ outputs [N]. The challenger runs the setup for all N authorities labelled in [N], namely generating a key pair (MVK_i,MSK_i) ←ASetup(i,1^λ) and hands over the verification keys of all the authorities to $\mathcal {A}$. The adversary $\mathcal {A}$ specifies a set S ⊂ [N] of corrupted authorities, and gets their master secret keys {MSK_i}_i∈S. Let us denote this set of corrupted authorities as $\bar {S} :=[N]\backslash S$.

• The adversary $\mathcal {A}$ chooses a policy function F₀ as well as a tuple (UID,i,U_i,F₀) for one specific user UID and his property U_i according to the category i, and receives an (honestly generated) key $K^{\textsf {UID},U_{i}}_{i, F_{0}}\leftarrow \textsf {KeyGen}(\textsf {MSK}_{i}, \textsf {UID},U_{i}, F_{0})$ corresponding to an uncorrupted authority $i\in \bar {S}$.

• The adversary $\mathcal {A}$ chooses a second policy function F₁ for which |F₀| = |F₁|, as well as a tuple (UID,i,U_i,F₁) for the same user UID and his property U_i according to the category i, and receives an (honestly generated) secret key $K^{\textsf {UID},U_{i}}_{i,F_{1}}\leftarrow \textsf {KeyGen}(\textsf {MSK}_{i}, \textsf {UID},U_{i}, F_{1})$ corresponding to the uncorrupted authority $i\in \bar {S}$.

• The adversary chooses a pair of messages m₀,m₁ for which |m₀| = |m₁| and F₀ ({(i,U_i)}_i∈[N],m₀) = F₁ ({(i,U_i)}_i∈[N],m₁).

• The challenger selects a bit b ←{0,1} and generates a signature on the image m^′ = F₀ ({(i,U_i)}_i∈[N],m₀) = F₁ ({(i,U_i)}_i∈[N],m₁) using secret key $K^{\textsf {UID},U_{i}}_{i, F_b}$, and gives the resulting signature $\sigma \leftarrow \textsf {Sign}(\{K^{\textsf {UID},U_{i}}_{i,F_b} \}\text {} _{i\in [N]}, m_{b})$ to the adversary.

• The adversary outputs a bit b^′, and wins the game if b^′ = b.

Remark 3

The policy functions F₀ and F₁ should contain the same predicates, which means F₀ = Predic∥f₀ and F₁ = Predic∥f₁.

Definition 6 (MAFS with CRS)

We say that (ASetup, KeyGen, Sign, Verify) is a MAFS scheme with CRS if Definition 2 is satisfied except that we allow all algorithm (and the adversary) to get as input also a public uniformly distributed common random string.

5 Our construction for MAFS

5.1 MAFS from standard signatures

In this section, we provide a construction of a MAFS scheme based on any standard signature scheme (i.e., existentially unforgeable under chosen-message attacks). Our resulted MAFS scheme is proved to be unforgeable as the Definition 4, but not function private.

The main ideas of our construction are as follows. The master signing and public keys for each authority i(MSK_i,MVK_i) will simply be a standard key pair for the underlying signature scheme. The signing key generated by the authority i for a user’s identity UID, a property U and a function F consists of a fresh key pair (sk,vk) for the underlying signature scheme, and a signature (with respect to MVK_i) on the user’s identity UID, a property U and a function F together with vk. We can regard this signature as a certificate authenticating that the owner of key vk is allowed to sign values resulted from the policy function F.

Let λ denote the security parameter and N denote the bound on the number of authorities used, while signing the message. Let Sig=(Sig.Setup, Sig.Sign, Sig.V-erify) be a signature scheme that is existentially unforgeable. We propose a MAFS scheme as follows:

• ASetup(i,1^λ) : Each authority i ∈ [N] runs Sig.Setup (1 ^λ) → (msk_i,mvk_i) and sets MSK_i = msk_i and MVK_i = mvk_i.

• KeyGen(MSK_i,UID,U,F) :

  • Sample a signing and verification key pair for signature scheme (sk_i,vk_i) ←Sig.Setup(1^λ).

  • Parse MSK_i = msk_i. Run $\sigma _{\textsf {vk}_{i}}\leftarrow \textsf {Sig.Sign}$ (msk_i, UID∥U∥F∥vk_i).

  • Create a certificate $c^{\textsf {UID},U}_{i,F}=(\textsf {vk}_{i}, \sigma _{\textsf {vk}_{i}},\textsf {UID},$U,F).

  • Set $K^{\textsf {UID}, U}_{i,F}=(\textsf {sk}_{i}, c^{\textsf {UID},U}_{i,F})$ and output key $K^{\textsf {UID}, U}_{i,F}$.

• Sign({Ki,F UID,U_i}_i∈[N],m) :

  • Parse Ki,F UID,U_i = (sk_i,ci,F UID,U_i) where ci,F UID,U_i$=(\textsf {vk}_{i}, \sigma _{\textsf {vk}_{i}}, \textsf {UID}, U_{i}, F)$, and run σ_i ←Sig.Sign(sk_i,m) for all i ∈ [N].

  • Compute m^∗ = F({(i,U_i)}_i∈[N],m) and set σ = (m,{ci,F UID,U_i,σ_i}_i∈[N]).

  • Output (m^∗,σ).

  Remark 4

  When {(i,U_i)}_i∈[N] is rejected by Predic the output of the policy function F will be ⊥, and the corresponding signature should also be ⊥.

• Verify({MVK_i}_i∈[N],m^∗,σ) :

  • Parse σ = (m,{ci,F UID,U_i,σ_i}_i∈[N]) and ci,F UID,U_i$=(\textsf {vk}_{i}, \sigma _{\textsf {vk}_{i}}, \textsf {UID}, U_{i}, F)$, and perform the following checks. If all of the checks pass output 1; otherwise output 0.

    • 1. m^∗ = F({(i,U_i)}_i∈[N],m);

    • 2. Sig.Verify(vk_i,m,σ_i) = 1 for all i ∈ [N];

    • 3. $\textsf {Sig.Verify}(\textsf {mvk}_{i},\textsf {UID}\|U_{i}\|F\|\textsf {vk}_{i}, \sigma _{\textsf {vk}_{i}})= 1$ for all i ∈ [N].

Theorem 3

If the signature schemeSig is existentially unforgeable under chosen message attacks, then our multi-authority functional signature scheme asspecified above satisfies the unforgeability requirement defined in Section 4.

Proof

Let $\mathcal {A}_{\textsf {MA}}$ be a PPT adversary in the unforgeability game for multi-authority functional signatures that is allowed to make query to the oracles O_key and O_sign. Assume $\mathcal {A}_{\textsf {MA}}$ made polynomial numbers of queries, Q(λ) in total to the oracles O_key and O_sign. We construct an adversary $\mathcal {B}_{\textsf {Sig}}$ with $\mathcal {A}_{\textsf {MA}}$ as a subroutine such that, if $\mathcal {A}_{\textsf {MA}}$ wins in the unforgeability game for MAFS with non-negligible probability, then $\mathcal {B}_{\textsf {Sig}}$ breaks the unforgeability game of underlying signature scheme, which is assumed to be unforgeable.

For $\mathcal {A}_{\textsf {MA}}$ to win unforgeability game of MAFS, it should output a message signature pair $(m^{\ast },\sigma ^{\ast }=(\tilde {m}, \{ c^{\textsf {UID},U_{i}}_{i,F^{\ast }}\}\text {} _{i\in [N]}, \{\sigma ^{\ast }_{i}\}\text {} _{i\in [N]}))$ where $c^{\textsf {UID},U_{i}}_{i,F^{\ast }}=(\textsf {vk}_{i},$$\sigma _{\textsf {vk}_{i}},$ UID,U_i,F^∗) such that:

• For each $i\in \bar {S}$, $\sigma ^{\ast }_{i}$ is a valid signature of $\tilde {m}$ under the verification key vk_i;

• For each $i\in \bar {S}$, $\sigma _{\textsf {vk}_{i}}$ is a valid signature of UID∥U_i∥F∥vk_i under mvk_i;

• $m^{\ast }=F^{\ast }(\{(i,U_{i})\}\text {} _{i\in [N]}, \tilde {m})$;

• $\mathcal {A}_{\textsf {MA}}$ has not sent a query of form ({UID,i,U_i, $F^{\ast }\}\text {} _{i\in \bar {S}}, \{K^{\textsf {UID},U_{i}}_{i,F^{\ast }}\}\text {} _{i\in S}, \tilde {m})$ to the signing oracle O_sign.

• $\mathcal {A}_{\textsf {MA}}$ has not sent queries (UID,i,U_i,F^∗) for all $i \in \bar {S}$, to the oracle O_key such that the user’s UID property set {(i,U_i)}_i∈[N] is accepted by F^∗ and m^∗ is in the range of the function F^∗.

Assume there are N − 1 authorities that are corrupted, while the uncorrupted one’s identity is i^∗. There are two cases for such a forgery $\left (m^{\ast },\sigma ^{\ast }=(\tilde {m}, \{c^{\textsf {UID},U_{i^{\ast }}}_{i^{\ast },F^{\ast }},\sigma ^{\ast }_{i^{\ast }}\}, \{c^{\textsf {UID},U_{i}}_{i,F^{\ast }},\sigma ^{\ast }_{i}\}\text {} _{i\in [N]\backslash i^{\ast }})\right )$ where $c^{\textsf {UID},U_{i}}_{i,F^{\ast }}=(\textsf {vk}_{i}, \sigma _{\textsf {vk}_{i}}, \textsf {UID}, U_{i}, F^{\ast })$ for all i ∈ [N]:

• Type I forgery: The tuples $(\textsf {vk}_{i^{\ast }},\textsf {UID}, U_{i^{\ast }}, F^{\ast })$ satisfy that $\textsf {UID}\|U_{i^{\ast }}\|F^{\ast }\|\textsf {vk}_{i^{\ast }}$ has not been signed under $\textsf {mvk}_{i^{\ast }}$ for the queries of $\mathcal {A}_{\textsf {MA}}$ to both the oracle O_sign and O_key.

• Type II forgery: The tuples $(\textsf {vk}_{i^{\ast }},\textsf {UID}, U_{i^{\ast }}, F^{\ast })$ satisfy that $\textsf {UID}\|U_{i^{\ast }}\|F^{\ast }\|\textsf {vk}_{i^{\ast }}$ has been signed under $\textsf {mvk}_{i^{\ast }}$ during the queries of $\mathcal {A}_{\textsf {MA}}$ to both the oracle O_sign and O_key.

Here we assume that all the queries of $\mathcal {A}_{\textsf {MA}}$ send to the oracles O_sign are proceeded by the oracle O_key to generate a signing key as intermediate steps.

We now describe the signature adversary $\mathcal {B}_{\textsf {Sig}}$. In the unforgeability game for the standard signature scheme, given the verification key vk_Sig, and access to a signing oracle $\textsf {O}_{\textsf {Reg}_{\textsf {sig}}}$, $\mathcal {B}_{\textsf {Sig}}$ wins the unforgeability game if he successfully outputs a forgery, i.e., a signature for a message that was not queried to $\textsf {O}_{\textsf {Reg}_{\textsf {sig}}}$. In order to play the role of the challenger interacting with $\mathcal {A}_{\textsf {MA}}$ in the security game for MAFS, $\mathcal {B}_{\textsf {Sig}}$ must simulate the O_key and O_sign oracles. $\mathcal {B}_{\textsf {Sig}}$ flips a coin b, and proceeds as following.

Case 1:b= 1$\mathcal {B}_{\textsf {Sig}}$ guesses that $\mathcal {A}_{\textsf {MA}}$ will produce a Type I forgery:

First $\mathcal {B}_{\textsf {Sig}}$ sets vk_Sig as the master verification key for the authority i^∗ in the MAFS security game, namely $\textsf {mvk}_{i^{\ast }} :=\textsf {vk}_{\textsf {Sig}}$ and sends it to $\mathcal {A}_{\textsf {MA}}$. For all of the other corrupted authorities, $\mathcal {B}_{\textsf {Sig}}$ behaves honestly. To simulate the O_key and O_sign oracles, $\mathcal {B}_{\textsf {Sig}}$ maintains a dictionary indexed by the tuples $(\textsf {UID}, i^{\ast }, U_{i^{\ast }}^{j}, F)$, whose entries are signing keys that are generated by the authority i^∗ for the user UID with property $U_{i^{\ast }}^{j}$ and policy function F. $\mathcal {B}_{\textsf {Sig}}$ answers the queries issued by $\mathcal {A}_{\textsf {MA}}$ as follows:

• $\textsf {O}_{\textsf {key}}(\textsf {UID}, i^{\ast }, U_{i^{\ast }}^{j}, F):$

  • If there exists an entry for the tuple $(\textsf {UID}, i^{\ast }, U_{i^{\ast }}^{j},F)$ in the dictionary, then output the corresponding value $K^{\textsf {UID}, U_{i^{\ast }}^{j}}_{i^{\ast }, F}$.

  • Otherwise, run (sk_j,vk_j) ←Sig.Setup(1^λ) and send $\textsf {UID}\|U_{i^{\ast }}^{j}\|F\|\textsf {vk}_{j}$ to its own signing oracle to get $\sigma _{\textsf {vk}_{i^{\ast }}^{j}}\leftarrow \textsf {O}_{\textsf {Reg}_{\textsf {sig}}}(\textsf {UID}\|U_{i^{\ast }}^{j}\|F\|\textsf {vk}_{j})$. Set $K^{\textsf {UID},U_{i^{\ast }}^{j}}_{i^{\ast }, F} =(\textsf {sk}_j, c^{\textsf {UID},U_{i^{\ast }}^{j}}_{i^{\ast },F})$ where $c^{\textsf {UID},U_{i^{\ast }}^{j}}_{i^{\ast },F}=(\textsf {vk}_j, \sigma$$_{\textsf {vk}_{i^{\ast }}^{j}}, \textsf {UID}, U_{i^{\ast }}^{j}, F)$, add it to the dictionary, and output it.

• $\textsf {O}_{\textsf {sign}}(\{\textsf {UID},i^{\ast },U_{i^{\ast }},F\}, \{K^{\textsf {UID},U_{i}}_{i, F}\}\text {} _{i\in [N]\backslash i^{\ast }}, m):$

  • If there exists an entry for the tuple $\{\textsf {UID},i^{\ast },U_{i^{\ast }},$F} in the dictionary, namely the key $K^{\textsf {UID},U_{i^{\ast }}}_{i^{\ast }, F}$, then it generates (F({(i,U_i)}_i∈[N],m),σ) ←Sign({Ki,F UID,U_i}_i∈[N],m) and outputs the result.

  • Otherwise, $\mathcal {B}_{\textsf {Sig}}$ samples a new pair of key for the signature scheme, $(\textsf {sk}_{i^{\ast }}, \textsf {vk}_{i^{\ast }})\leftarrow \textsf {Sig.Setup}(1^{\lambda })$, and obtains $\sigma _{\textsf {vk}_{i^{\ast }}}\leftarrow \textsf {O}_{\textsf {Reg}_{\textsf {sig}}}$$(\textsf {UID}\|U_{i^{\ast }}\|F\|\textsf {vk}_{i^{\ast }})$ fr- om its own signing oracle. It sets $K^{\textsf {UID},U_{i^{\ast }}}_{i^{\ast }, F} :=(\textsf {sk}_{i^{\ast }}, c^{\textsf {UID},U_{i^{\ast }}}_{i^{\ast },F})$ where $c^{\textsf {UID},U_{i^{\ast }}}_{i^{\ast },F}=(\textsf {vk}_{i^{\ast }}, \sigma _{\textsf {vk}_{i^{\ast }}}, \textsf {UID}, U_{i^{\ast }}, F)$, and adds it to the dictionary. For each i ∈ [N], it then computes σ_i ←Sig.Sign(sk_i,m) and m^∗ = F({(i,U_i)}_i∈[N],m). It sets σ := (m,{ci,F UID,U_i}_i∈[N],{σ_i}_i∈[N]), then outputs (m^∗,σ).

Eventually, $\mathcal {A}_{\textsf {MA}}$ outputs a message signature forgery $\left (m^{\ast },\sigma ^{\ast }=(\tilde {m}, \{c^{\textsf {UID},U_{i^{\ast }}}_{i^{\ast },F^{\ast }}, \sigma ^{\ast }_{i^{\ast }}\},\{c^{\textsf {UID},U_{i}}_{i,F^{\ast }},\sigma ^{\ast }_{i}\}\text {} _{i\in [N]\backslash i^{\ast }})\right )$ where $c^{\textsf {UID},U_{i}}_{i,F^{\ast }}=(\textsf {vk}_{i}, \sigma _{\textsf {vk}_{i}}, \textsf {UID}, U_{i}, F^{\ast })$ for each i ∈ [N]. Since the forgery satisfies Sig.Verify(mvk $_{i^{\ast }}, \textsf {UID}\|U_{i^{\ast }}\|F^{\ast }\|\textsf {vk}_{i^{\ast }}, \sigma ^{\ast }_{\textsf {vk}_{i^{\ast }}})= 1$, $\mathcal {B}_{\textsf {Sig}}$ outputs $(\textsf {UID}\|U_{i^{\ast }}$$\|F^{\ast }\|\textsf {vk}_{i^{\ast }},\sigma ^{\ast }_{\textsf {vk}_{i^{\ast }}})$ as its message-forgery pair in the security game for the standard signature scheme.

Case 2:b= 0$\mathcal {B}_{\textsf {Sig}}$ guesses that $\mathcal {A}_{\textsf {MA}}$ will produce a Type II forgery:

For each authority i ∈ [N], $\mathcal {B}_{\textsf {Sig}}$ generates Sig.Setup (1^λ) → (msk_i,mvk_i) and sets MSK_i = msk_i and MVK_i = mvk_i. $\mathcal {B}_{\textsf {Sig}}$ forwards mvk_i of all the authorities together with {msk_i} for a specified set S = {i : i ∈ [N]∖i^∗} of corrupted authorities to $\mathcal {A}_{\textsf {MA}}$. $\mathcal {B}_{\textsf {Sig}}$ chooses a random value q^∗ between 1 and Q(λ) as the index of MAFS’s signing queries which the challenge verification key will be positioned on. We use numkeys to denote the number of signing keys that has been generated. We initialize numkeys= 0. As before, $\mathcal {B}_{\textsf {Sig}}$ maintains a dictionary indexed by the tuples $(\textsf {UID}, i^{\ast }, U_{i^{\ast }}^{j}, F)$, whose entries are signing keys that are generated by the authority i^∗ for the user UID with property $U_{i^{\ast }}^{j}$ and policy function F. $\mathcal {B}_{\textsf {Sig}}$ answers the queries issued by $\mathcal {A}_{\textsf {MA}}$ as follows:

• $\textsf {O}_{\textsf {key}}(\textsf {UID}, i^{\ast }, U_{i^{\ast }}^{j}, F):$

  • If there exists an entry for tuple (UID,i^∗, $U_{i^{\ast }}^{j}, F)$ in the dictionary, with value Chal, abort;

  • If there exists an entry for tuple (UID,i^∗, $U_{i^{\ast }}^{j}, F)$ in the dictionary and its value is not Chal, then output the corresponding value $K^{\textsf {UID}, U_{i^{\ast }}^{j}}_{i^{\ast }, F}$.

  • Otherwise, generate (sk_j,vk_j) ←Sig.Setup (1^λ) and $\sigma _{\textsf {vk}_{i^{\ast }}^{j}}\leftarrow \textsf {Sig.Sign}(\textsf {msk}_{i^{\ast }}, \textsf {UID}\|U_{i^{\ast }}$^j∥F∥vk_j). Set $K^{\textsf {UID},U_{i^{\ast }}^{j}}_{i^{\ast }, F}=(\textsf {sk}_{j}, c^{\textsf {UID},U_{i^{\ast }}^{j}}_{i^{\ast },F})$ where $c^{\textsf {UID},U_{i^{\ast }}^{j}}_{i^{\ast },F}=(\textsf {vk}_{j}, \sigma _{\textsf {vk}_{i^{\ast }}^{j}}, \textsf {UID}, U_{i^{\ast }}^{j}, F)$, add it to the dictionary, and output it.

• $\textsf {O}_{\textsf {sign}}(\{\textsf {UID},i^{\ast },U_{i^{\ast }},F\}, \{K^{\textsf {UID},U_{i}}_{i, F}\}\text {} _{i\in [N]\backslash i^{\ast }}, m):$

  • If there exists an entry for tuple $\{\textsf {UID},i^{\ast },U_{i^{\ast }},F\}$ in the dictionary, namely the key $K^{\textsf {UID},U_{i^{\ast }}}_{i^{\ast }, F}$, then it runs (F({(i,U_i)}_i∈[N], m),σ) ←Sign({Ki,F UID,U_i}_i∈[N],m) and outputs the result.

  • If there is no $\{\textsf {UID},i^{\ast },U_{i^{\ast }},F\}$ entry in the dictionary, and numkeys≠q^∗, then $\mathcal {B}_{\textsf {Sig}}$ generates a new key pair of signature scheme, $(\textsf {sk}_{i^{\ast }}, \textsf {vk}_{i^{\ast }})\leftarrow \textsf {Sig.Setup}(1^{\lambda })$, signs $\textsf {UID}\|U_{i^{\ast }}\|F\|\textsf {vk}_{i^{\ast }}$ under $\textsf {msk}_{i^{\ast }}$: $\sigma _{\textsf {vk}_{i^{\ast }}}\leftarrow \textsf {Sig.Sign}(\textsf {msk}_{i^{\ast }},\textsf {UID}\|U_{i^{\ast }}\|F\|\textsf {vk}_{i^{\ast }})$. $\mathcal {B}_{\textsf {Sig}}$ sets $K^{\textsf {UID},U_{i^{\ast }}}_{i^{\ast }, F} :=(\textsf {sk}_{i^{\ast }}, c^{\textsf {UID},U_{i^{\ast }}}_{i^{\ast },F})$ where $c^{\textsf {UID},U_{i^{\ast }}}_{i^{\ast },F}$ = $(\textsf {vk}_{i^{\ast }}, \sigma _{\textsf {vk}_{i^{\ast }}}, \textsf {UID}, U_{i^{\ast }}, F)$, and adds it to the dictionary. For each i ∈ [N], it computes σ_i ←Sig.Sign(sk_i,m) and m^∗ = F({(i,U_i)}_i∈[N],m). Set σ = (m,{ci,F UID,U_i}_i∈[N],{σ_i}_i∈[N]), then output (m^∗,σ). numkeys is then incremented.

  • If there is no $\{\textsf {UID},i^{\ast },U_{i^{\ast }},F\}$ entry in the dictionary and numkeys = q^∗, or if the $\{\textsf {UID},i^{\ast },U_{i^{\ast }},F\}$ entry in the dictionary is set to Chal, then $\mathcal {B}_{\textsf {Sig}}$ sets $\textsf {vk}_{i^{\ast }} :=\textsf {vk}_{\textsf {Sig}}$, signs $\textsf {UID}\|U_{i^{\ast }}\|F\|\textsf {vk}_{\textsf {Sig}}$ under $\textsf {msk}_{i^{\ast }}$: $\sigma _{\textsf {vk}_{i^{\ast }}}\leftarrow \textsf {Sig.Sign}(\textsf {msk}_{i^{\ast }},\textsf {UID}\|U_{i^{\ast }}\|F\|\textsf {vk}_{\textsf {Sig}})$, and queries its oracle for a signature of m under vk_Sig, $\sigma _{i^{\ast }}\leftarrow \textsf {O}_{\textsf {Reg}_{\textsf {sig}}}(m)$. Set $c^{\textsf {UID},U_{i^{\ast }}}_{i^{\ast },F}=(\textsf {vk}_{i^{\ast }}, \sigma _{\textsf {vk}_{i^{\ast }}}, \textsf {UID}, U_{i^{\ast }}, F)$. For each i ∈ [N]∖i^∗ it then runs σ_i ←Sig.Sign(sk_i,m) and m^∗ = F({(i,U_i)}_i∈[N],m). Set σ = (m,{ci,F UID,U_i}_i∈[N],{σ_i}_i∈[N]), then output (m^∗,σ). If there is no $\{\textsf {UID},i^{\ast },U_{i^{\ast }},F\}$ entry in the dictionary, $\mathcal {B}_{\textsf {Sig}}$ sets it to Chal. And numkeys is then incremented.

If $\mathcal {B}_{\textsf {Sig}}$ does not abort, $\mathcal {A}_{\textsf {MA}}$ will output a signature $\left (m^{\ast },\sigma ^{\ast }=(\tilde {m}, \{c^{\textsf {UID},U_{i^{\ast }}}_{i^{\ast },F^{\ast }}, \sigma ^{\ast }_{i^{\ast }}\},\{c^{\textsf {UID},U_{i}}_{i,F^{\ast }},\sigma ^{\ast }_{i}\}\text {} _{i\in [N]\backslash i^{\ast }})\right )$ wh- ere $c^{\textsf {UID},U_{i}}_{i,F^{\ast }}=(\textsf {vk}_{i}, \sigma _{\textsf {vk}_{i}}, \textsf {UID}, U_{i}, F^{\ast })$ for every i ∈ [N]. $\mathcal {B}_{\textsf {Sig}}$ outputs $(\tilde {m},\sigma ^{\ast }_{i^{\ast }})$ as its forgery for the standard signature scheme under vk_Sig.

We will now argue that if $\mathcal {A}_{\textsf {MA}}$ forges in the MAFS scheme with non-negligible probability then $\mathcal {B}_{\textsf {Sig}}$ wins the unforgeability game for the standard signature scheme with non-negligible probability. We note that as long as $\mathcal {A}_{\textsf {MA}}$ doesn’t query the O_key oracle for the secret key corresponding to the embedded vk_Sig challenge, then $\mathcal {B}_{\textsf {Sig}}$ perfectly simulates the O_key and O_sign oracle.

Now, if $\mathcal {A}_{\textsf {MA}}$ produces a Type I forgery, then this forgery must consist of a signature on a new message $\textsf {UID}\|U_{i^{\ast }}\|F^{\ast }\|\textsf {vk}_{i^{\ast }}$ that was not ever signed under the i^∗ authority’s master verification key $\textsf {mvk}_{i^{\ast }}$ during the queries of $\mathcal {A}_{\textsf {MA}}$ to both the oracle O_key and O_sign, which means that $\mathcal {A}_{\textsf {MA}}$ produces a forgery on a new message $\textsf {UID}\|U_{i^{\ast }}\|F^{\ast }\|\textsf {vk}_{i^{\ast }}$ that $\mathcal {B}_{\textsf {Sig}}$ did not query to his signature oracle, which yields a forgery for the standard signature scheme.

If $\mathcal {A}_{\textsf {MA}}$ produces a Type II forgery, by definition the corresponding $\textsf {UID}\|U_{i^{\ast }}\|F^{\ast }\|\textsf {vk}_{i^{\ast }}$ should already have been signed under the i^∗ authority’s master verification key $\textsf {mvk}_{i^{\ast }}$ during the queries of $\mathcal {A}_{\textsf {MA}}$ to both the oracle O_key and O_sign. We declare that the tuple (UID, i^∗, $U_{{i}^{\ast }}$, F^∗) cannot be queried to O_key by $\mathcal {A}_{\textsf {MA}}$, since if it is then given the responded signing key, producing a signature under this signing key is not a valid forgery in the MAFS scheme. Therefore, the tuple (UID, i^∗, ${U}_{{i}^{\ast }}$, F^∗) must then have been issued as a query to O_sign. Namely, the verification key $\textsf {vk}_{i^{\ast }}$ must be freshly generated for a query of form $\textsf {O}_{\textsf {sign}}(\{\textsf {UID},i^{\ast },U_{i^{\ast }},F^{\ast }\}, \{K^{\textsf {UID},U_{i}}_{i, F^{\ast }}\}\text {} _{i\in [N]\backslash i^{\ast }}, m)$ for which no entry under index $(\textsf {UID}, i^{\ast }, U_{i^{\ast }}, F^{\ast })$ previously existed, and then the pair $\textsf {UID}\|U_{i^{\ast }}\|F^{\ast }\|\textsf {vk}_{i^{\ast }}$ was signed under the master signing key of identity i^∗. Note that if $\mathcal {A}_{\textsf {MA}}$ produces a Type II forgery and $\mathcal {B}_{\textsf {Sig}}$ correctly guessed q^∗ where his challenge is embedded in as well as $\mathcal {B}_{\textsf {Sig}}$ does not abort, the forgery produced by $\mathcal {A}_{\textsf {MA}}$ must consist of a signature on a new message $\tilde {m}$ under vk_Sig, for a $\tilde {m}$ that $\mathcal {B}_{\textsf {Sig}}$ has not queried from his own signing oracle, and therefore such a signature also constitutes a forgery for the standard signature scheme.

We note that, if $\mathcal {B}_{\textsf {Sig}}$ does abort, it only can occur when $\mathcal {B}_{\textsf {Sig}}$ did not guess the correct q^∗, since another possible condition of abort occurrence is when $\mathcal {A}_{\textsf {MA}}$ made a query as $\textsf {O}_{\textsf {key}}(\textsf {UID}, i^{\ast }, U_{i^{\ast }}, F^{\ast })$, which is not allowed since if the adversary has queried the $\textsf {O}_{\textsf {key}}(\textsf {UID}, i^{\ast }, U_{i^{\ast }}, F^{\ast })$, no message in the range of F^∗ would be considered a forgery in the MAFS game.

Thus, if $\mathcal {A}_{\textsf {MA}}$ produces a forgery in MAFS scheme with non-negligible probability $\frac {1}{Poly(\lambda )}$, then $\mathcal {B}_{\textsf {Sig}}$ successfully forges in the underlying signature scheme with non-negligible probability $\frac {1}{2Q(\lambda )Poly(\lambda )}$, which contradicts with the assumption that Sig is existentially unforgeable. We conclude that the MAFS scheme as specified above is unforgeable as defined in Section 4. □

5.2 Function-private MAFS from SNARKs

While the construction of MAFS above does not provide function privacy property, in this section we show how to obtain a MAFS scheme satisfying function privacy in the common reference string (CRS) model by employing the building blocks of a FS without function privacy guarantee and a succinct non-interactive argument of knowledge (SNARK). In the CRS model there is an additional setup algorithm, which takes as input the security parameter and outputs the CRS for the system.

As mentioned in the Remark 1, we considered the policy function F consisting of a predicate Predic which is to indicate the set of properties are accepted or not, and a deterministic function f which is to work on the input message. The functionality of policy function $F(\{(id,U_{id})\}\text {} _{(id,U_{id})\in {\Gamma }}, m)$ is first to check $\textsf {Predic}(\{(id, U_{id})\}\text {} _{(id,U_{id})\in {\Gamma }})= 1$, if it is true then output f(m); else output ⊥. In this section, we represent the policy function F as Predic∥f, which means for input $(\{(id,U_{id})\}\text {} _{(id,U_{id})\in {\Gamma }}, m)$, Predic∥f firstly compute $\textsf {Predic}(\{(id,U_{id}) \}\text {} _{(id,U_{id})\in {\Gamma }})$, if the predicate circuit accepts then output f(m), otherwise output ⊥.

Let Sig = (Sig.Setup,Sig.Sign,Sig.Verify) be a signature scheme that is existentially unforgeable under chosen message attacks, FS = (FS.Setup,FS.KeyGen, FS.Sign,FS.Verify) be a FS scheme satisfying the unforgeability but not function privacy, and SNARK=$\left (\textsf {Gen}, \textsf {Prove}, \textsf {Verify}, \mathcal {S}= (\mathcal {S}^{\textsf {crs}}, \mathcal {S}^{\textsf {Proof}}),\textsf {E}=(\textsf {E}_{1}, _{2})\right )$ be a zero knowledge (ZK) SNARK system for the following NP language L:

$$\begin{array}{@{}rcl@{}} L= \{(M, \{\textsf{mvk}\}\text{} _{i\in [N]})|\text{for} & \forall i\in [N],~\exists \sigma_{i}~s.t.~ \\ & \textsf{FS.Verify}(\textsf{mvk}_{i}, M, \sigma_{i})= 1\}. \end{array} $$

By using Sig, FS and SNARK we construct a new MAFS scheme as follows, which also satisfies function privacy.

• Setup(1^λ) :

  • Choose a CRS for the ZK-SNARK: crs ←SNARK.Gen(1^λ).

• ASetup(i,1^λ) :

  • Authority i ∈ [N] samples a pair of keys for Sig: (sk_i,vk_i) ←Sig.Setup(1^λ).

  • Set the master secret key MSK_i = sk_i, and the master verification key MVK_i = vk_i.

• KeyGen(MSK_i,UID,U,Predic∥f) :

  • Parse MSK_i = sk_i and sample a master secret and verification key for the functional signature scheme FS.Setup(1^λ) → (msk_i,mvk_i).

  • Compute η_i ←Sig.Sign(sk_i,UID∥U∥Predic∥mvk_i) and $\textsf {sk}^{f}_{i}\leftarrow \textsf {FS.KeyGen}(\textsf {msk}_{i}, f)$.

  • Create the certificate $c^{\textsf {UID},U}_{i,\textsf {Predic}}=(\eta _{i}, \textsf {UID}, U, \textsf {Predic}, \textsf {mvk}_{i})$.

  • Set $K^{\textsf {UID}, U}_{i,\textsf {Predic}\|f}=(\textsf {sk}^f_{i}, c^{\textsf {UID},U}_{i,\textsf {Predic}})$ and output a key $K^{\textsf {UID}, U}_{i,\textsf {Predic}\|f}$.

• Sign(crs,{Ki,Predic∥f UID,U_i}_i∈[N],m) :

  • Parse $K^{\textsf {UID}, U_{i}}_{i,\textsf {Predic}\|f}=(\textsf {sk}^f_{i}, c^{\textsf {UID},U_{i}}_{i,\textsf {Predic}})$ where ci,PredicUID,U_i = (η_i,UID,U,Predic,mvk_i).

  • For all i ∈ [N] if UID are the same and Predic({(i,U_i)}_i∈[N]) = 1, then run $(f(m),\sigma _{i})\rightarrow \textsf {FS.Sign}(\textsf {sk}^{f}_{i}, m)$.

  • Run π_i ←SNARK.Prove ((f(m),{mvk_i}_i∈[N]),{σ_i}_i∈[N],crs), a ZK-SNARK that (f(m),{mvk_i}_i∈[N]) ∈ L, where L is defined as above.

  • Set m^∗ = f(m) and σ = ({ci,PredicUID,U_i}_i∈[N],π).

  • Output (m^∗,σ).

• Verify(crs,{MVK_i}_i∈[N],m^∗,σ) :

  • Parse MVK_i = vk_i and σ = ({ci,PredicUID,U_i}_i∈[N],π) where ci,PredicUID,U_i = (η_i,UID,U,Predic,mvk_i), and perform the following checks. If all of the checks pass output 1; otherwise output 0.

    • 1. UID are the same and Predic({(i,U_i)}_i∈[N]) = 1;

    • 2. Sig.Verify(vk_i,UID∥U∥Predic∥mvk_i,η_i) = 1for all i ∈ [N];

    • 3. SNARK.Verify(crs,({mvk_i}_i∈[N],m^∗),π) = 1.

Theorem 4

Assume the existence of functional signature schemeFSsupporting theclass$\mathcal {F}$ofpolynomial-sized circuits that satisfies unforgeability but not function privacy,Sig is an existentially unforgeable signature scheme, andSNARKbe an adaptive zero-knowledge SNARK system forNP. Then, there exists a MAFS scheme as specified above, which satisfies both the unforgeability (Definition4)and function privacy (Definition 5).

Proof

We first prove that our scheme satisfies unforgeability. Let us fix a PPT adversary $\mathcal {A}_{\textsf {MA}}$. We will use $\mathcal {A}_{\textsf {MA}}$ to construct an adversary $\mathcal {B}$ such that, if $\mathcal {A}_{\textsf {MA}}$ wins in the unforgeability game for multi-authority functional signatures with non-negligible probability, then $\mathcal {B}$ either breaks the underlying signature scheme or functional signature scheme, which are assumed to be secure.

$\mathcal {B}$ interacts with $\mathcal {A}_{\textsf {MA}}$, playing the role of the challenger in the security game for the multi-authority functional signature scheme. $\mathcal {B}$ generates (crs,trap) ←E₁(1^λ), a simulated CRS for the ZK-SNARK, together with a trapdoor, and forwards crs to $\mathcal {A}_{\textsf {MA}}$ as the CRS. $\mathcal {B}$ also must simulate the O_key and O_sign oracles. $\mathcal {B}$ flips a coin b, indicating his guess for the type of forgery $\mathcal {A}_{\textsf {MA}}$ will produce, and places his challenge accordingly. Since $\mathcal {B}$ behaves almost the same as what he does in Case 1 and Case 2 of the proof in Theorem 3. We omit the details here. Eventually $\mathcal {A}_{\textsf {MA}}$ outputs a forgery $\left (m^{\ast },\sigma ^{\ast }=(\{c^{\textsf {UID},U_{i}}_{i,\textsf {Predic}^{\ast }}\}\text {} _{i\in [N]}, \pi ^{\ast })\right )$ where $c^{\textsf {UID},U_{i}}_{i,\textsf {Predic}^{\ast }}=(\eta ^{\ast }_{i}, \textsf {UID}, U_{i}, \textsf {Pre-} \textsf {dic}^{\ast }, \textsf {mvk}_{i})$ such that:

• π^∗ is a valid proof the statement ({mvk_i}_i∈[N],m^∗) ∈ L under CRS;

• For each $i\in \bar {S}$, $\eta ^{\ast }_{i}$ is a valid signature of UID∥U_i∥Pre-dic^∗∥mvk_i under vk_i;

• $\mathcal {A}_{\textsf {MA}}$ has not sent a query of form $\left (\{\textsf {UID},i, U_{i}, \textsf {Predic}^{\ast } \|\tilde {f}\}\text {} _{i\in \bar {S}}, \{K^{\textsf {UID},U_{i}}_{i,\textsf {Predic}^{\ast }\|\tilde {f}}\}\text {} _{i\in S}, \tilde {m}\right )$ to the signing oracle O_sign for any $\tilde {f}$ and $\tilde {m}$ such that $\tilde {f}(\tilde {m})=m^{\ast }$.

• $\mathcal {A}_{\textsf {MA}}$ has not sent queries $(\textsf {UID}, i, U_{i}, \textsf {Predic}^{\ast }\|\tilde {f})$ for all $i \in \bar {S}$, to the oracle O_key such that the user UID’s property set {(i,U_i)}_i∈[N] is accepted by Predic^∗ and for any $\tilde {f}$ that has m^∗ in its range.

In Case 1, $\mathcal {B}$ finally outputs $(\textsf {UID}\|U_{i^{\ast }}\|$$\textsf {Predic}^{\ast }\|\textsf {mvk}_{i^{\ast }}, \eta ^{\ast }_{i^{\ast }})$ as its message-forgery pair for the standard signature scheme. Whereas, in Case 2, $\mathcal {B}$ runs the extractor E₂(crs,trap,(m^∗,{mvk_i}_i∈[N]),π^∗) to recover a witness $w=\{\sigma ^{\ast }_{i}\}\text {} _{i\in [N]}$ such that $\textsf {FS.Verify}(\textsf {mvk}_{i},m^{\ast }, \sigma ^{\ast }_{i})= 1$ for all i ∈ [N]. $\mathcal {B}$ then outputs $(m^{\ast },\sigma ^{\ast }_{i^{\ast }})$ as a forgery for the FS scheme under mvk_FS.

We will now argue that if $\mathcal {A}_{\textsf {MA}}$ forges the MAFS scheme with non-negligible probability, then $\mathcal {B}$ either wins the unforgeability game for the standard signature scheme or the functional signature with non-negligible probability.

Hybrid 0 The real MAFS challenge experiment. Namely, the CRS is generated in the honest manner crs ←SNARK.Gen(1^λ). Let Forge₀ denote the probability of the adversary producing a valid forgery in the MAFS scheme in this game.

Hybrid 1 The same experiment as Hybrid 0, except that the CRS is generated using the extractor, (crs,trap) ←E₁(1^λ). Let Forge₁ denote the probability of the adversary producing a valid forgery in a MAFS scheme in this game. Following directly from the fact that the CRS values generated via the standard algorithm Gen and those generated by the extractor algorithm E₁ are statistically close, we have Forge₁ −Forge₀ ≤ negl(λ).

Hybrid 2 The same experiment as Hybrid 1. And at the end we apply the ZK-SNARK extraction algorithm on the adversary’s forgery $\sigma ^{\ast }=(\{c^{\textsf {UID},U_{i}}_{i,\textsf {Predic}^{\ast }}\}\text {} _{i\in [N]}, \pi ^{\ast })$ (on message m^∗) in the MAFS scheme: i.e., $\textsf {E}_{2}(\textsf {crs}, \textsf {trap}, (m^{\ast }, \{\textsf {mvk}_{i}\}\text {} _{i\in [N]}), \pi ^{\ast })\rightarrow \{\sigma ^{\ast }_{i}\}\text {} _{i\in [N]}$. Let Forge₂ denote the probability that $\sigma ^{\ast }_{i^{\ast }}$ is a valid signature in the underlying FS scheme on a message m^∗. Following directly from the extraction property of the ZK-SNARK system, we have Forge₂ −Forge₁ ≤ negl(λ).

Since Forge₂ is precisely the probability that the adversary $\mathcal {B}$ constructed above produces a successful forgery in the unforgeability game for FS, due to the unforgeability of FS, we have Forge₂ ≤ negl(λ).

To prove that our scheme satisfies function privacy, we show that if there exists a PPT adversary $\mathcal {A}_{\textsf {priv}}$ wining the function privacy game for MAFS with non-negligible advantage, then there exists an PPT adversary breaking the zero knowledge security game of the ZK-SNARK. More specifically, consider the following two hybrid games:

Hybrid 0 The real function privacy game. Namely, the CRS for the ZK-SNARK system is honestly generated crs ←SNARK.Gen(1^λ). To generate the challenge signature on message m_b for a random bit b ∈{0,1}, the challenger first generates a signature on m_b under the underlying FS scheme: $({f}_{b}({m}_{b}),\sigma _{i})\rightarrow \textsf {FS.Sign}(\textsf {sk}^{{f}_{b}}_{i}, m_b)$ for each i ∈ [N] and then honestly generates a proof π ←SNARK.Prove ((f_b(m_b),{mvk_i}_i∈[N]),{σ_i}_i∈[N],crs).

Hybrid 1 The same game as Hybrid 0 except that the proof in the challenge signature is generated in the simulated manner. Namely, the CRS is generated using the simulator algorithm $(\textsf {crs}, \textsf {trap})\leftarrow \mathcal {S}^{\textsf {crs}}(1^{\lambda })$. The challenger then uses the simulator to generate the proof $\pi \leftarrow \mathcal {S}^{\textsf {Proof}}((\textsf {crs}, \textsf {trap}),(m^{\ast }, \{\textsf {mvk}_{i}\}\text {} _{i\in [N]}))$, where m^∗ = f₀(m₀) = f₁(m₁).

Following directly from the zero knowledge property of the ZK-SNARK system, the difference between the advantage of the adversary $\mathcal {A}_{\textsf {priv}}$ in guessing the bit b in Hybrid 0 and Hybrid 1 is negligible. Note that the view of $\mathcal {A}_{\textsf {priv}}$ in Hybrid 1 is independent with the bit b, hence any PPT adversary cannot correctly guess the bit b with non-negligible advantage. □

6 Conclusion

The emergence of the IoT, has led to millions of sensors and smart devices sending sensitive data across communication networks. Thus, it is of utmost importance to address the challenge of guaranteeing the integrity and authentication of the transmitted information. To achieve that we propose a generalized signature scheme with a fine grained access control, that can provide significant advantages to the digital world, in application settings where the authenticity of shared information is crucial e.g., smart healthcare, smart homes, smart cities. In this paper, we introduce the definition of multi-authority functional signatures (MAFSs) for general policy functions, and provide a general transformation from a standard signature scheme to a MAFS scheme satisfying unforgeability property but not function privacy. Given a non-function-private functional signature and a SNARK we provide a way to build a function private MAFS scheme.

Our MAFS can properly solve the problem we depicted in the IoT related delivery operation world and successfully provides both businesses and customers greater visibility and trackability of their products and parcels than ever before. In particular, by using our MAFS the records of all transactions during the en-route of delivery is able to be kept and renewed. Moreover, we allow the multiple authorities to be involved in the execution of the transactions, meanwhile ensuring that the users are able to verify all the transactions occurred in the network. We believe our MAFS can be applied to other IoT related application scenarios.

Appendices

Appendix A: Signature scheme

Definition 7

A signature scheme with message space $\mathcal {M}(\lambda )$, signature key space $\mathcal {SK}(\lambda )$ and verification key space $\mathcal {VK}(\lambda )$ consists of the PPT algorithms (SIG.Setup,SIG.Sign,SIG.Verify):

• Key generation.SIG.Setup is a randomized algorithm that takes as input the security parameter 1^λ and outputs the signing key $\textsf {sk}\in \mathcal {SK}$ and the verification key $\textsf {vk}\in \mathcal {VK}$.

• Signature generation.SIG.Sign takes as input the signing key $\textsf {sk}\in \mathcal {SK}$ and a message $m\in \mathcal {M}$ and outputs a signature σ.

• Verification.SIG.Verify takes as input a verification key $\textsf {vk}\in \mathcal {VK}$, a message $m\in \mathcal {M}$ and a signature σ and outputs either 0 or 1.

Correctness For all $\lambda \in \mathbb {N}$, (vk,sk) ←SIG.Setup(1^λ), messages $m\in \mathcal {M}(\lambda )$, we require that

$$\textsf{SIG.Verify}(\textsf{vk},m, \textsf{SIG.Sign}(\textsf{sk},m))= 1.$$

We say that a signature scheme SIG = (SIG.Setup,SIG.Sign,SIG.Verify) is existentially unforgeable under adaptively chosen message attacks if

$$\text{Pr}[\textsf{Exp}^{\textsf{uf-cma}}_{\textsf{SIG},\mathcal{A}}(\lambda)= 1]\leq negl(\lambda) $$

for some negligible function negl() and for all PPT attackers $\mathcal {A}$, where $\textsf {Exp}^{\textsf {uf-cma}}_{\textsf {SIG},\mathcal {A}}(\lambda )$ is the following experiment with the scheme SIG and an attacker $\mathcal {A}$:

• 1. (vk,sk) ←SIG.Setup(1^λ).

• 2. $(m^{\ast },\sigma ^{\ast })\leftarrow \mathcal {A}^{\textsf {Sign}(\textsf {sk},\cdot )}(1^{\lambda },\textsf {vk})$. If SIG.Verify(vk,m^∗,σ^∗) = 1 and m^∗ was not queried to the Sign(sk,⋅) oracle, then return 1, else return 0.

Appendix B: Succinct Non-Interactive Arguments (SNARGs)

We employ the definition of SNARGs in [2].

Definition 8

π = (Gen,Prove,Verify) is a succinct non-intera- ctive argument for a language L ∈NP with witness relation R if it satisfies the following properties:

• Completeness: For all x,w such that R(x,w) = 1, and for all strings crs ←Gen(1^k), Verify(crs,x,Prove(x,w,crs)) = 1.

• Adaptive Soundness: There exists a negligible function μ(k), such that, for all PPT adversaries $\mathcal {A}$, if crs ←Gen(1^k) is sampled uniformly at random, then the probability that $\mathcal {A}(\textsf {crs})$ will output a pair (x,π) such that x∉L and yet Verify(crs,x,π) = 1, is at most μ(k).

• Succinctness: There exists an universal polynomial p(k) that does not depend on the relation R, such that ∀x,ws.tR(x,w) = 1,crs ←Gen(1^k),π ←Prove(x,w,crs),

  $$|\pi| \leq p(k + \log R)$$

  where R denotes the runtime of the relation associated with language L.

Definition 9

A SNARG π = (Gen,Prove,Verify) is a succinct non-interactive argument of knowledge(SNARK) for a language L ∈NP with witness relation R if there exists a negligible function μ(⋅) such that, for all PPT provers P^∗, there exists a PPT algorithm $\textsf {E}_{P^{\ast }}= (\textsf {E}^{1}_{P^{\ast }}, \textsf {E}^2_{P^{\ast }})$ such that for every adversary A,

$$\begin{array}{@{}rcl@{}} |\text{Pr}[\mathcal{A}(\textsf{crs}) \rightarrow 1\ |& \textsf{crs} \leftarrow \textsf{Gen}(1^{k})]- \\ & \text{Pr}[\mathcal{A}(\textsf{crs})\rightarrow 1|(\textsf{crs}, \textsf{trap})\leftarrow \textsf{E}^{1}_{P^{\ast}}(1^{k})]|=\mu(k), \end{array} $$

and,

$$\begin{array}{@{}rcl@{}} \text{Pr}[P^{\ast}(\textsf{crs})& \rightarrow (x, \pi)~\text{and}~\textsf{E}^{2}_{P^{\ast}}(\textsf{crs}, \textsf{trap}, x, \pi)\rightarrow w^{\ast}~ \\ & s.t. ~\textsf{Verify}(\textsf{crs}, x, \pi)\rightarrow 1~\text{and} ~(x,w^{\ast})\notin R]= \mu(k). \end{array} $$

where the probabilities are taken over $(\textsf {crs}, \textsf {trap})\leftarrow \textsf {E}^{1}_{P^{\ast }}(1^k)$, and over the random coin tosses of the extractor algorithm $\textsf {E}^2_{P^{\ast }}$.

Definition 10

A SNARK π = (Gen,Prove,Verify) is a zero-knowledge SNARK for a language L ∈NP with witness relation R if there exist PPT algorithms $S = (\mathcal {S}^{\textsf {crs}}, \mathcal {S}^{\textsf {Proof}})$ satisfying the following property:

• Adaptive Zero-Knowledge: For all PPT adversaries $\mathcal {A}$,

  $$|\text{Pr}[\text{Exp}_{\mathcal{A}}(k)\rightarrow 1]-\text{Pr}[\text{Exp}^{S}_{\mathcal{A}}(k)\rightarrow 1]|\leq \mu(k), $$

  where the experiments $\text {Exp}_{\mathcal {A}}(k)$ and $\text {Exp}^{S}_{\mathcal {A}}(k)$ are defined as follows:

  

  where $S^{\prime }(\textsf {crs}, \textsf {trap}, x, w) = \mathcal {S}^{\textsf {Proof}}(\textsf {crs}, \textsf {trap}, x)$.